8.3 Posterior hypothesis testing

Hypothesis testing:

$$H_0: \pi \geqslant 0.2$$ $$H_a: \pi < 0.2$$

One-sided tests

To evaluate exactly how plausible it is that $\pi<0.2$:

• calculate the posterior probability

$$P(\pi < 0.2|Y=14)$$

pbeta(0.20, 18, 92)

## [1] 0.8489856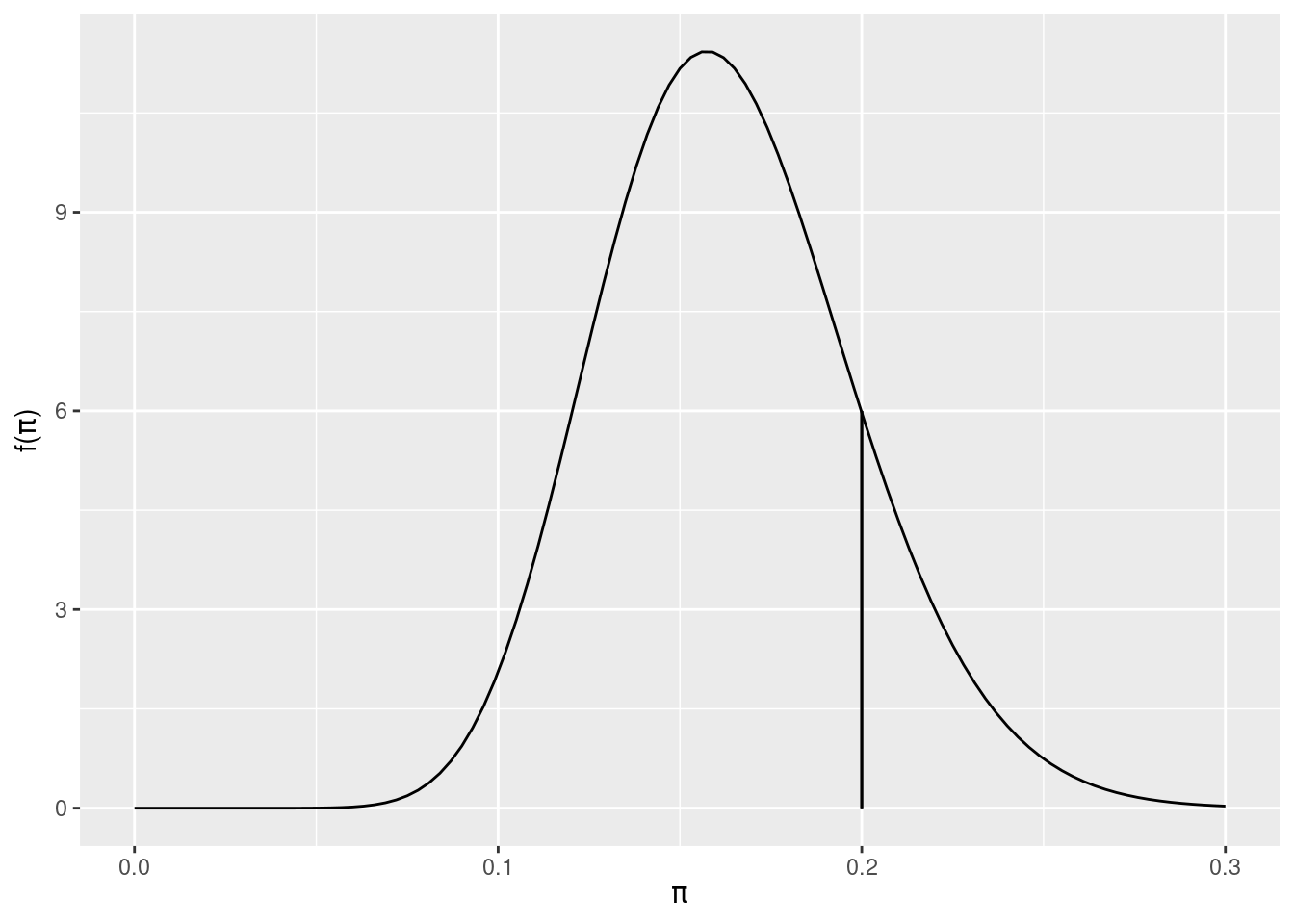

$$P(H_0|Y=14)=0.151$$ $$P(H_a|Y=14)=0.849$$

$$\text{posterior odds}=\frac{P(H_a|Y=14)}{P(H_0|Y=14)} \approx 5.62$$

pbeta(0.20, 18, 92) / (1 - pbeta(0.20, 18, 92))

## [1] 5.621883

$$\text{prior odds}=\frac{P(H_a)}{P(H_0)} \approx 0.093$$

pbeta(0.20, 4, 6) / (1 - pbeta(0.20, 4, 6))

## [1] 0.09366321

$$\text{Bayes Factor}=\frac{\text{posterio odds}}{\text{prior odds}}$$

BF <- (pbeta(0.20, 18, 92) / (1 - pbeta(0.20, 18, 92))) / (pbeta(0.20, 4, 6) / (1 - pbeta(0.20, 4, 6)))
BF

## [1] 60.02232

$$BF=\left\{\begin{matrix} 1 & H_a\text{constant} \\ >1 & H_a\text{increased} \\ <1 & H_a\text{decreased} \\ \end{matrix}\right.$$

Two-sided tests

There’s not one recipe for success

$$H_0: \pi = 0.3$$ $$H_a: \pi \neq 0.3$$