18.2 Hierarchical logistic regression

# Load packages
library(bayesrules)
library(tidyverse)
library(bayesplot)
library(rstanarm)
library(tidybayes)
library(broom.mixed)
library(janitor)

climbers <- climbers_sub %>% 
  select(expedition_id, member_id, success, year, season,
         age, expedition_role, oxygen_used)

Data are from The Himalayan Database, Himalayan Climbing Expeditions data shared through the #tidytuesday project R for Data Science 2020b, made of 2076 climbers, dating back to 1978.

# Import, rename, & clean data
data(climbers_sub)
climbers <- climbers_sub %>% 
  select(expedition_id, member_id, success, year, season,
         age, expedition_role, oxygen_used)
nrow(climbers)

## [1] 2076

climbers%>%head

# A tibble: 6 × 8
  expedition_id member_id success  year season   age expedition_role oxygen_used
  <chr>         <fct>     <lgl>   <dbl> <fct>  <dbl> <fct>           <lgl>      
1 AMAD81101     AMAD8110… TRUE     1981 Spring    28 Climber         FALSE      
2 AMAD81101     AMAD8110… TRUE     1981 Spring    27 Exp Doctor      FALSE      
3 AMAD81101     AMAD8110… TRUE     1981 Spring    35 Deputy Leader   FALSE      
4 AMAD81101     AMAD8110… TRUE     1981 Spring    37 Climber         FALSE      
5 AMAD81101     AMAD8110… TRUE     1981 Spring    43 Climber         FALSE      
6 AMAD81101     AMAD8110… FALSE    1981 Spring    38 Climber         FALSE      

To generate a frequency table we use the tabyl() function:

?janitor::tabyl

climbers %>% 
  janitor::tabyl(success)

 success    n   percent
   FALSE 1269 0.6112717
    TRUE  807 0.3887283

# Size per expedition
climbers_per_expedition <- climbers %>% count(expedition_id)

# Number of expeditions
nrow(climbers_per_expedition)

## [1] 200

The individual climber outcomes are independent.

climbers_per_expedition %>% 
  head(3)

## # A tibble: 3 × 2
##   expedition_id     n
##   <chr>         <int>
## 1 AMAD03107         5
## 2 AMAD03327         6
## 3 AMAD05338        12

More than 75 of our 200 expeditions had a 0% success rate. In contrast, nearly 20 expeditions had a 100% success rate.

There’s quite a bit of variability in expedition success rates.

# Calculate the success rate for each exhibition
expedition_success <- climbers %>% 
  group_by(expedition_id) %>% 
  summarize(success_rate = mean(success))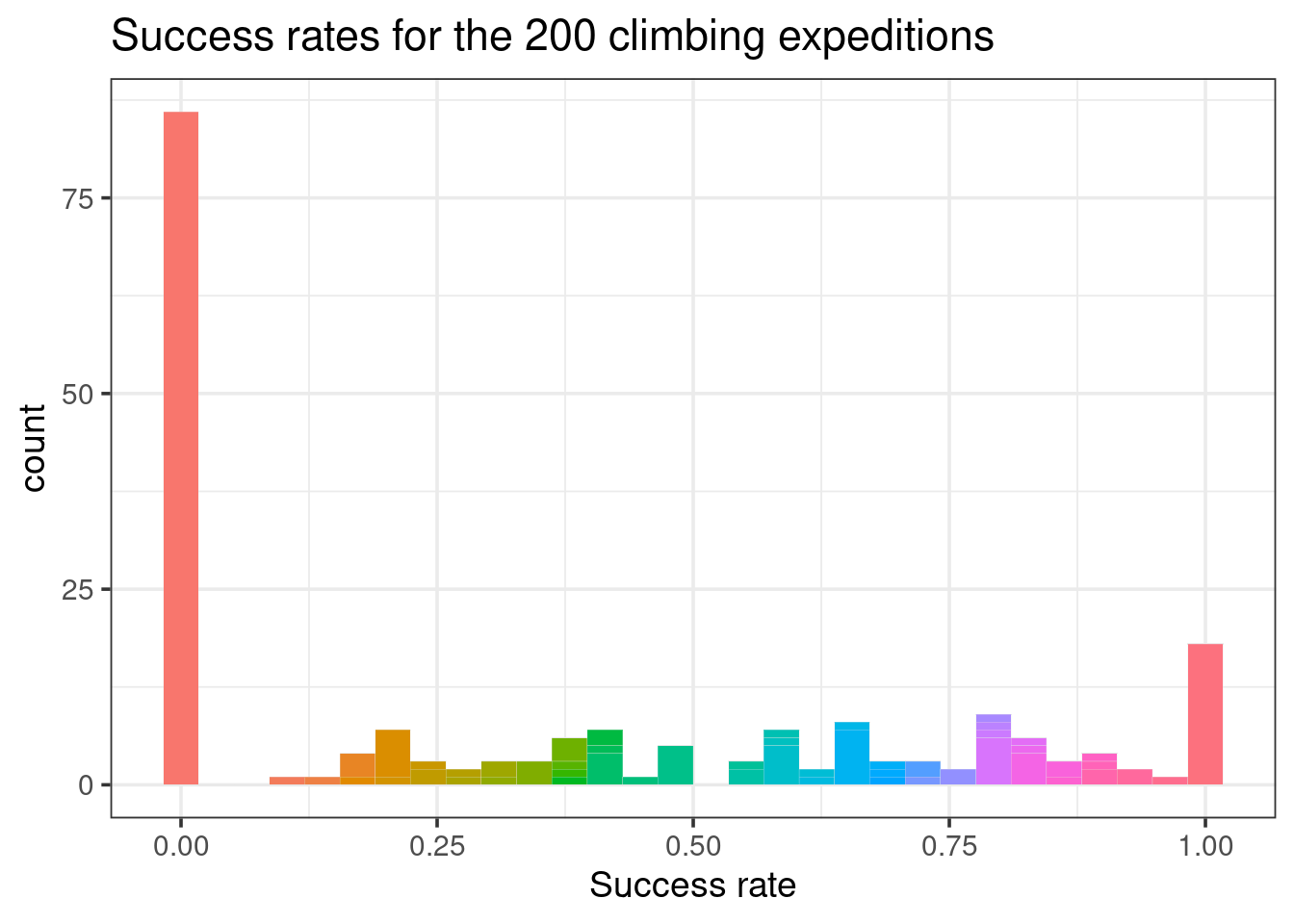

Figure 18.2: Histogram of the success rates for the 200 climbing expeditions

18.2.1 Model building & simulation

We use the Bernoulli model for binary response variable: expedtion success

$$Y_{ij}=\left\{\begin{matrix} 0 & \text{yes} \\ 1 & \text{no} \end{matrix}\right.$$

$$X_{ij1}= \text{age of climber j in expedition j}$$ $$X_{ij2}= \text{climber i received oxygen in expedition j}$$

Bayesian model

$$Y_{ij}|\pi_{ij}\sim Bern(\pi_{ij})$$ Complete pooling expands this simple model into a logistic regression model

$$Y_{ij}|\beta_0,\beta_1,\beta_2\overset{ind}\sim Bern(\pi_{ij})$$

with

• $\beta_0$ the typical baseline success rate across all expeditions
• $\beta_1$ the global relationship between success and age when controlling for oxygen use
• $\beta_2$ the global relationship between success and oxygen use when **controlling for age

$$log(\frac{\pi_{ij}}{1-\pi_{ij}})=\beta_0+\beta_1X_{ij1}+\beta_2X_{ij2}$$ We need to take account for the grouping structure of our data.

# Calculate the success rate by age and oxygen use
data_by_age_oxygen <- climbers %>% 
  group_by(age, oxygen_used) %>% 
  summarize(success_rate = mean(success),.groups="drop")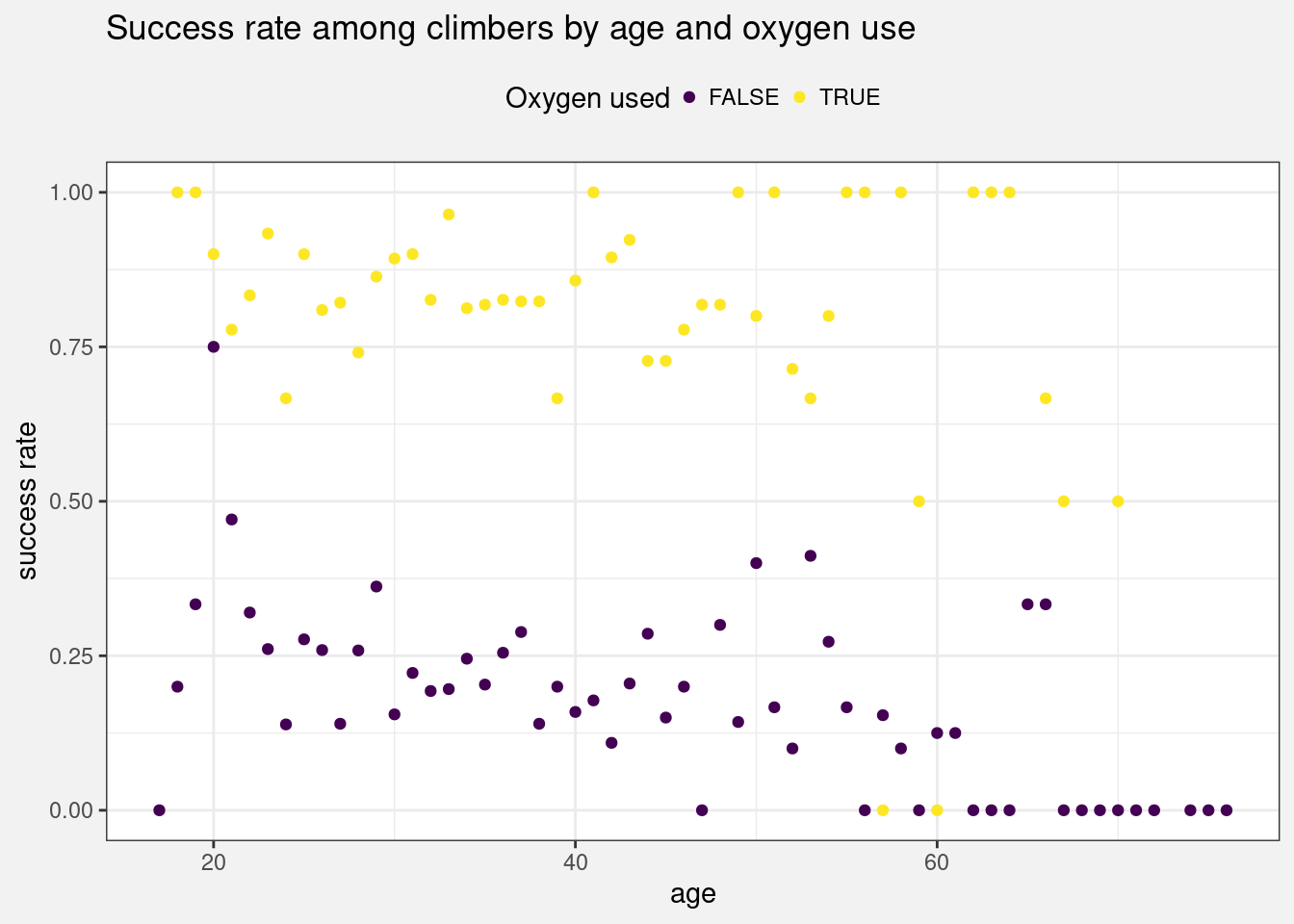

Figure 18.3: Scatterplot of the success rate among climbers by age and oxygen use

We substitute $\beta_0$ with the centered intercept $\beta_{0c}$.

$$\beta_{0c}\sim N(m_0,s_0^2)$$

$m_0=0$ and $s_0^2=2.5^2$, $s_1^2=0.24^2$, $s_2^2=5.51^2$

$$\beta_{0j}|\beta_0,\sigma_0\overset{ind}\sim N(\beta_0,s_0^2)$$

and,

$$\sigma_0\sim Exp(1)$$

Reframe the random intercepts logistic regression model as a tweaks to the global intercept:

$$log(\frac{\pi_{ij}}{1-\pi_{ij}})=(\beta_0+b_{0j})+\beta_1X_{ij1}+\beta_2X_{ij2}$$

• $b_{0j}$ depends on the variability

$$b_{0j}|\sigma_0\overset{ind}\sim N(0,\sigma_0^2)$$

• $\sigma_0$ captures the between-group variability in success rates from expedition to expedition

Set the model formula to hierarchical grouping structure:

success ~ age + oxygen_used + (1 | expedition_id)

climb_model <- stan_glmer(
  success ~ age + oxygen_used + (1 | expedition_id), 
  data = climbers, family = binomial,
  prior_intercept = normal(0, 2.5, autoscale = TRUE),
  prior = normal(0, 2.5, autoscale = TRUE), 
  prior_covariance = decov(reg = 1, conc = 1, shape = 1, scale = 1),
  chains = 4, iter = 5000*2, seed = 84735
)

Confirm prior specifications

prior_summary(climb_model)

MCMC diagnostics

mcmc_trace(climb_model, size = 0.1)
mcmc_dens_overlay(climb_model)
mcmc_acf(climb_model)
neff_ratio(climb_model)
rhat(climb_model)

Define success rate function

success_rate <- function(x){mean(x == 1)}

Posterior predictive check

pp_check(climb_model, nreps = 100,
         plotfun = "stat", stat = "success_rate") + 
  xlab("success rate")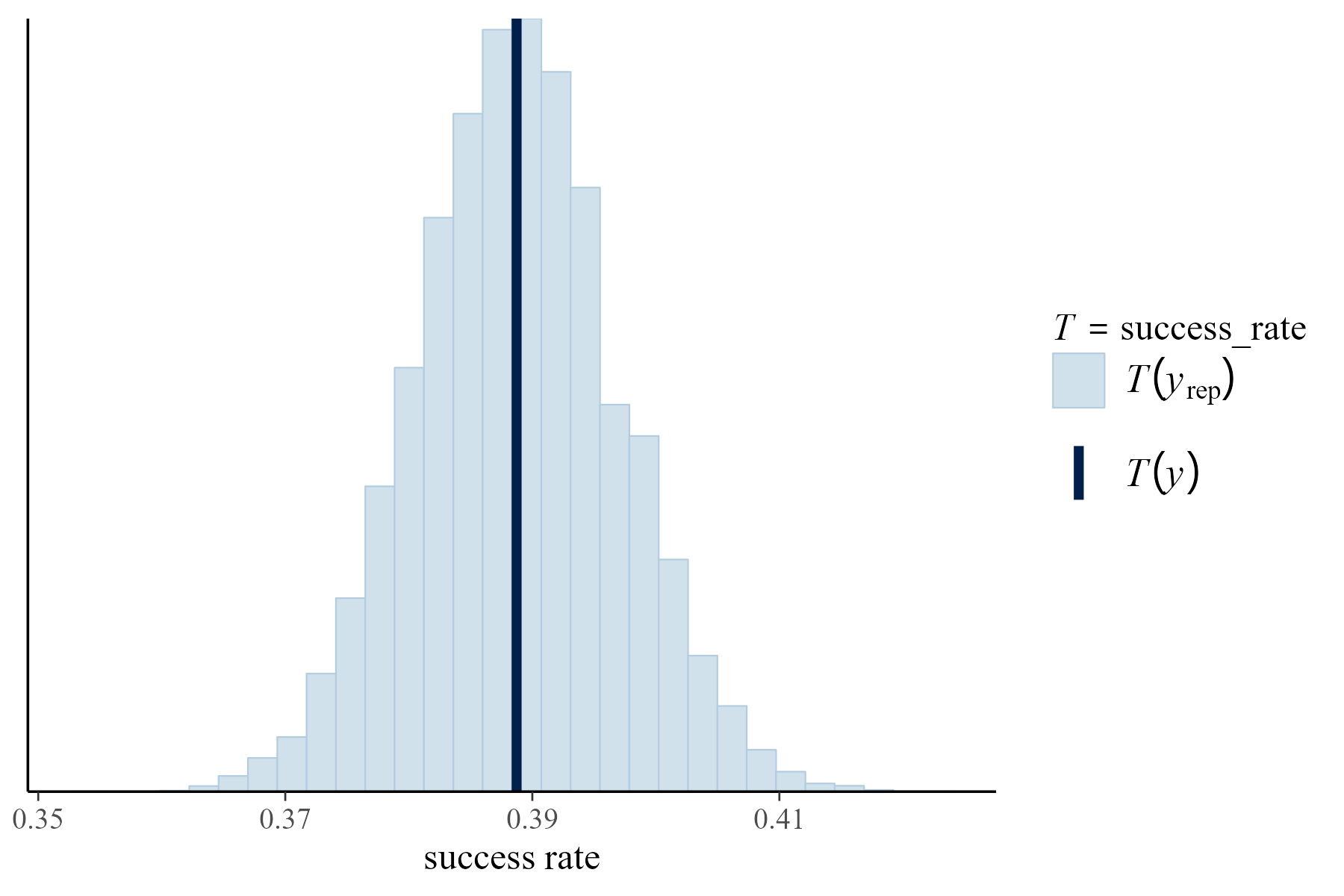

(#fig:18-pp_check_fig)The histogram displays the proportion of climbers that were successful in each of 100 posterior simulated datasets

18.2.2 Posterior analysis

Posterior summaries for our global regression parameters reveal that the likelihood of success decreases with age.

tidy(climb_model, 
     effects = "fixed",
     conf.int = TRUE, 
     conf.level = 0.80)

Confidence intervals are expressed as the log(odds) to the odds scale, so will be converted to:

$$(e^{-conf.low},e^{-conf.high})=(a,b)$$

On the probability of success scale

$$\pi=\frac{e^{-\beta_0-\beta_1X_1+\beta_2X_2}}{1+e^{-\beta_0-\beta_1X_1+\beta_2X_2}}$$

Results are: both with oxygen and without, the probability of success decreases with age.

climbers %>%
  add_fitted_draws(climb_model, n = 100, re_formula = NA) %>%
  ggplot(aes(x = age, y = success, color = oxygen_used)) +
    geom_line(aes(y = .value, group = paste(oxygen_used, .draw)), 
              alpha = 0.1) + 
    labs(y = "probability of success")

18.2.3 Posterior classification

New expedition

new_expedition <- data.frame(
  age = c(20, 20, 60, 60), oxygen_used = c(FALSE, TRUE, FALSE, TRUE), 
  expedition_id = rep("new", 4))

new_expedition

##   age oxygen_used expedition_id
## 1  20       FALSE           new
## 2  20        TRUE           new
## 3  60       FALSE           new
## 4  60        TRUE           new

Posterior predictions of binary outcome

set.seed(84735)
binary_prediction <- posterior_predict(climb_model, newdata = new_expedition)

# First 3 prediction sets
head(binary_prediction, 3)

##      1 2 3 4
## [1,] 0 1 0 1
## [2,] 0 1 0 0
## [3,] 0 1 0 1

Summarize the posterior predictions of Y

colMeans(binary_prediction)

##       1       2       3       4 
## 0.28470 0.80185 0.14755 0.64565

18.2.4 Model evaluation

set.seed(84735)
classification_summary(data = climbers, model = climb_model, cutoff = 0.5)
set.seed(84735)
classification_summary(data = climbers, model = climb_model, cutoff = 0.65)