17.4 Hierarchical model with varying intercepts & slopes

ggplot(running, aes(x = age, y = net, group = runner)) + 
  geom_smooth(method = "lm", se = FALSE, size = 0.5)

## `geom_smooth()` using formula = 'y ~ x'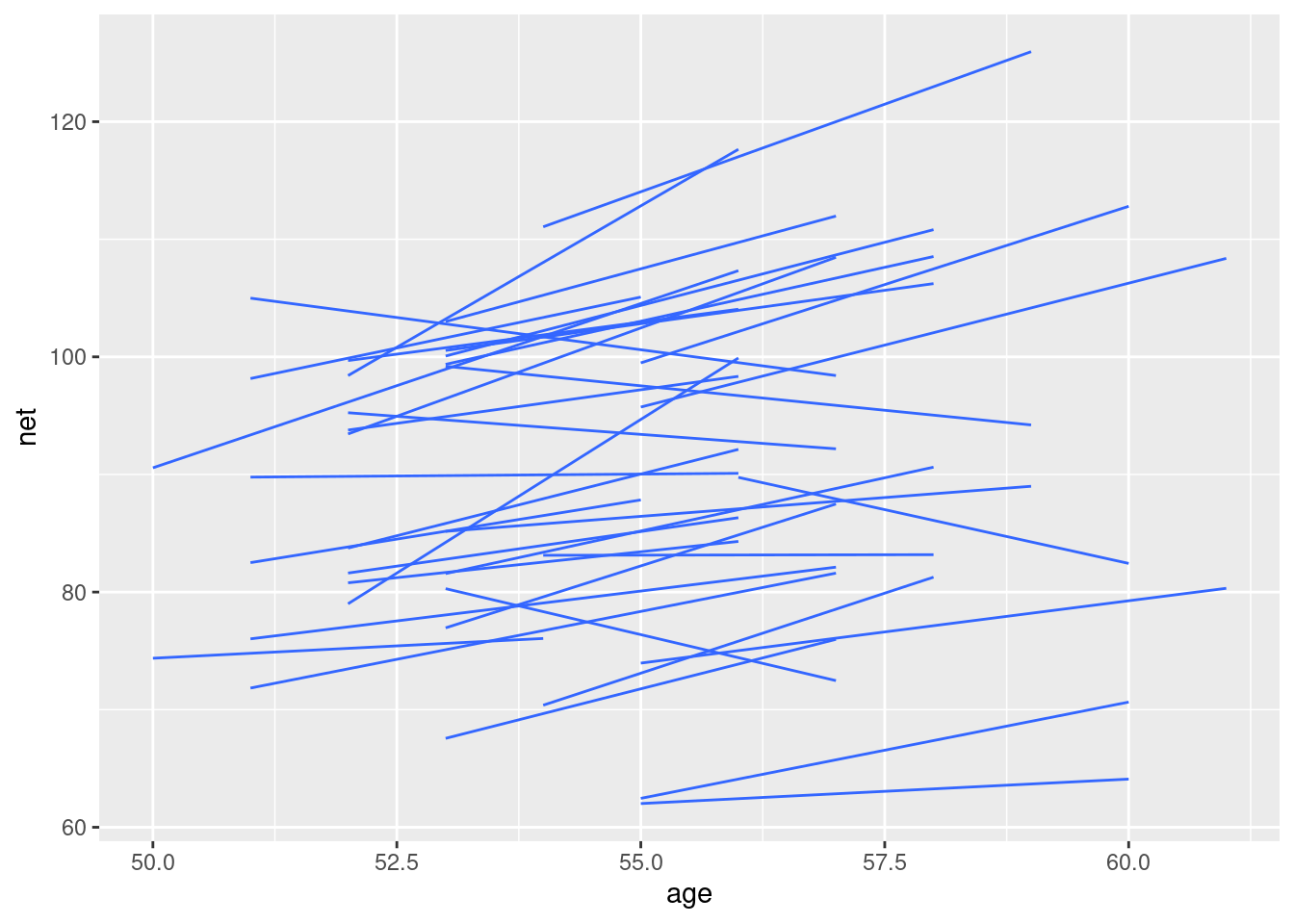

Quiz!

source:thebrain187

How can we modify our random intercepts models to recognize that the rate at which running time change with age might vary from runner to runner?

17.4.1 Model building

$$Y_{ij} | \beta_{0j}, \beta_{1j}, \sigma_y \sim N(\mu_{ij}, \sigma_y^2)$$

$$\mu_{ij} = \beta_{0j} + \beta_{1j}X_{ij}$$

$$\beta_{0j} | \beta_{0}, \sigma_0 \sim N(\beta_0, \sigma_0^2)$$

$$\beta_{1j} | \beta_{1}, \sigma_1 \sim N(\beta_1, \sigma_1^2)$$ But $\beta_{0j}$ and $\beta_{1j}$ are correlated for runner j. Let $\rho \in [-1,1]$ represent the correlation between $\beta_{0j}$ and $\beta_(1j)$. We will need to do a joint Normal model of both:

$$\begin{pmatrix} \beta_{0j} \\ \beta_{1j} \end{pmatrix} | \beta_0, \beta_1, \sigma_0, \sigma_1 \sim N \begin{pmatrix}\begin{pmatrix} \beta_0 \\ \beta_1 \end{pmatrix}, \Sigma \end{pmatrix}$$

$$\Sigma = \begin{pmatrix} \sigma_0² & \rho\sigma_0\sigma_1 \\ \rho\sigma_0\sigma_1 & \sigma_1^2 \end{pmatrix}$$

$\Sigma$ is our covariance matrix

Let me google it for you:

$$\rho(X,Y) = \frac{Cov(X,Y)}{\sigma_X\sigma_y} \in [-1, 1]$$

Examples:

• strong negative correlation between $\beta_{0j}$ and $\beta_{1j}$ with small intercept: smaller you start higher you go

• strong positive correlation with small intercept : smaller you start lower you go

• no correlation : X and Y do their life

Quiz!

1. $\beta_{0j}$ and $\beta_{1j}$ are negatively correlated:

1. Runners that start out slower (i.e., with a higher baseline), also tend to slow down at a more rapid rate.
2. The rate at which runners slow down over time isn’t associated with how fast they start out.
3. Runners that start out faster (i.e., with a lower baseline), tend to slow down at a more rapid rate.

2. $\beta_{0j}$ and $\beta_{1j}$ are positively correlated:

If $\sigma_1 = 0$, age will not differ group to group we are back to the random intercepts model.

But how do we get our Joint prior model?

We are using a decomposition of covariance model and the function decov() (rememver the prior_covariance = decov(reg = 1, conc = 1, shape = 1, scale = 1) in our stan_glmer call)

We can decompose our matrix in 3 components:

$$R = \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix}$$

$$\tau = \sqrt{\sigma^2_0 + \sigma^2_1}$$

$$\pi = \begin{pmatrix} \pi_0 \\ \pi_1 \end{pmatrix} = \begin{pmatrix}\frac{\sigma_0^2}{\sigma_0^2 + \sigma_1^2} \\ \frac{\sigma_1^2}{\sigma_0^2 + \sigma_1^2} \end{pmatrix}$$

$$R \sim LKJ(\eta)$$

Lewandowski-Kurowicka-Joe (LKJ) distribution with $\eta$ as **regularization hyperparameter

• if $\eta < 1$ prior with strong correlation unsure of postive or negative

• if $\eta = 1$ flat prior between - 1 and 1

• if $\eta > 1$ prior indicating low correlation

For $\tau$ we can use a Gamma prior (or here the exponential special case). It use two parameters : shape and scale.

Finaly for $\pi$ we know that the sum of them will be one (remember they are the relative proportion of the variability between group). This means we will be able to use a symmetric Dirichlet($2, \delta$). $\delta$ is called a concentration hyperparameter.

In this case with two group it can be define as a Beta distribution with both ($\delta$).

• if $\delta < 1$ more prior on $\pi_0$ on 0, 1 -> either a lot of few of the variability between group is explained with intercept

• $\delta = 1$ flat prior on $\pi_0$ variability of the intercept can explain from 0 to all the variability between groups

• $\delta > 1$ our prior is that around half of the variability between group is explained by differences in intercepts and rest with slopes.

To sum it up when we use rstanarm decov():

• reg = 1 is for $R \sim LKJ(1)$

• shape = 1 , scale = 1 is for $\tau \sim Gamma(1,1)$ or $Exp(1)$

• conc = 1 is for $Dirichlet(2,1)$ (two parameters with $\delta = 1$)

17.4.2 Posterior simulation and anlysis

running_model_2 <- stan_glmer(
  net ~ age + (age | runner),
  data = running, family = gaussian,
  prior_intercept = normal(100, 10),
  prior = normal(2.5, 1), 
  prior_aux = exponential(1, autoscale = TRUE),
  prior_covariance = decov(reg = 1, conc = 1, shape = 1, scale = 1),
  chains = 4, iter = 5000*2, seed = 84735, adapt_delta = 0.99999 # change here 
)

Now we have 78 parameters (36 for intercepts / 36 age coefficient and 6 global parameters) !

My poor laptop have done it in 33 minutes!

17.4.2.1 Global / Group specific parameters :

$$\beta_0 + \beta_1 X$$

# Quick summary of global regression parameters
tidy(running_model_2, effects = "fixed", conf.int = TRUE, conf.level = 0.80)
# A tibble: 2 x 5
  term        estimate std.error conf.low conf.high
  <chr>          <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)    18.5     11.6       3.61     33.6 
2 age             1.32     0.217     1.04      1.59

We need to move the MCMC simulations result into a friendlier objet:

# str(running_model_2) try it!

runner_chains_2 <- running_model_2 |>
  spread_draws(`(Intercept)`, b[term, runner], `age`) |> 
  pivot_wider(names_from = term, names_glue = "b_{term}",
              values_from = b) |> 
  mutate(runner_intercept = `(Intercept)` + `b_(Intercept)`,
         runner_age = age + b_age)
dim(runner_chains_2)

We need to summarize a bit:

runner_summaries_2 <- runner_chains_2 |> 
  group_by(runner) |> 
  summarize(runner_intercept = median(runner_intercept),
            runner_age = median(runner_age))

# Check it out
head(runner_summaries_2, 3)
saveRDS(runner_summaries_2, "data/ch17/runner_summaries_2")

runner_summaries_2 <- readRDS("data/ch17/runner_summaries_2")
ggplot(running, aes(y = net, x = age, group = runner)) + 
  geom_abline(data = runner_summaries_2, color = "gray",
              aes(intercept = runner_intercept, slope = runner_age)) + 
  lims(x = c(50, 61), y = c(50, 135))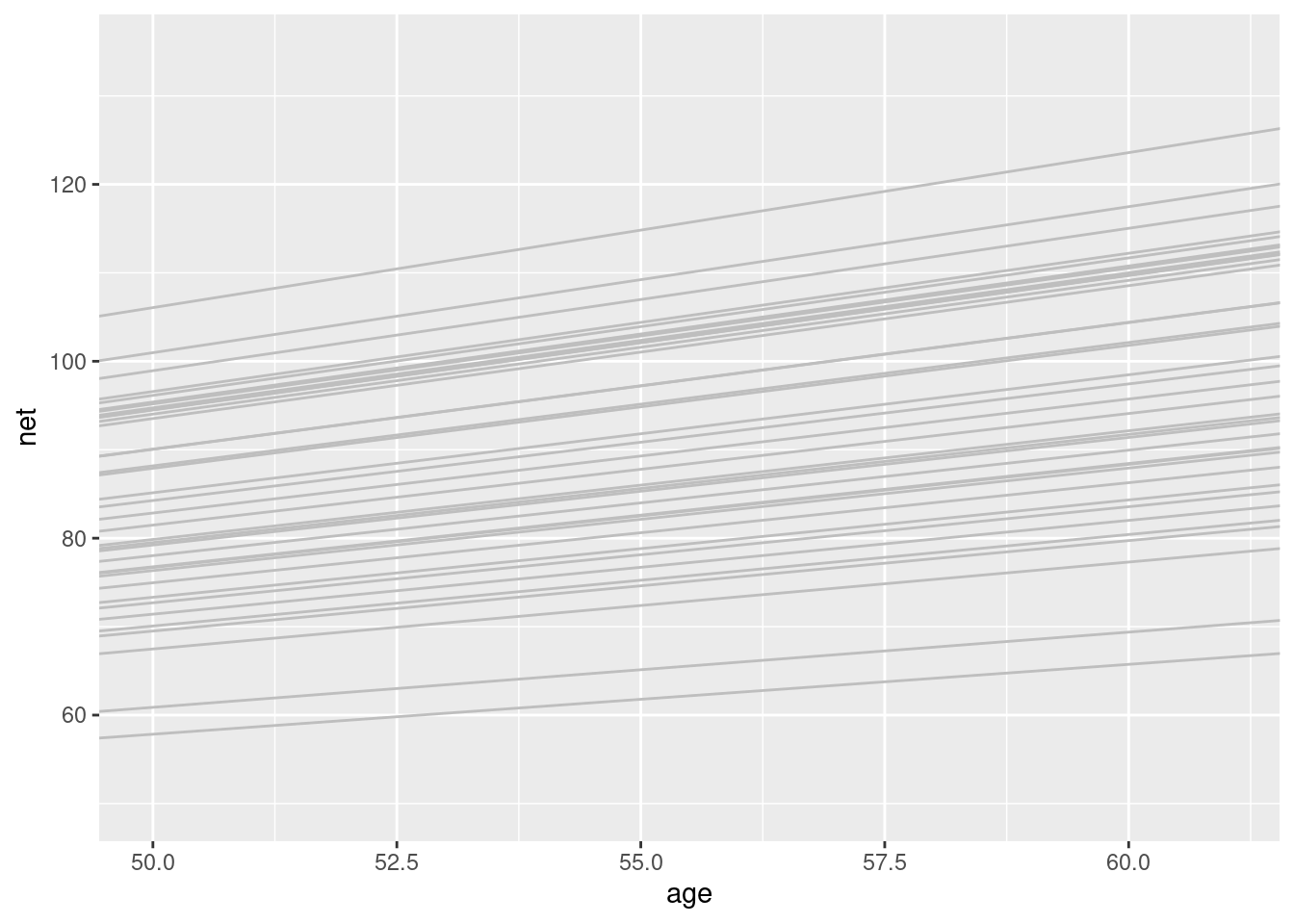

They slopes differ but no so much -> shrinkage the model is still trying to balance between a complete pooled models and a no pooled one (see fig 17.16).

17.4.2.2 Within- and between-group variability

is it worth it ?

tidy(running_model_2, effects = "ran_pars")
# A tibble: 4 x 3
  term                       group    estimate
  <chr>                      <chr>       <dbl>
1 sd_(Intercept).runner      runner     1.34  
2 sd_age.runner              runner     0.251 
3 cor_(Intercept).age.runner runner    -0.0955
4 sd_Observation.Residual    Residual   5.17  

We had 5.25 as $\sigma_y$ before, We have very slight correlation between $\beta_0j$ and $\beta_1j$.