16.3 No pooled model

ggplot(spotify, aes(x = popularity, group = artist)) + 
  geom_density()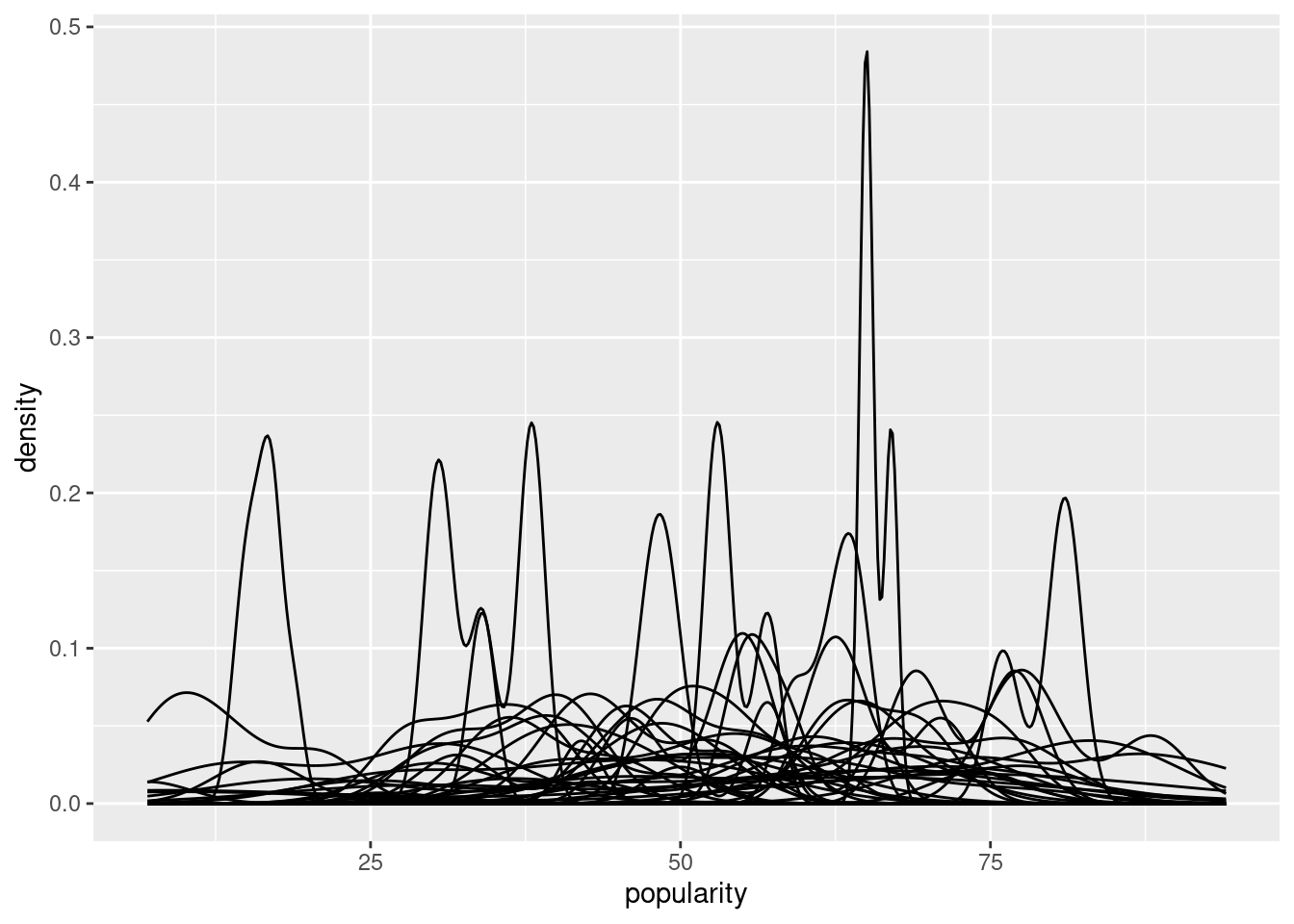

Key points:

  • popularity can differ from one artist to an other

  • some artist have a “stable” popularity across their song and some not

Let change our model to reflect that:

\[Y_{ij}|\mu_j, \sigma \sim N(\mu_{j}, \sigma^2 ) \] \(\mu_{j}\) : mean song popularity for artist \(j\)

\(\sigma\) : standard deviation in popularity from song to song within each artist

spotify_no_pooled <- stan_glm(
  popularity ~ artist - 1, 
  data = spotify, family = gaussian, 
  prior = normal(50, 2.5, autoscale = TRUE),
  prior_aux = exponential(1, autoscale = TRUE),
  chains = 4, iter = 5000*2, seed = 84735)

16.3.1 Same Quiz but with no pooling!!

3 artist:

  • Mia X, artist with the lowest mean popularity in our data set
  • Beyoncé, artist with nearly the highest mean popularity in our data set
  • Mohsen Beats, an artist not in out data set
set.seed(84735)
predictions_no <- posterior_predict(
  spotify_no_pooled, newdata = artist_means)
  
# Plot the posterior predictive intervals
ppc_intervals(artist_means$popularity, yrep = predictions_no, 
              prob_outer = 0.80) +
  ggplot2::scale_x_continuous(labels = artist_means$artist, 
                              breaks = 1:nrow(artist_means)) +
  xaxis_text(angle = 90, hjust = 1)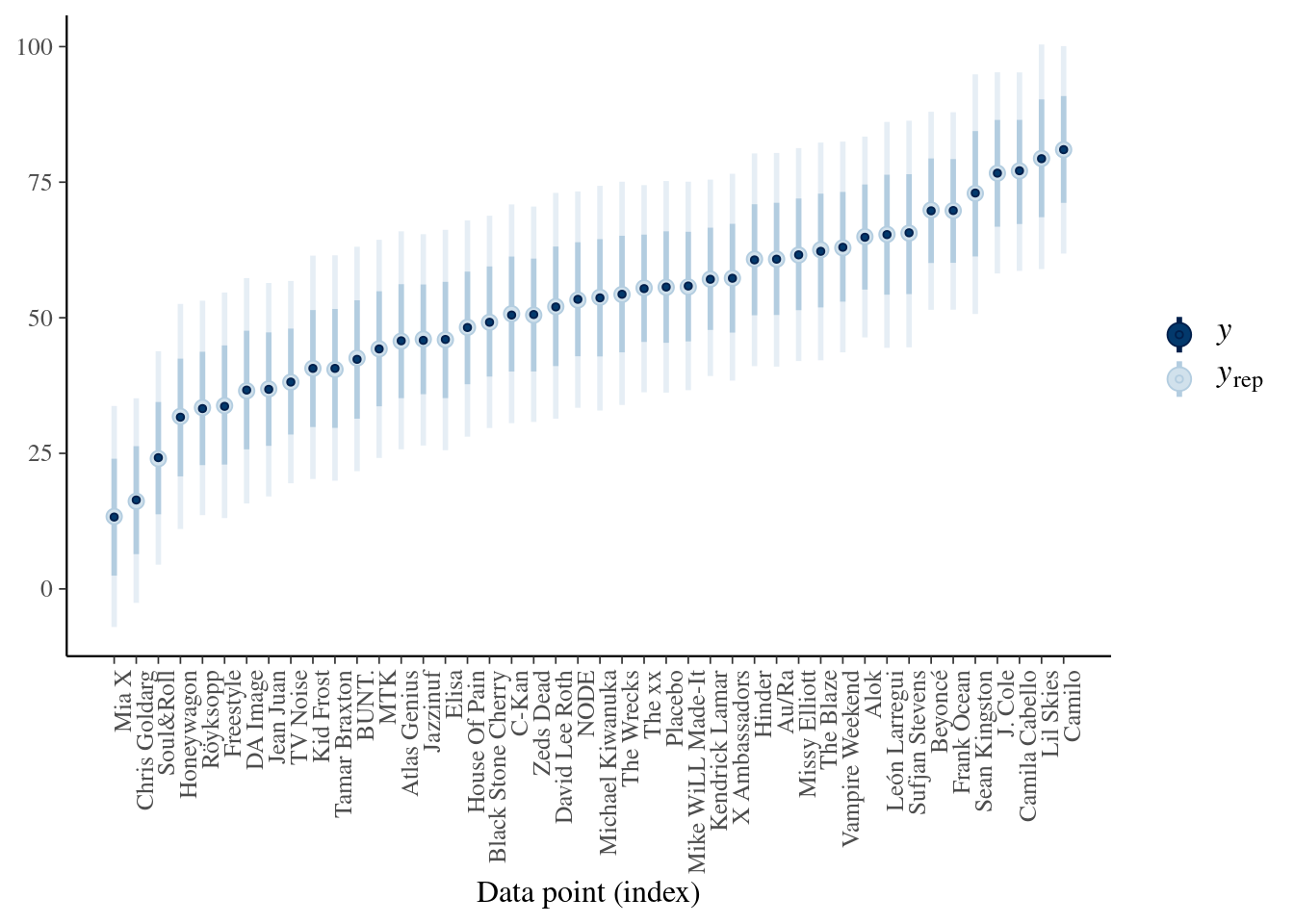

Two drawbacks:

  1. Ignoring other artist when modeling for one specific artist (what happens when fewer data point)

  2. If we assume no other artists help us understanding popularity of a specific artist we can not generalize to artist outside of our data set.