8.1 Introduction

What are the chances that this modern artist is Gen X or even younger, i.e., born in 1965 or later?

“modern” art doesn’t necessarily mean “new” art

Speculating assumptions:

major modern art museums disproportionately display artists born before 1965.

  • \(n=100\) artists

  • \(\pi\) is the proportion of artists represented in major U.S. modern art museums that are Gen X or younger, it most likely falls below 0.5.

  • \(Beta(4,6)\) is the prior model for \(\pi\)

library(bayesrules)
library(tidyverse)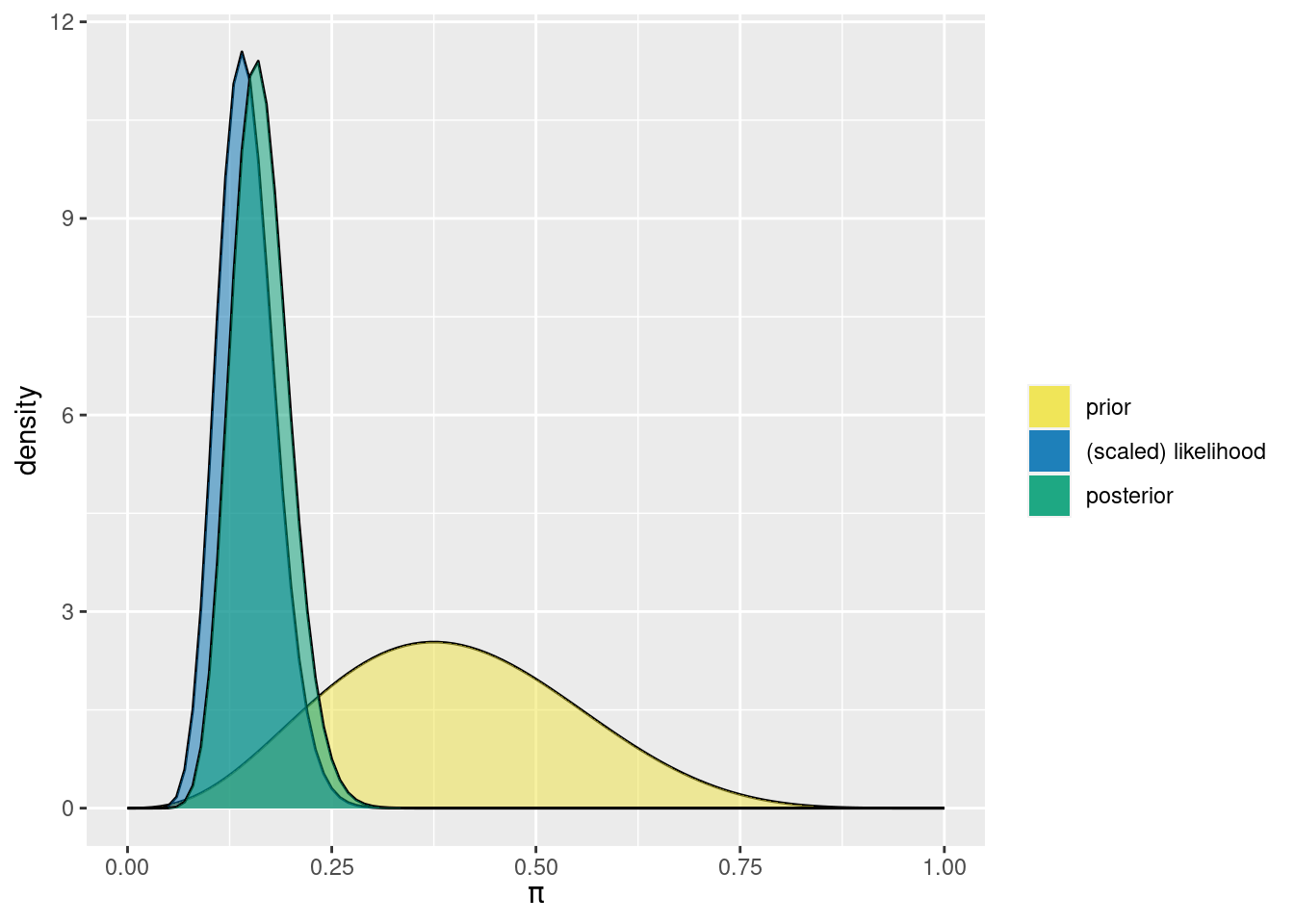

We use a dataset in the {bayesrules} package which contains data made available by MoMA.

data("moma_sample")
moma_sample%>%head
               artist  country birth death alive  genx gender count
1        Ad Gerritsen    dutch  1940  2015 FALSE FALSE   male     1
2 Kirstine Roepstorff   danish  1972  <NA>  TRUE  TRUE female     3
3    Lisa Baumgardner american  1958  2015 FALSE FALSE female     2
4         David Bates american  1952  <NA>  TRUE FALSE   male     1
5          Simon Levy american  1946  <NA>  TRUE FALSE   male     1
6      Pierre Mercure canadian  1927  1966 FALSE FALSE   male     8
  year_acquired_min year_acquired_max
1              1981              1981
2              2005              2005
3              2016              2016
4              2001              2001
5              2012              2012
6              2008              2008

genx are artists 14 or younger:

moma_sample %>%
  count(genx)%>%
  mutate(prop=n/sum(n))
##    genx  n prop
## 1 FALSE 86 0.86
## 2  TRUE 14 0.14

We use a Beta-Binomial framework as \(Y\) (genx) follows a Binomial model.

\[Y|\pi \sim Bin(100,\pi)\] \[\pi \sim Beta(4,6)\]

The posterior distribution is obtained:

\(\alpha=4\) set to this value \(\beta=6\)

\[\pi|(Y=y) \sim Beta(\alpha + \beta, \beta +n-y)\]

\[\pi|(Y=14) \sim Beta(18,92)\]

Tasks in posterior analysis:

  • estimation
  • hypothesis testing
  • prediction.