14.3 One Categorical Predictor
Suppose an Antarctic researcher comes across a penguin that weighs less than 4200g with a 195mm-long flipper and 50mm-long bill. Our goal is to help this researcher identify the species of this penguin: Adelie, Chinstrap, or Gentoo
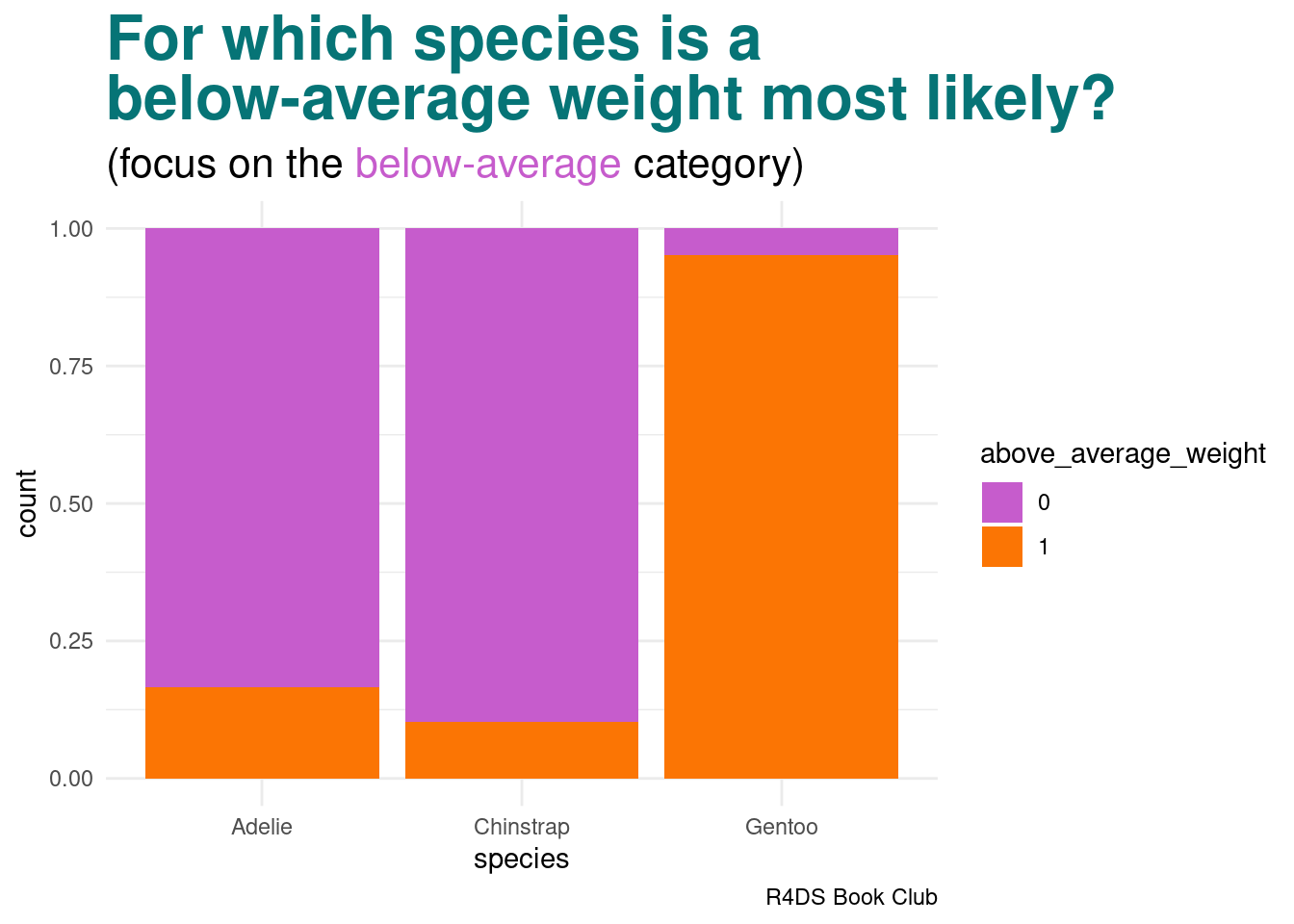
image code
penguins |>
drop_na(above_average_weight) |>
ggplot(aes(fill = above_average_weight, x = species)) +
geom_bar(position = "fill") +
labs(title = "<span style = 'color:#067476'>For which species is a<br>below-average weight most likely?</span>",
subtitle = "(focus on the <span style = 'color:#c65ccc'>below-average</span> category)",
caption = "R4DS Book Club") +
scale_fill_manual(values = c("#c65ccc", "#fb7504")) +
theme_minimal() +
theme(plot.title = element_markdown(face = "bold", size = 24),
plot.subtitle = element_markdown(size = 16))14.3.1 Recall: Bayes Rule
\[f(y|x_{1}) = \frac{\text{prior}\cdot\text{likelihood}}{\text{normalizing constant}} = \frac{f(y) \cdot L(y|x_{1})}{f(x_{1})}\] where, by the Law of Total Probability,
\[\begin{array}{rcl} f(x_{1} & = & \displaystyle\sum_{\text{all } y'} f(y')L(y'|x_{1}) \\ ~ & = & f(y' = A)L(y' = A|x_{1}) + f(y' = C)L(y' = C|x_{1}) + f(y' = G)L(y' = G|x_{1}) \\ \end{array}\]
over our three penguin species.
14.3.2 Calculation
penguins %>%
select(species, above_average_weight) %>%
na.omit() %>%
tabyl(species, above_average_weight) %>%
adorn_totals(c("row", "col"))## species 0 1 Total
## Adelie 126 25 151
## Chinstrap 61 7 68
## Gentoo 6 117 123
## Total 193 149 342Prior probabilities:
\[f(y = A) = \frac{151}{342}, \quad f(y = C) = \frac{68}{342}, \quad f(y = G) = \frac{123}{342}\]
Likelihoods:
\[\begin{array}{rcccl} L(y = A | x_{1} = 0) & = & \frac{126}{151} & \approx & 0.8344 \\ L(y = C | x_{1} = 0) & = & \frac{61}{68} & \approx & 0.8971 \\ L(y = G | x_{1} = 0) & = & \frac{6}{123} & \approx & 0.0488 \\ \end{array}\]
Total probability:
\[f(x_{1} = 0) = \frac{151}{342}\cdot\frac{126}{151} + \frac{68}{342}\cdot\frac{61}{68} + \frac{123}{342}\cdot\frac{6}{123} = \frac{193}{342}\]
Bayes’ Rules:
\[\begin{array}{rcccccl} f(y = A | x_{1} = 0) & = & \frac{f(y = A) \cdot L(y = A | x_{1} = 0)}{f(x_{1} = 0)} = \frac{\frac{151}{342}\cdot\frac{126}{151}}{\frac{193}{342}} & \approx & 0.6528 \\ f(y = C | x_{1} = 0) & = & \frac{f(y = A) \cdot L(y = C | x_{1} = 0)}{f(x_{1} = 0)} = \frac{\frac{68}{342}\cdot\frac{61}{68}}{\frac{193}{342}} & \approx & 0.3161 \\ f(y = G | x_{1} = 0) & = & \frac{f(y = A) \cdot L(y = G | x_{1} = 0)}{f(x_{1} = 0)} = \frac{\frac{123}{342}\cdot\frac{6}{123}}{\frac{193}{342}} & \approx & 0.0311 \\ \end{array}\]
The posterior probability that this penguin is an Adelie is more than double that of the other two species