3.8 Beta Posterior Model

We now have two pieces of our Bayesian model in place – the Beta prior model for Michelle’s support \(\pi\) and the Binomial model for the dependence of polling data Y on \(\pi\):

Y|\(\pi\) ~ Bin(50,\(\pi\))

\(\pi\) ~ Beta(45,55)

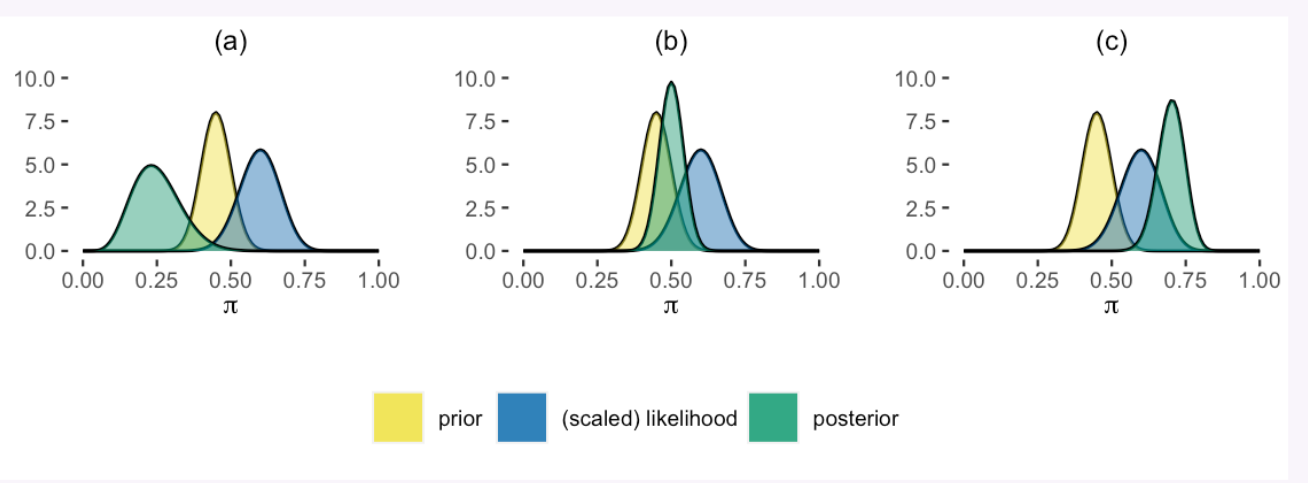
• The prior and data, as captured by the likelihood, don’t completely agree.

• Constructed from old polls, the prior is a bit more pessimistic about Michelle’s election support than the data obtained from the latest poll.

• Yet both insights are valuable to our analysis. Just as much as we shouldn’t ignore the new poll in favor of the old, we also shouldn’t throw out our bank of prior information in favor of the newest thing (also great life advice).

• Thinking like Bayesians, we can construct a posterior model of \(\pi\) which combines the information from the prior with that from the data.

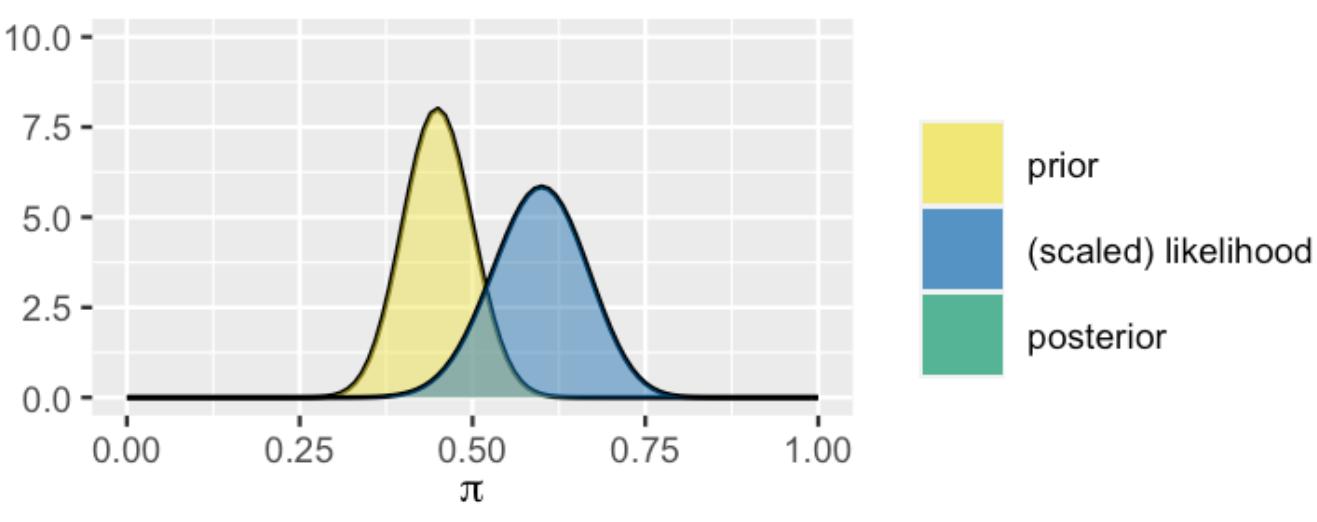The Posterior model of \(\pi\) along with the (scaled) likelihood function of \(\pi\) given the new poll results in which Y = 30 of n = 50 polled Minnesotans support Michelle.

What are we missing from this plot ?

Which plot reflects the correct posterior model of Michelle’s election support \(\pi\)?