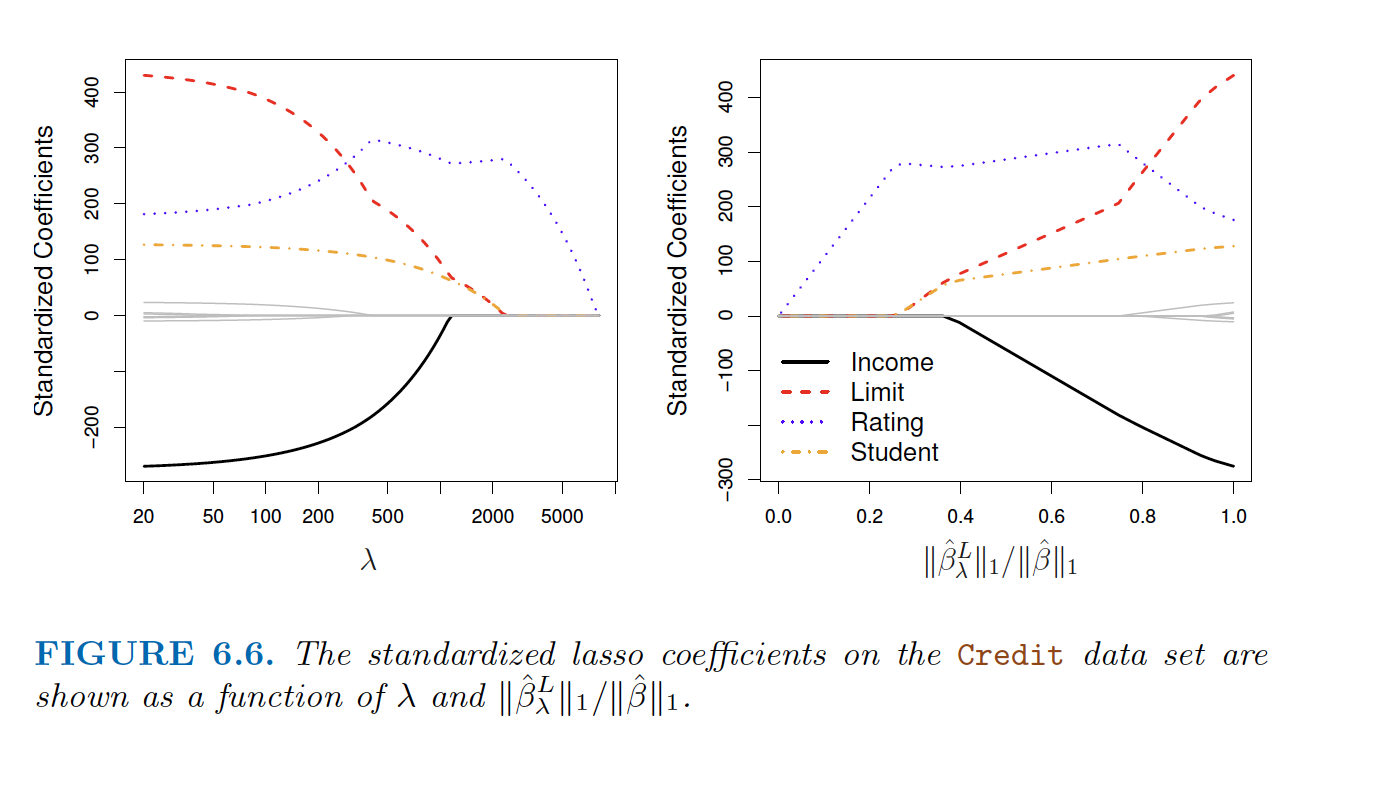
The Lasso

• $\hat{\beta}^L \equiv \underset{\hat{\beta}}{argmin}(RSS + \lambda\sum_{k=1}^p{|\beta_k|})$
• Shrinks some coefficients to 0 (creates sparse models)

The Lasso, Visually

Uses the 1-norm: $$\|\beta\|_1 = \sum_{j=1}^p{|\beta_j|}$$

How lasso eliminiates predictors.

It can be shown that these shrinkage methods are equivalent to a OLS with a constraint that depends on the type of shrinkage. For two parameters:

• $|\beta_1|+|\beta_2| \leq s$ for lasso,

• $\beta_1^2+\beta_2^2 \leq s$ for ridge,

The value of s depends on $\lambda$. (Larger s corresponds to smaller $\lambda$).

Graphically:

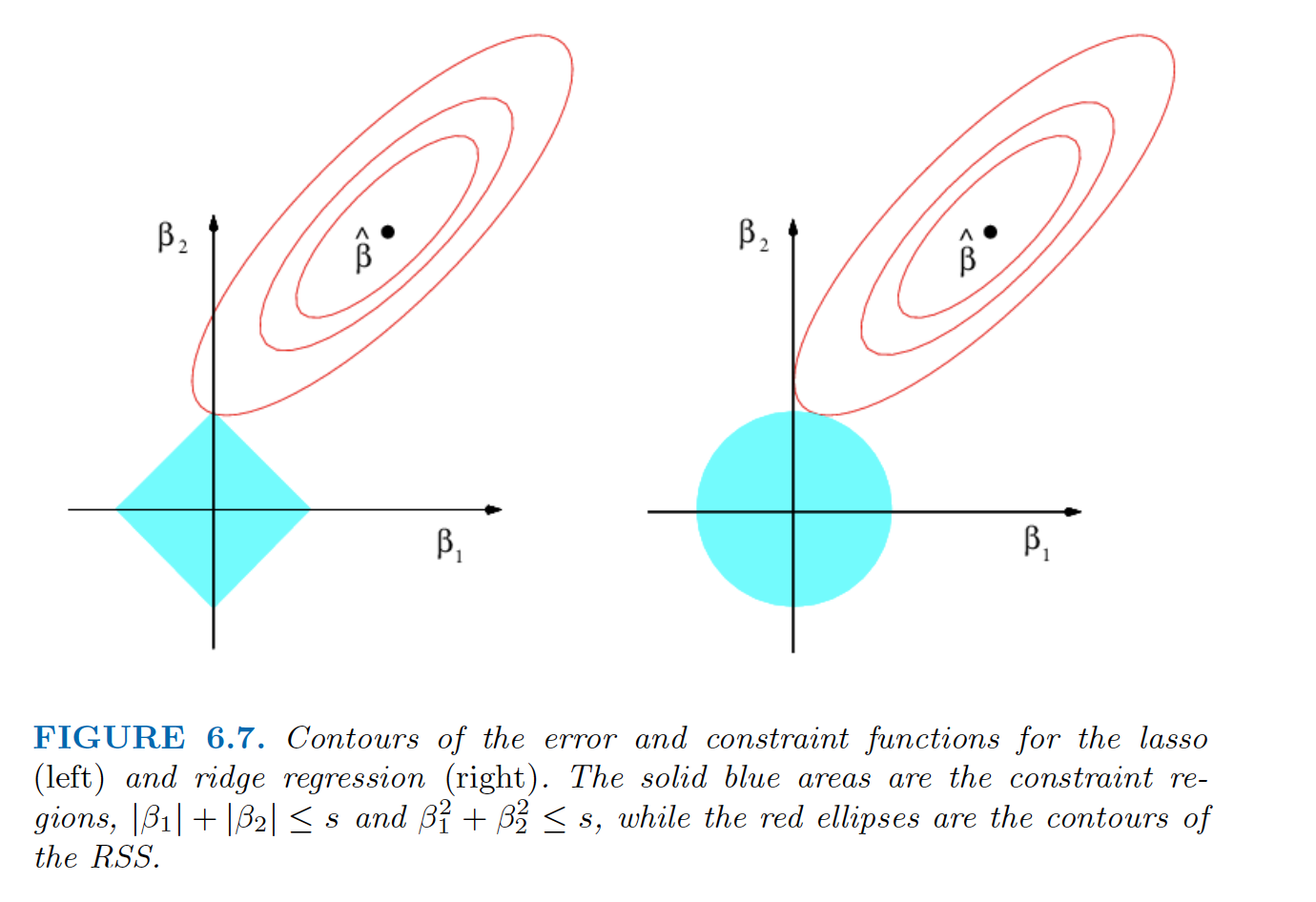
“the lasso constraint has corners at each of the axes, and so the ellipse will often intersect the constraint region at an axis”