4.8 Linear regression with count data - negative values

The results of fitting a least squares regression model to the Bikeshare data provides some reasonable results:

  • as weather progressively worsens, the number of bikers decreases (coefficients become negative wrt baseline)

  • the coefficients associated with season and time of day match expected patterns (lowest in winter, and highest during peak commute times)

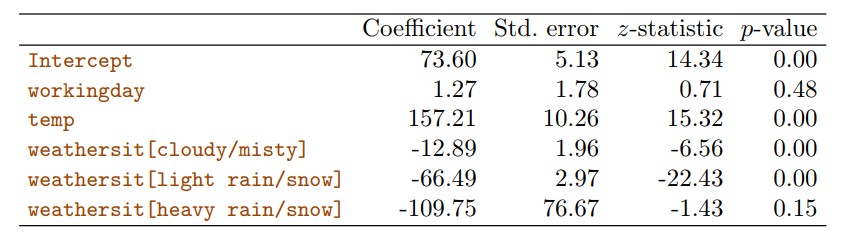
_Results for a least squares linear model fit to predict bikers in the Bikeshare data. For the qualitative variable weathersit, the baseline level corresponds to clear skies._

Figure 4.12: Results for a least squares linear model fit to predict bikers in the Bikeshare data. For the qualitative variable weathersit, the baseline level corresponds to clear skies.

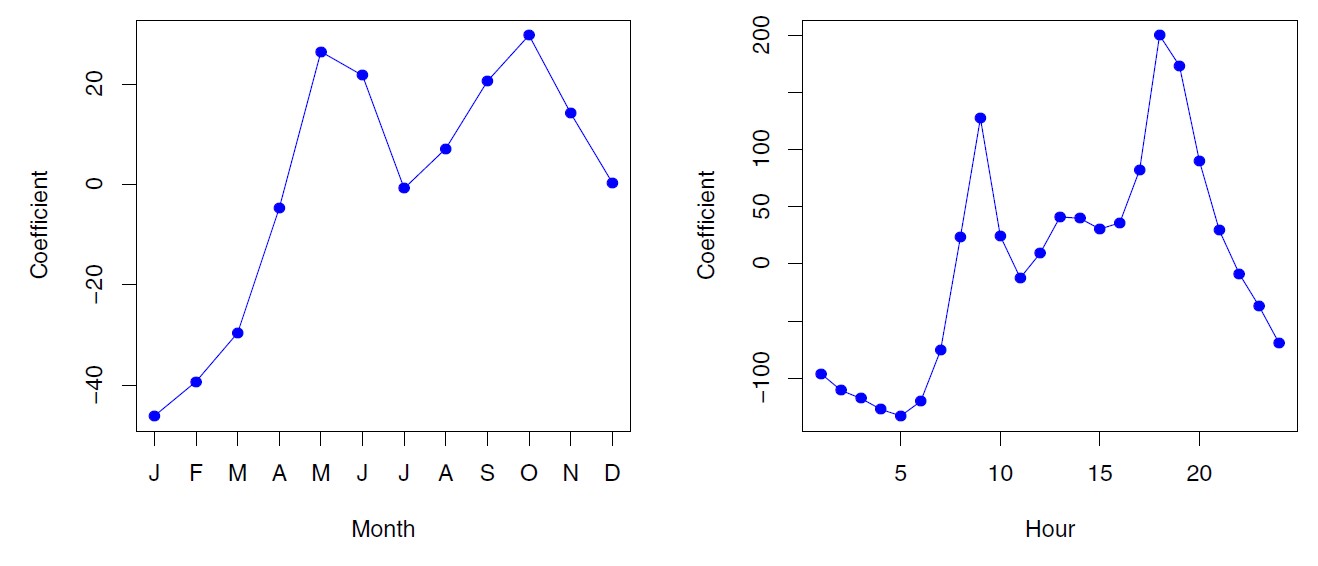
_A least squares linear regression model was fit to predict bikers in the Bikeshare data set. Left: The coefficients associated with the month of the year. Bike usage is highest in the spring and fall, and lowest in the winter. Right: The coefficients associated with the hour of the day. Bike usage is highest during peak commute times, and lowest overnight._

Figure 4.13: A least squares linear regression model was fit to predict bikers in the Bikeshare data set. Left: The coefficients associated with the month of the year. Bike usage is highest in the spring and fall, and lowest in the winter. Right: The coefficients associated with the hour of the day. Bike usage is highest during peak commute times, and lowest overnight.

Problem 1: model predicts negative numbers of bikers at times