Separating Hyperplane
- Consider a matrix X of dimensions \(n*p\), and a \(y_{i} \in \{-1, 1\}\). We have a new observation, \(x^*\), which is a vector \(x^* = (x^*_{1}...x^*_{p})^T\) which we wish to classify to one of two groups.
- We will use a separating hyperplane to classify the observation.
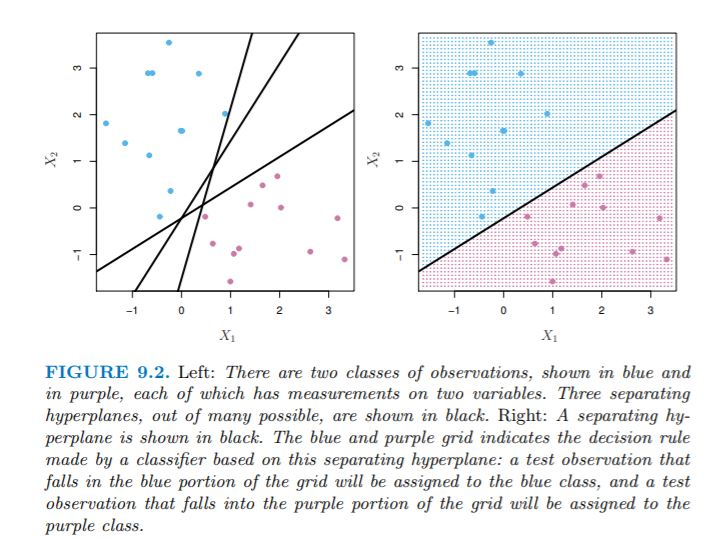
- We can label the blue observations as \(y_{i} = 1\) and the pink observations as \(y_{i} = -1\).
- Thus, a separating hyperplane has the property s.t. \(\beta_{0} + \beta_{1}X_{i1} + \beta_{2}X_{i2} ... + \beta_{p}X_{ip} > 0\) if \(y_{i} =1\) and \(\beta_{0} + \beta_{1}X_{i1} + \beta_{2}X_{i2} ... + \beta_{p}X_{ip} < 0\) if \(y_{i} = -1\).
- In other words, a separating hyperplane has the property s.t. \(y_{i}(\beta_{0} + \beta_{1}X_{i1} + \beta_{2}X_{i2} ... + \beta_{p}X_{ip}) > 0\) for all \(i = 1...n\).
- Consider also the magnitude of \(f(x^*)\). If it is far from zero, we are confident in its classification, whereas if it is close to 0, then \(x^*\) is located near the hyperplane, and we are less confident about its classification.
