4.6 Summary of the classification methods

4.6.1 An Analytical Comparison

  • LDA and logistic regression assume that the log odds of the posterior probabilities is linear in x.

  • QDA assumes that the log odds of the posterior probabilities is quadratic in x.

  • LDA is simply a restricted version of QDA with \(Σ_1 = · · · = Σ_K = Σ\)

  • LDA is a special case of naive Bayes and vice-versa!

  • LDA assumes that the features are normally distributed with a common within-class covariance matrix, and naive Bayes instead assumes independence of the features.

  • Naive Bayes can produce a more flexible fit.

  • QDA might be more accurate in settings where interactions among the predictors are important in discriminating between classes.

  • LDA > logistic regression when the observations at each Kth class is normal.

  • K-nearest neighbors (KNN) will be better classifiers when decision boudary is non-linear, n is large, and p is small.

  • KNN has low bias but large variance; as such, KNN requires a lot of observations relative to the number of predictors.

  • If decision boundary is non-linear but n is and p are small, then QDA may be preferred to KNN.

  • KNN does not tell us which predictors are important!


Final note. The choice of method depends on (1) the true distribution of the predictors in each of the K classes,(2) the values of n and p - bias-variance trade-off

4.6.2 An Empirical Comparison

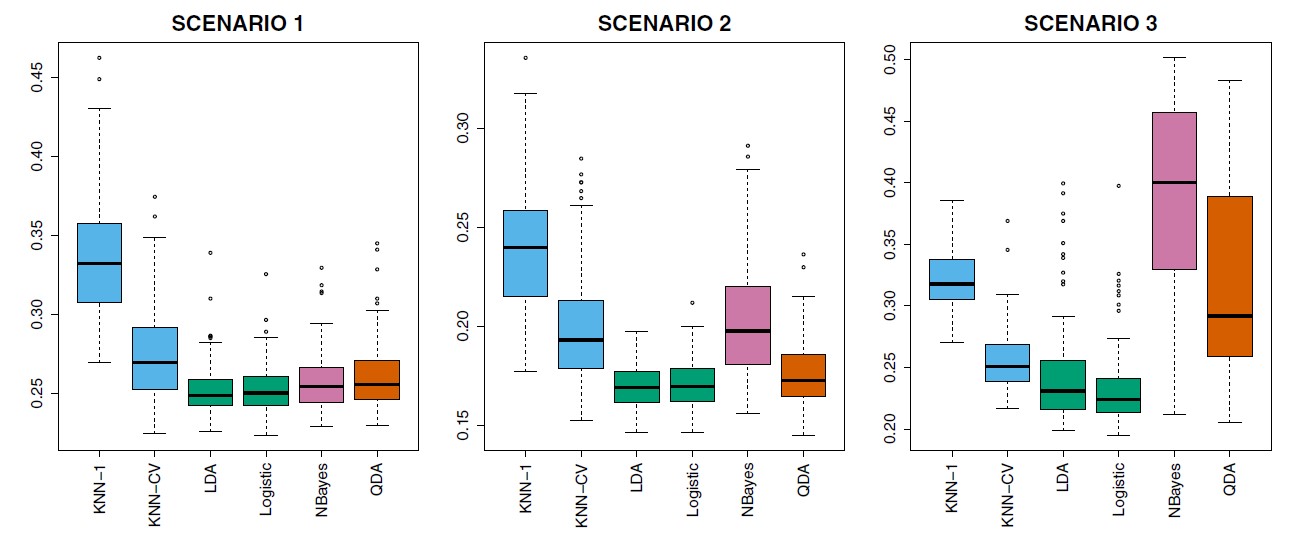
Boxplots of the test error rates for each of the linear scenarios described in the main text.

Figure 4.10: Boxplots of the test error rates for each of the linear scenarios described in the main text.

When Bayes decision boundary is linear,

Scenario 1: Binary class response, equal observations in each class, uncorrelated predictors

Scenario 2: Similar to Scenario 1, but the predictors had a correlation of −0.5.

Scenario 3: Predictors had a negative correlation, t-distribution (more extreme points at the tails)

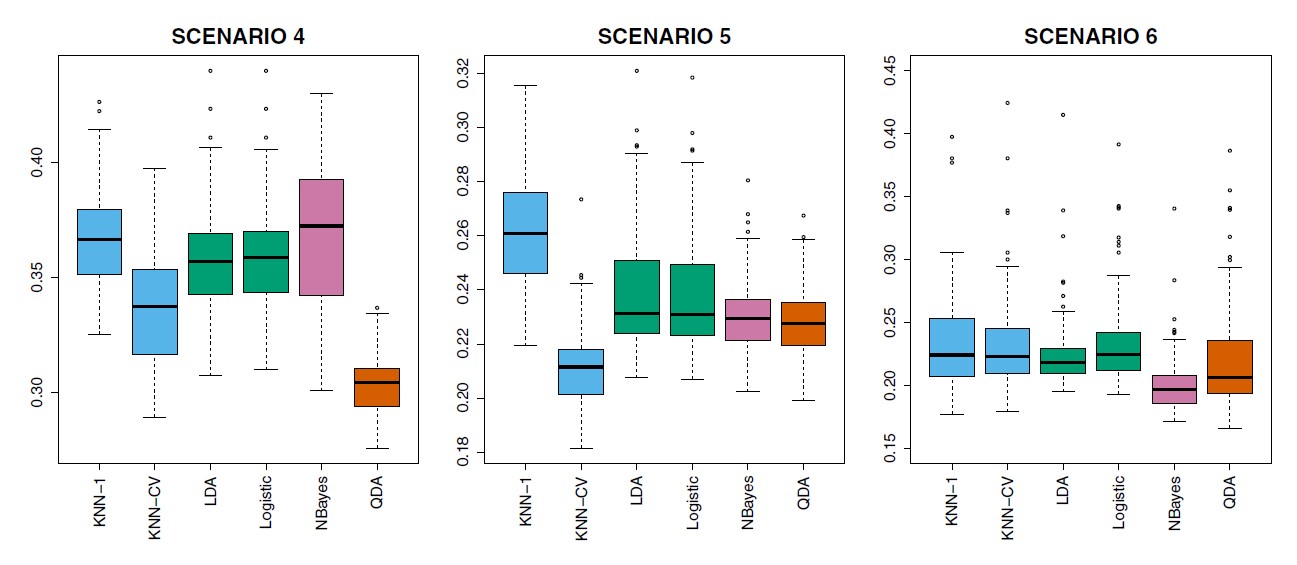
Boxplots of the test error rates for each of the non-linear scenarios described in the main text

Figure 4.11: Boxplots of the test error rates for each of the non-linear scenarios described in the main text

When Bayes decision boundary is non-linear,

Scenario 4: normal distiibution, correlation of 0.5 between the predictors in the first class, and correlation of −0.5 between the predictors in the second class.

Scenario 5: Normal distribution, uncorrelated predictors

Scenario 6: Normal distribution, different diagonal covariance matrix for each class, small n