Maximal Margin Classifier
- Generally, if data can be perfectly separated using a hyperplane, an infinite amount of such hyperplanes exist.
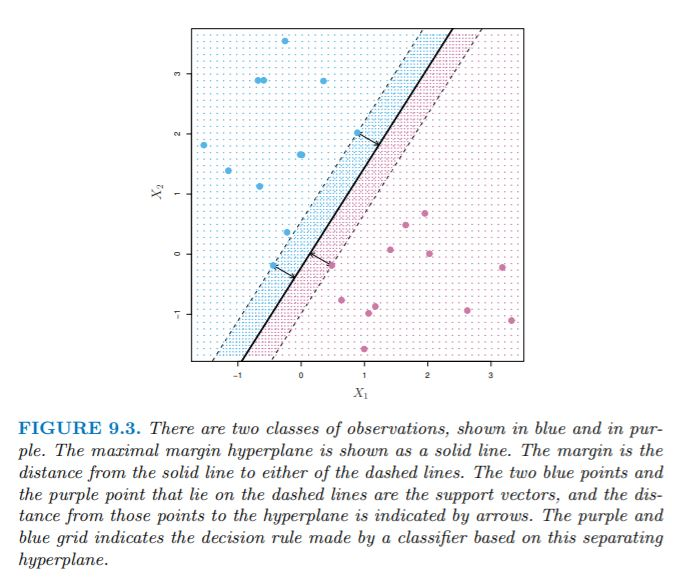
- An intuitive choice is the maximal margin hyperplane, which is the hyperplane that is farthest from the training data.
- We compute the perpendicular distance from each training observation to the hyperplane. The smallest of these distances is known as the margin.
- The maximal margin hyperplane is the hyperplane for which the margin is maximized. We can classify a test observation based on which side of the maximal margin hyperplane it lies on, and this is known as the maximal margin classifier.
- The maximal margin classifier classifies \(x^*\) based on the sign of \(f(x^*) = \beta_{0} + \beta_{1}x^*_{1} + ... + \beta_{p}x^*_{p}\).

- Note the 3 training observations that lie on the margin and are equidistant from the hyperplane. These are the support vectors (vectors in \(p\)-dimensional space; in this case \(p=2\)).
- They support the hyperplane because if their location was changed, the hyperplane would change.
- The maximal margin hyperplane depends on these observations, but not the others (unless the other observations were moved at or within the margin).

