4.3 Logistic Regression

4.3.1 The Logistic Model

  • Logistic regression: models the probability that Y belongs to a particular category (X)
  • X is binary (0/1)

\[p(X) = β_0 + β_1X \space \Longrightarrow {Linear \space regression}\] \[p (X) = \frac{e^{\beta_{0} + \beta_{1}X}}{1 + e^{\beta_{0} + \beta_{1}X}} \space \Longrightarrow {Logistic \space function}\] \[odds = \frac{p (X)}{1 - p (X)} = e^{\beta_{0} + \beta_{1}X} \Longrightarrow {odds \space value [0, ∞]}\]

By logging the whole equation, we get

\[\log \biggl(\frac{p(X)}{1- p(X)}\bigg) = \beta_{0} + \beta_{1}X \Longrightarrow {log \space odds/logit}\]

4.3.2 Estimating the Regression Coefficient

To estimate the regression coefficient, we use maximum likelihood (ME).

Likelihood Function

\[ℓ (\beta_{0}, \beta_{1}) = \prod_{i: y_{i}= 1} p (x_i) \prod_{i': y_{i'}= 0} (1- p (x_{i'})) \Longrightarrow {Likelihood \space function}\]

  • The aim is to find beta values such that \[ℓ\] is maximum.
  • The Least square method is the special case of maximum likelihood function.

4.3.3 Multiple Logistic Regression

\[\log \biggl(\frac{p(X)}{1- p(X)}\bigg) = \beta_{0} + \beta_{1}X_1 + ... + \beta_{p}X_p \\ \Downarrow \\ p(X) = \frac{e^{\beta_{0} + \beta_{1}X_1 + ... + \beta_{p}X_p}}{1 + \beta_{0} + \beta_{1}X_1 + ... + \beta_{p}X_p}\]

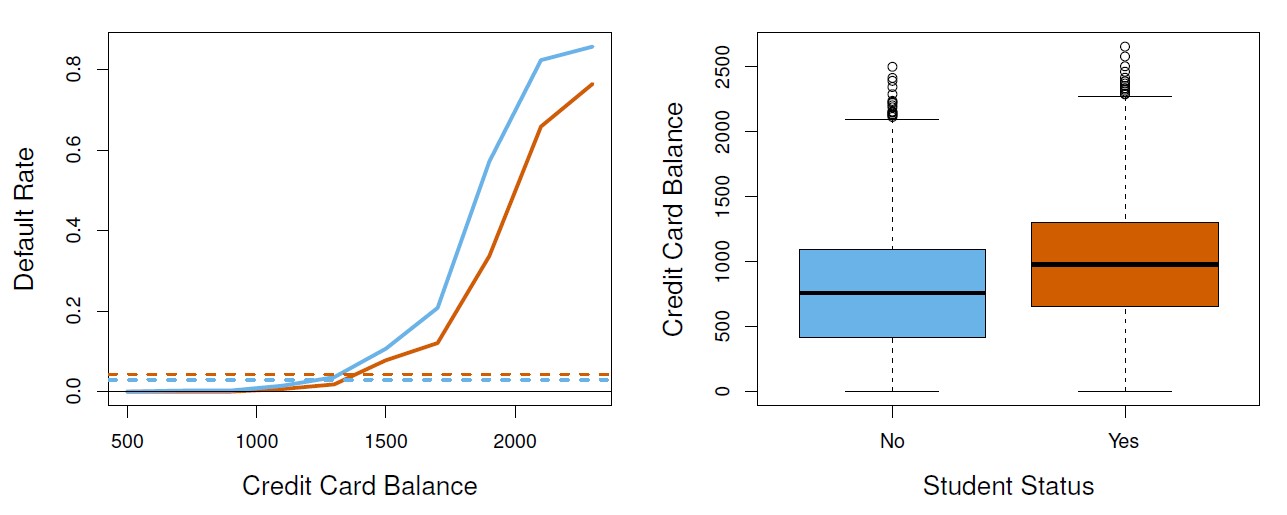
Confounding in the Default data. Left: Default rates are shown for students (orange) and non-students (blue). The solid lines display default rate as a function of balance, while the horizontal broken lines display the overall default rates. Right: Boxplots of balance for students (orange) and non-students (blue) are shown.

Figure 4.3: Confounding in the Default data. Left: Default rates are shown for students (orange) and non-students (blue). The solid lines display default rate as a function of balance, while the horizontal broken lines display the overall default rates. Right: Boxplots of balance for students (orange) and non-students (blue) are shown.

4.3.4 Multinomial Logistic Regression

  • This is used in the setting where K > 2 classes. In multinomial, we select a single class to serve as the baseline.

  • However, the interpretation of the coefficients in a multinomial logistic regression model must be done with care, since it is tied to the choice of baseline.

  • Alternatively, you can use `Softmax coding, where we treat all K classes symmetrically, and assume that for k = 1, . . . ,K, rather than selecting a baseline. This means, we estimate coefficients for all K classes, rather than estimating coefficients for K − 1 classes.