9.4 Mathematics of the MMC

• Consider constructing an MMC based on the training observations \(x_{1}...x_{n} \in \mathbb{R}^p\). This is the solution to the optimization problem:

\[\text{max}_{\beta_{0}...\beta_{p}, M} \space M\] \[\text{subject to } \sum_{j=1}^{p}\beta_{j}^2 = 1\] \[y_{i}(\beta_{0} + \beta_{1}X_{i1} + \beta_{2}X_{i2} ... + \beta_{p}X_{ip}) \geq M \quad \forall i = 1...n\]

• \(M\) is the margin, and the \(\beta\) coeffients are chosen to maximize \(M\).
• The constraint (3rd equation) ensures that each observation will be correctly classified, as long as M is positive.

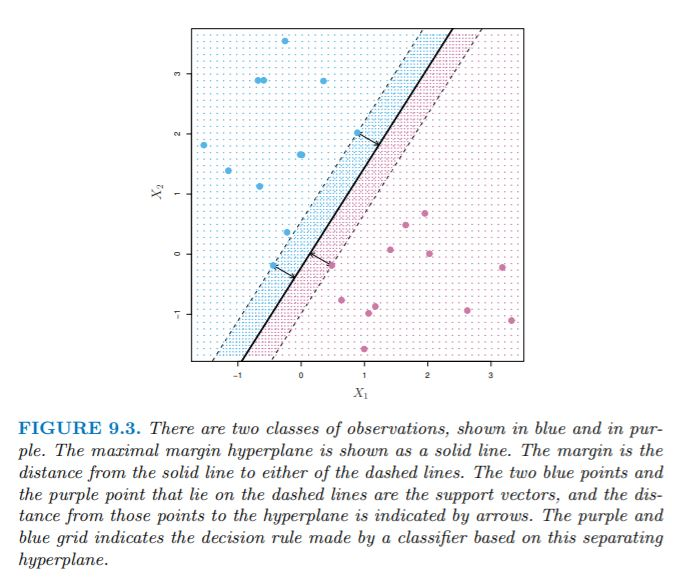
• The 2nd and 3rd equations ensure that each data point is on the correct side of the hyperplane and at least M-distance away from the hyperplane.
• The perpendicular distance to the hyperplane is given by \(y_{i}(\beta_{0} + \beta_{1}x_{i1} + \beta_{2}x_{i2} ... + \beta_{p}x_{ip})\).

But what if our data is not separable by a linear hyperplane?

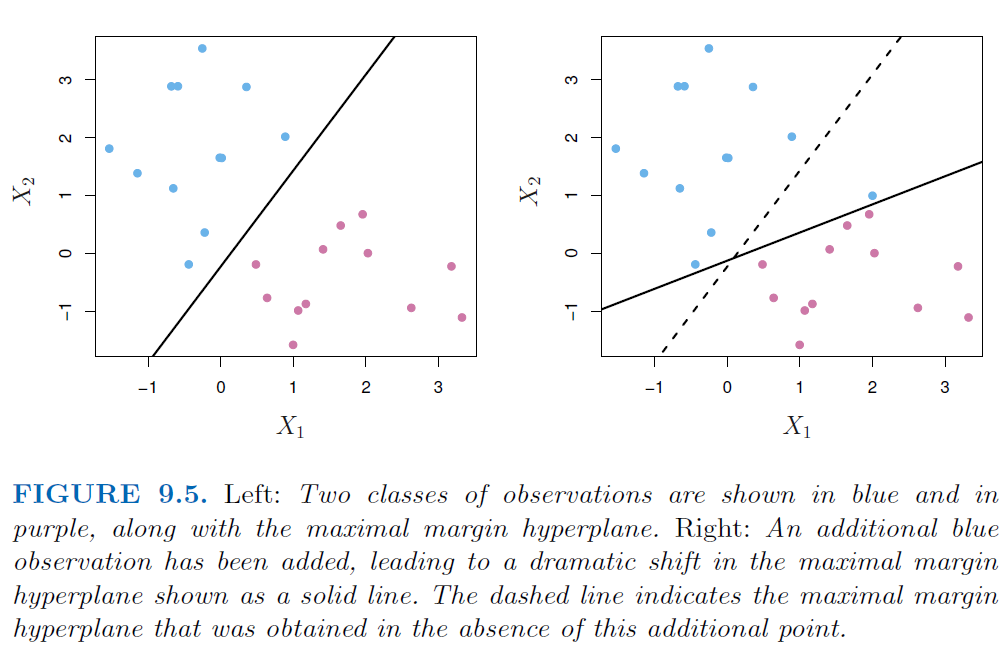
Individual data points greatly affect formation of the maximal margin classifier