6.4 Considerations in High Dimensions

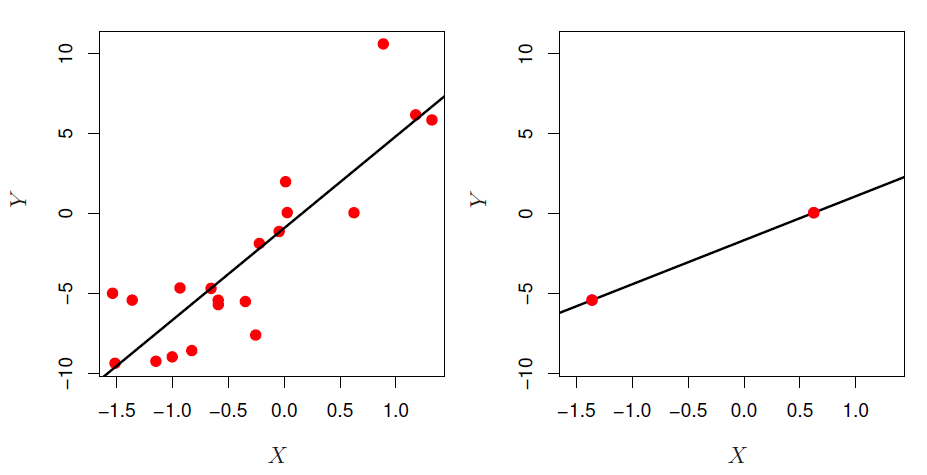
Figure 6.22

• Data sets containing more features $p$ than observations $n$ are often referred to as high-dimensional.
• Modern data can have a huge number of predictors (eg: 500k SNPs, every word ever entered in a search)
• When $n <= p$, linear regression memorizes the training data, but can suck on test data.

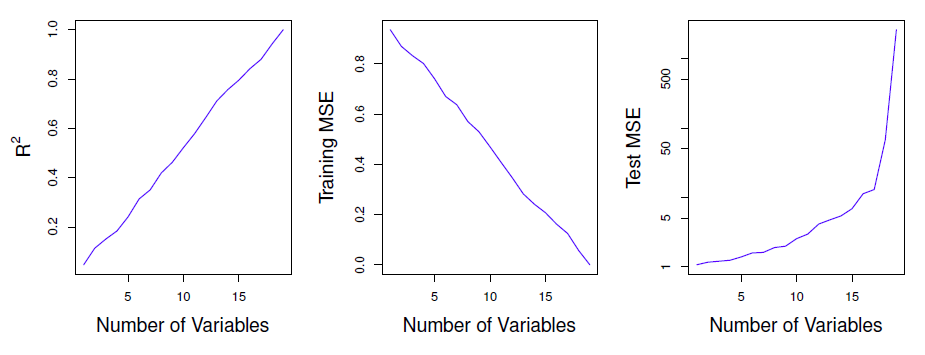
Figure 6.23 - simulated data set with n = 20 training observations, all unrelated to outcome.

Lasso (etc) vs Dimensionality

• Reducing flexibility (all the stuff in this chapter) can help.
• It’s important to choose good tuning parameters for whatever method you use.
• Features that aren’t associated with $Y$ increase test error (“curse of dimensionality”).
  • Fit to noise in training, noise in test is different.
• When $p > n$, never use train MSE, p-values, $R^2$, etc, as evidence of goodness of fit because they’re likely to be wildly different from test values.

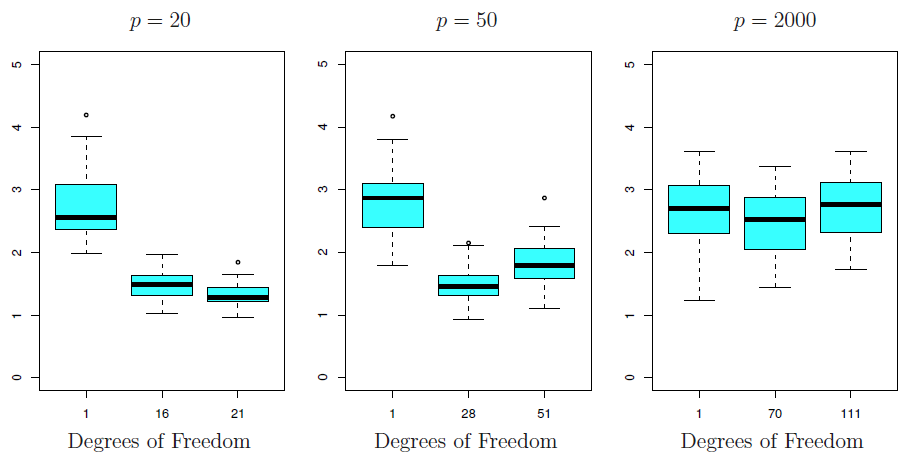
Figure 6.24