9.1 Hyperplane

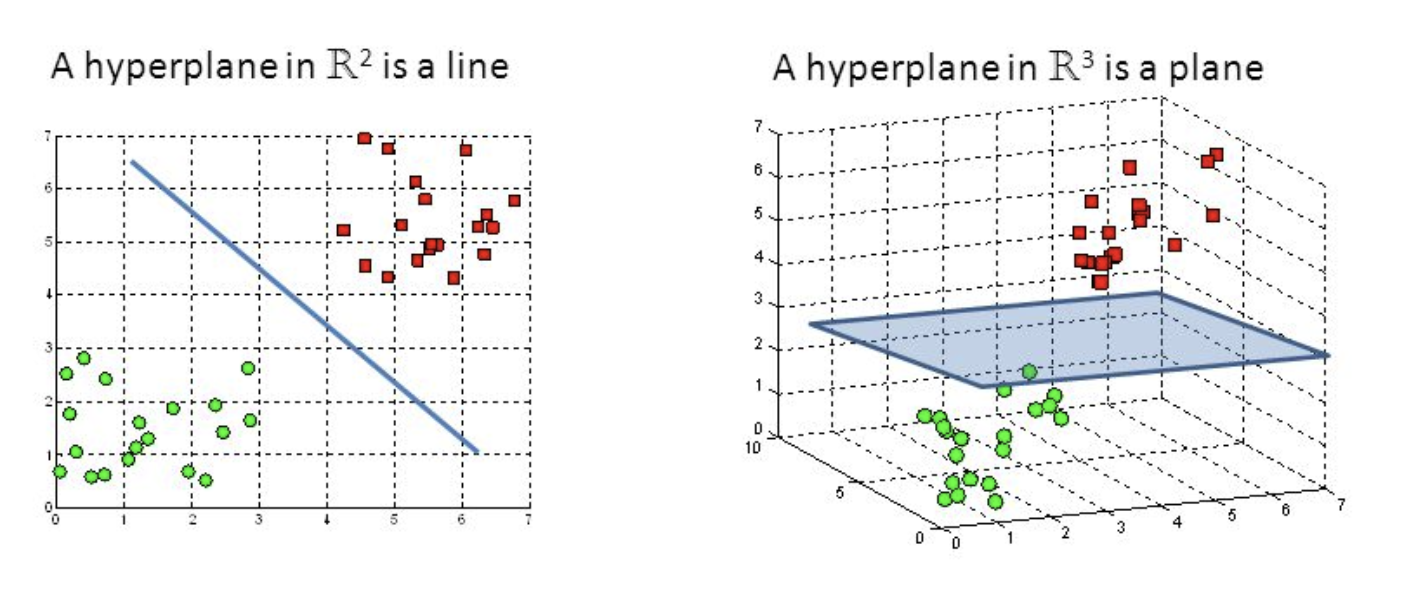
image credit: Deep AI

• A hyperplane is a $p-1$-dimensional flat subspace of a $p$-dimensional space. For example, in a 2-dimensional space, a hyperplane is a flat one-dimensional space: a line.
• (standard form) Definition of 2D hyperplane in 3D space: $$\beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \beta_{3}X_{3}= 0$$
• (inner products) Any $X$ s.t. $X = (X_{1}, X_{2})^T$ for which the equation above is satisfied is a point on the hyperplane.

Additional resource: Deep AI