Ridge Regression
Ridge regression is very similar to least squares, except that the coefcients are estimated by minimizing a slightly diferent quantity
\(\hat{\beta}^{OLS} \equiv \underset{\hat{\beta}}{argmin}(RSS)\)
\(\hat{\beta}^R \equiv \underset{\hat{\beta}}{argmin}(RSS+\lambda\sum_{k=1}^p{\beta_k^2})\)
\(\lambda\) tuning parameter (hyperparameter) for the shrinkage penalty
there’s one model parameter \(\lambda\) doesn’t shrink
- (\(\hat{\beta_0}\))
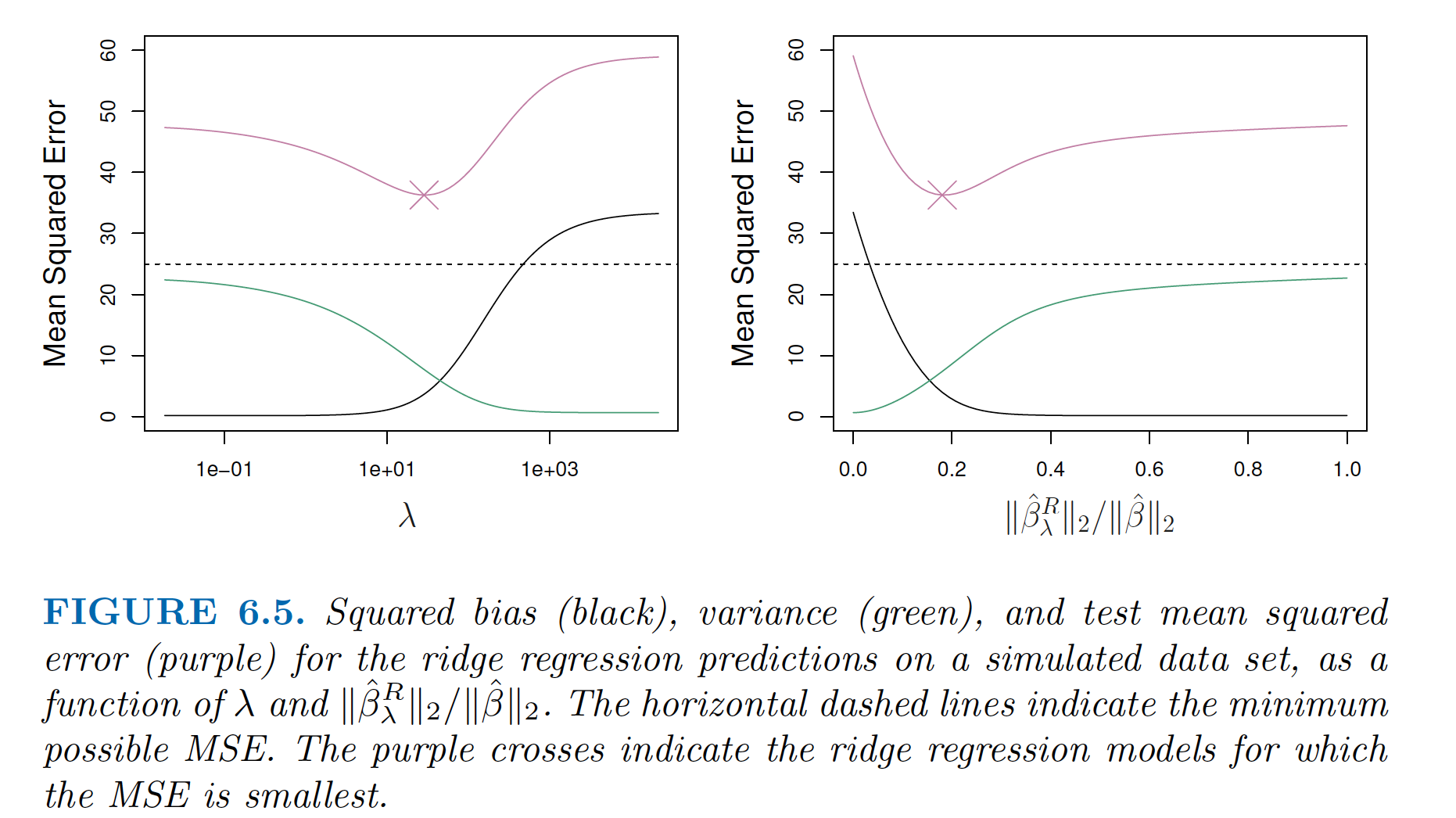
Ridge Regression, Visually
\[\|\beta\|_2 = \sqrt{\sum_{j=1}^p{\beta_j^2}}\]
Note the decrease in test MSE, and further that this is not computationally expensive: “One can show that computations required to solve (6.5), simultaneously for all values of \(\lambda\), are almost identical to those for fitting a model using least squares.”