9.3 Functions used to measure predictive strengths of a model

The assessment of the models is via empirical validation and grouped by the nature of the outcome data, and this can be done through:

  • Regression:

    • regression metrics (purely numeric)

  • Classification:

    • binary classes
    • multilevel metrics (three or more class levels)

9.3.1 Case Study 3

For this example data is from The Trust for Public Land for ranking the public parks in the US. The dataset ranges within a period between 2012 and 2020, in 102 US cities, parks are ranked by characteristics of services.

In particular we will be looking at selected amenities in the parks, which are things that conduce to comfort, convenience, or enjoyment.

https://github.com/rfordatascience/tidytuesday/blob/master/data/2021/2021-06-22/readme.md

  • Data load
library(tidytuesdayR)
tuesdata <- tidytuesdayR::tt_load(2021, week = 26)
## 
##  Downloading file 1 of 1: `parks.csv`
parks <- tuesdata$parks
parks%>%head
## # A tibble: 6 × 28
##    year  rank city    med_park_size_data med_park_size_points park_pct_city_data
##   <dbl> <dbl> <chr>                <dbl>                <dbl> <chr>             
## 1  2020     1 Minnea…                5.7                   26 15%               
## 2  2020     2 Washin…                1.4                    5 24%               
## 3  2020     3 St. Pa…                3.2                   14 15%               
## 4  2020     4 Arling…                2.4                   10 11%               
## 5  2020     5 Cincin…                4.4                   20 14%               
## 6  2020     6 Portla…                4.9                   22 18%               
## # ℹ 22 more variables: park_pct_city_points <dbl>, pct_near_park_data <chr>,
## #   pct_near_park_points <dbl>, spend_per_resident_data <chr>,
## #   spend_per_resident_points <dbl>, basketball_data <dbl>,
## #   basketball_points <dbl>, dogpark_data <dbl>, dogpark_points <dbl>,
## #   playground_data <dbl>, playground_points <dbl>, rec_sr_data <dbl>,
## #   rec_sr_points <dbl>, restroom_data <dbl>, restroom_points <dbl>,
## #   splashground_data <dbl>, splashground_points <dbl>, …
parks%>%names
##  [1] "year"                      "rank"                     
##  [3] "city"                      "med_park_size_data"       
##  [5] "med_park_size_points"      "park_pct_city_data"       
##  [7] "park_pct_city_points"      "pct_near_park_data"       
##  [9] "pct_near_park_points"      "spend_per_resident_data"  
## [11] "spend_per_resident_points" "basketball_data"          
## [13] "basketball_points"         "dogpark_data"             
## [15] "dogpark_points"            "playground_data"          
## [17] "playground_points"         "rec_sr_data"              
## [19] "rec_sr_points"             "restroom_data"            
## [21] "restroom_points"           "splashground_data"        
## [23] "splashground_points"       "amenities_points"         
## [25] "total_points"              "total_pct"                
## [27] "city_dup"                  "park_benches"
  • EDA: Exploratory data analysis
ggplot(parks,aes(x=year,y = rank))+
  geom_col(aes(fill=city)) +
  labs(x="Year", y = "Rank values")+
  guides(fill="none")+
  labs(title="US City Ranks per Year")+
  theme_minimal()

Select three years 2018, 2019, and 2020 and 99 cities, with full information.

parks_long <- parks %>%
  select(-amenities_points,-total_points,
         -contains("_data"),
         -park_benches,-city_dup)%>% 
  drop_na() %>%
  pivot_longer(
    cols = contains("_points"),
    names_to = "amenities",
    values_to = "points"
  ) %>%
  mutate(amenities=gsub("_points","",amenities))

parks_long%>% head
## # A tibble: 6 × 6
##    year  rank city        total_pct amenities          points
##   <dbl> <dbl> <chr>           <dbl> <chr>               <dbl>
## 1  2020     1 Minneapolis      85.3 med_park_size          26
## 2  2020     1 Minneapolis      85.3 park_pct_city          38
## 3  2020     1 Minneapolis      85.3 pct_near_park          98
## 4  2020     1 Minneapolis      85.3 spend_per_resident    100
## 5  2020     1 Minneapolis      85.3 basketball             47
## 6  2020     1 Minneapolis      85.3 dogpark                65
parks_long %>% 
  ggplot(aes(x = total_pct, y = rank, group=year,color=factor(year))) +
  geom_point(size = 0.5,
             alpha = 0.7) +
  geom_smooth(aes(color=factor(year)),linewidth=0.3,se=F) +
  scale_y_reverse()+
  scale_color_viridis(discrete = TRUE) +
  labs(title = "Amenities points",color="Year") +
  theme_minimal()

Let’s pose some questions before to choose:

  • What are we going to predict?

  • What is our research question?

  • Data Split

set.seed(123)
parks_split <- initial_split(parks_long, strata=rank,prop = 0.80)
parks_train <- training(parks_split)
parks_test  <- testing(parks_split)
  • Preprocessing steps: recipe() %>% step_*.*

This step involves setting the model formula and eventually make some data preprocessing with the help of the step_*.* functions.

In this case we don’t make any extra manipulations, in the first step of our model.

parks_rec <-
  recipe(
    rank ~ ., data = parks_train
  )
  • Set the Workflow

Wrap everything into a workflow.

# set model engine
lm_model <- linear_reg() %>% set_engine("lm") 

# use a workflow
lm_wflow <- 
  workflow() %>% 
  add_model(lm_model) %>% 
  add_recipe(parks_rec)

Fit the workflow with the training set.

lm_fit <- fit(lm_wflow, parks_train)

lm_fit %>% tidy() %>% head
## # A tibble: 6 × 5
##   term                    estimate std.error statistic   p.value
##   <chr>                      <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept)             -2162.     88.0       -24.6  3.71e-118
## 2 year                        1.14    0.0437     26.1  6.81e-131
## 3 cityAnaheim                 1.62    0.477       3.39 7.06e-  4
## 4 cityAnchorage              -1.08    0.438      -2.46 1.40e-  2
## 5 cityArlington, Texas        3.21    0.504       6.38 2.22e- 10
## 6 cityArlington, Virginia     9.39    0.621      15.1  2.53e- 49
  • Predict with new data from the testing set
# predict(lm_fit, parks_test %>% slice(1:3))
# test the model on new data
pred <- predict(lm_fit, 
                new_data = parks_test %>%
                  filter(city %in% c("Seattle","Atlanta","Baltimore")))
parks_test_res <- predict(lm_fit, 
                          new_data = parks_test %>% select(-rank)) %>% 
  bind_cols(parks_test %>% select(rank))
parks_test_res%>%head
## # A tibble: 6 × 2
##    .pred  rank
##    <dbl> <dbl>
## 1 0.0862     1
## 2 0.180      1
## 3 0.187      1
## 4 2.66       2
## 5 3.76       3
## 6 3.90       3
ggplot(parks_test_res, aes(x = rank, y = .pred)) + 
  # Create a diagonal line:
  geom_abline(lty = 2) + 
  geom_point(alpha = 0.5) + 
  labs(y = "Predicted Rank", x = "Rank") +
  # Scale and size the x- and y-axis uniformly:
  coord_obs_pred()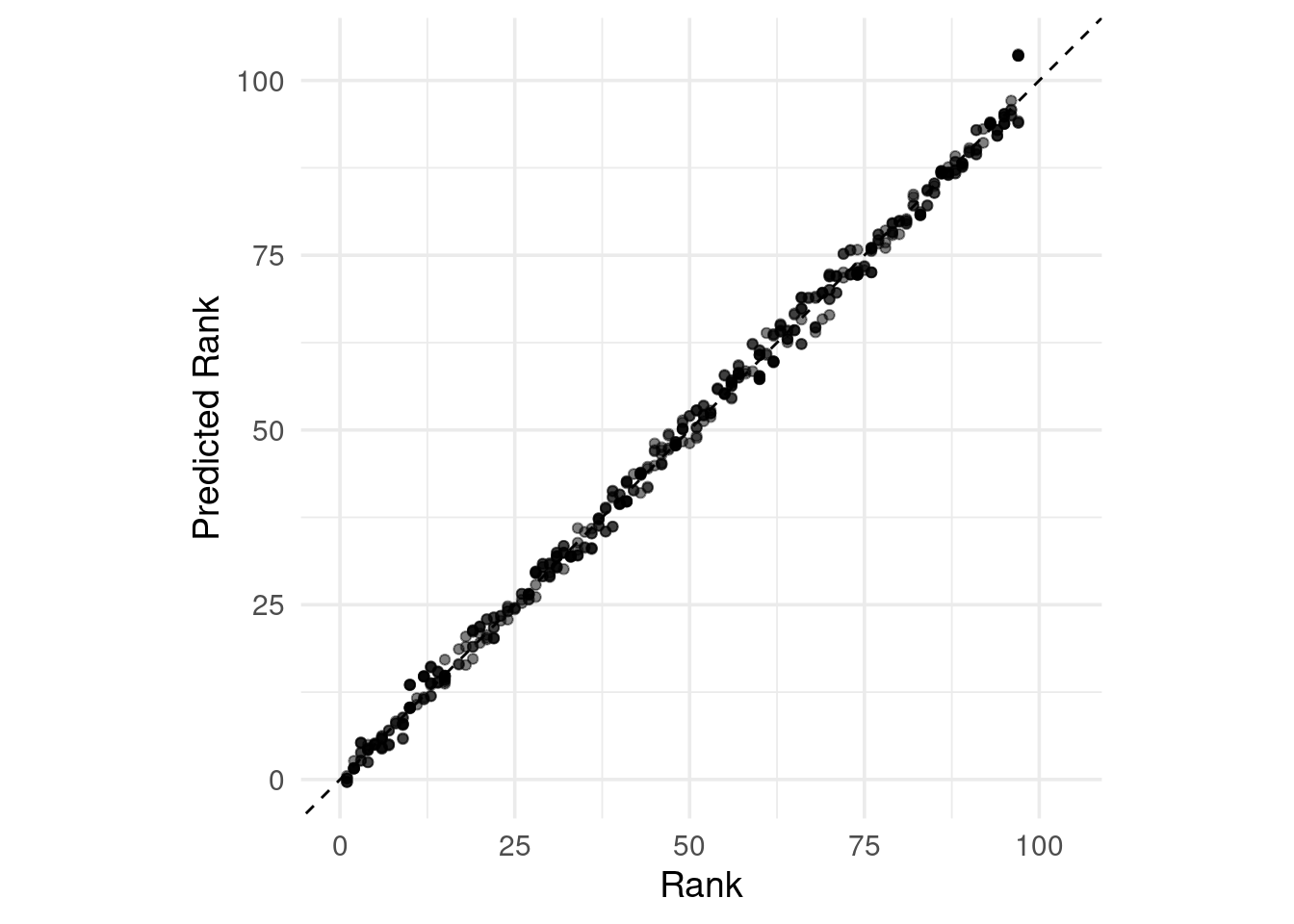

lm_fit%>%
  augment(new_data = parks_test %>% 
            filter(city %in% c("Seattle","Atlanta","Baltimore")))%>%
  group_by(city)%>%
  reframe(rank=mean(rank),.pred=mean(.pred))
## # A tibble: 3 × 3
##   city       rank .pred
##   <chr>     <dbl> <dbl>
## 1 Atlanta    41.2  41.9
## 2 Baltimore  60    60.0
## 3 Seattle    11    10.7
ggplot() +
  geom_point(data=parks_long,
         aes(x = total_pct, y = (rank)),
         color="grey0",
         size = 0.5,
         alpha = 0.7)+
  scale_y_reverse()+
  geom_smooth(data= lm_fit%>%
               augment(new_data = parks_test),
             aes(total_pct,.pred),
             color="darkred",
             size = 0.5,
             alpha = 0.7)

  • Apply the root mean squared error rmse()

The first measure used for the model is the root mean squared error: RMSE

# rmse(data, truth = outcome, estimate = .pred)
rmse(parks_test_res, truth = rank, estimate = .pred)
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard        1.57

Then make a comparison adding more metrics at once: Multiple metrics at once

# data_metrics <- metric_set(rmse, rsq, mae)
# data_metrics(data_test_res, truth = outcome, estimate = .pred)
parks_metrics <- metric_set(rmse, rsq, mae)
parks_metrics(parks_test_res, truth = rank, estimate = .pred)
## # A tibble: 3 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       1.57 
## 2 rsq     standard       0.997
## 3 mae     standard       1.21

Here we use some examples from the book with a sample predictions and multiple resampling:

Binary classes

  1. Confusion matrix:

Confusion matrix gives a holistic view of the performance of your model

What is a Confusion Matrix?

It is a matrix that contains values such as:

  • True Positive (TP)
  • True Negative (TN)
  • False Positive – Type 1 Error (FP)
  • False Negative – Type 2 Error (FN)

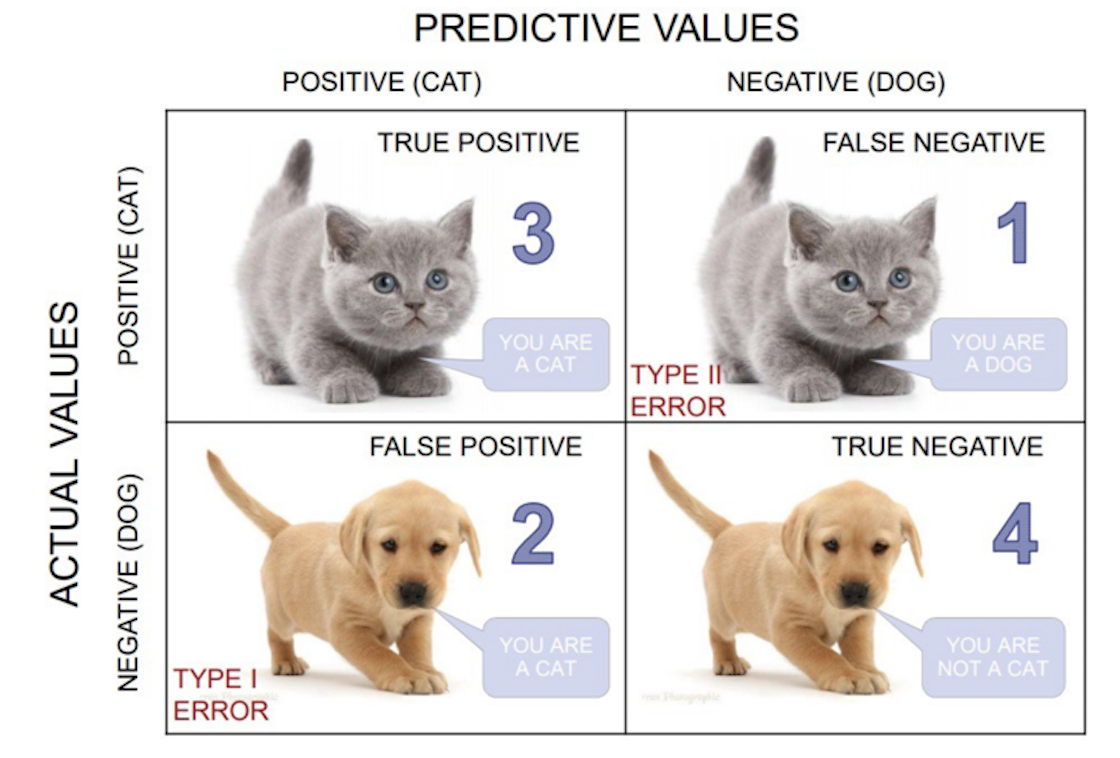
Confusion matrix

Example 1: two_class_example

data("two_class_example")
conf_mat(two_class_example, truth = truth, estimate = predicted)
##           Truth
## Prediction Class1 Class2
##     Class1    227     50
##     Class2     31    192

The confusion matrix contains other metrics that can be extracted under specific conditions.

  • Precision is how certain you are of your true positives
  • Recall is how certain you are that you are not missing any positives.

The measure used to estimate the effectiveness is the overall accuracy. It uses the hard class predictions to measure performance, which tells us whether our model is actually estimating a probability of cutoff to establish if the model predicted well or not with accuracy.

  1. Accuracy:
accuracy(two_class_example, truth = truth, estimate = predicted)
## # A tibble: 1 × 3
##   .metric  .estimator .estimate
##   <chr>    <chr>          <dbl>
## 1 accuracy binary         0.838
  1. Matthews correlation coefficient:
mcc(two_class_example, truth, predicted)
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 mcc     binary         0.677
  1. F1 metric: F1-score is a harmonic mean of Precision and Recall. The F1-score captures both the trends in a single value: when we try to increase the precision of our model, the recall (aka, sensitivity) goes down, and vice-versa.
f_meas(two_class_example, truth, predicted) #,event_level = "second")
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 f_meas  binary         0.849

All of the above have the event_level argument (first/second level)

To visualize the model metrics behavior, the receiver operating characteristic (ROC) curve computes the sensitivity and specificity over a continuum of different event thresholds

  • roc_curve() (curve)
  • roc_auc() (area)
two_class_curve <- roc_curve(two_class_example, truth, Class1)
  
two_class_curve %>% head
## # A tibble: 6 × 3
##   .threshold specificity sensitivity
##        <dbl>       <dbl>       <dbl>
## 1 -Inf           0                 1
## 2    1.79e-7     0                 1
## 3    4.50e-6     0.00413           1
## 4    5.81e-6     0.00826           1
## 5    5.92e-6     0.0124            1
## 6    1.22e-5     0.0165            1
roc_auc(two_class_example, truth, Class1)
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.939
autoplot(two_class_curve)

Multi-class

Finally we see data with three or more classes

  • Accuracy:
data(hpc_cv)
hpc_cv%>%head
##   obs pred        VF          F           M            L Resample
## 1  VF   VF 0.9136340 0.07786694 0.008479147 1.991225e-05   Fold01
## 2  VF   VF 0.9380672 0.05710623 0.004816447 1.011557e-05   Fold01
## 3  VF   VF 0.9473710 0.04946767 0.003156287 4.999849e-06   Fold01
## 4  VF   VF 0.9289077 0.06528949 0.005787179 1.564496e-05   Fold01
## 5  VF   VF 0.9418764 0.05430830 0.003808013 7.294581e-06   Fold01
## 6  VF   VF 0.9510978 0.04618223 0.002716177 3.841455e-06   Fold01
hpc_cv%>%
accuracy(obs, pred)
## # A tibble: 1 × 3
##   .metric  .estimator .estimate
##   <chr>    <chr>          <dbl>
## 1 accuracy multiclass     0.709
  • Matthews correlation coefficient:
mcc(hpc_cv, obs, pred)
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 mcc     multiclass     0.515

And then the sensitivity calculation for different estimators:

macro_sens <-sensitivity(hpc_cv, obs, pred, estimator = "macro");
weigh_sens <- sensitivity(hpc_cv, obs, pred, estimator = "macro_weighted");
micro_sens <- sensitivity(hpc_cv, obs, pred, estimator = "micro");
sens <- rbind(macro_sens,weigh_sens,micro_sens)
sens
## # A tibble: 3 × 3
##   .metric     .estimator     .estimate
##   <chr>       <chr>              <dbl>
## 1 sensitivity macro              0.560
## 2 sensitivity macro_weighted     0.709
## 3 sensitivity micro              0.709

And the ROC curve:

roc_auc(hpc_cv, obs, VF, F, M, L)
## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc hand_till      0.829

The ROC area:

roc_auc(hpc_cv, obs, VF, F, M, L, estimator = "macro_weighted")
## # A tibble: 1 × 3
##   .metric .estimator     .estimate
##   <chr>   <chr>              <dbl>
## 1 roc_auc macro_weighted     0.868

The ROC visualization: https://www.tidymodels.org/start/resampling/

hpc_cv %>% 
  group_by(Resample) %>%
  roc_curve(obs, VF, F, M, L) %>% 
  autoplot()

9.3.2 Conclusion

Judging the effectiveness of a variety of different models and to choose between them, we need to consider how well these models behave through the use of some performance statistics:

  • the area under the Receiver Operating Characteristic (ROC) curve, and
  • overall classification accuracy.

In conclusion when judging on a model effectiveness is important to follow few clear steps:

  • check of the data used for the modeling if contains any of the hidden information, such as modification of the units
  • second step is to calculate the ROC curve and the Area underneath the curve, plot it to see how it behaves on the model
  • third is to apply some selected metrics such as RMSE or RSQ, MAE etc.. to evaluate the estimation values
  • fourth make the confusion matrix as well as all the related metrics (sensitivity, specificity, accuracy, F1 …)
  • finally apply again the ROC curve visualization on resampling to see the best fit