19.6 Sparse autoencoders

They are used to extract the most influential feature representations, which helps to:

• Understand what are the most unique features of a data set
• Highlight the unique signals across the features.

19.6.1 Mathematical description

In the context of tanh activation function, we consider a neuron active if the output value is closer to 1 and inactive if its output is closer to -1, but we can increase the number of inactive neurons by incorporating sparsity (average activation of the coding layer).

$$\hat{\rho} = \frac{1}{m} \sum_{i=1}^m A(X)$$

Let’s get it from our example:

ae100_codings <- h2o.deepfeatures(best_model, features, layer = 1)
ae100_codings %>% 
    as.data.frame() %>% 
    tidyr::gather() %>%
    summarize(average_activation = mean(value))
##   average_activation
## 1        -0.00677801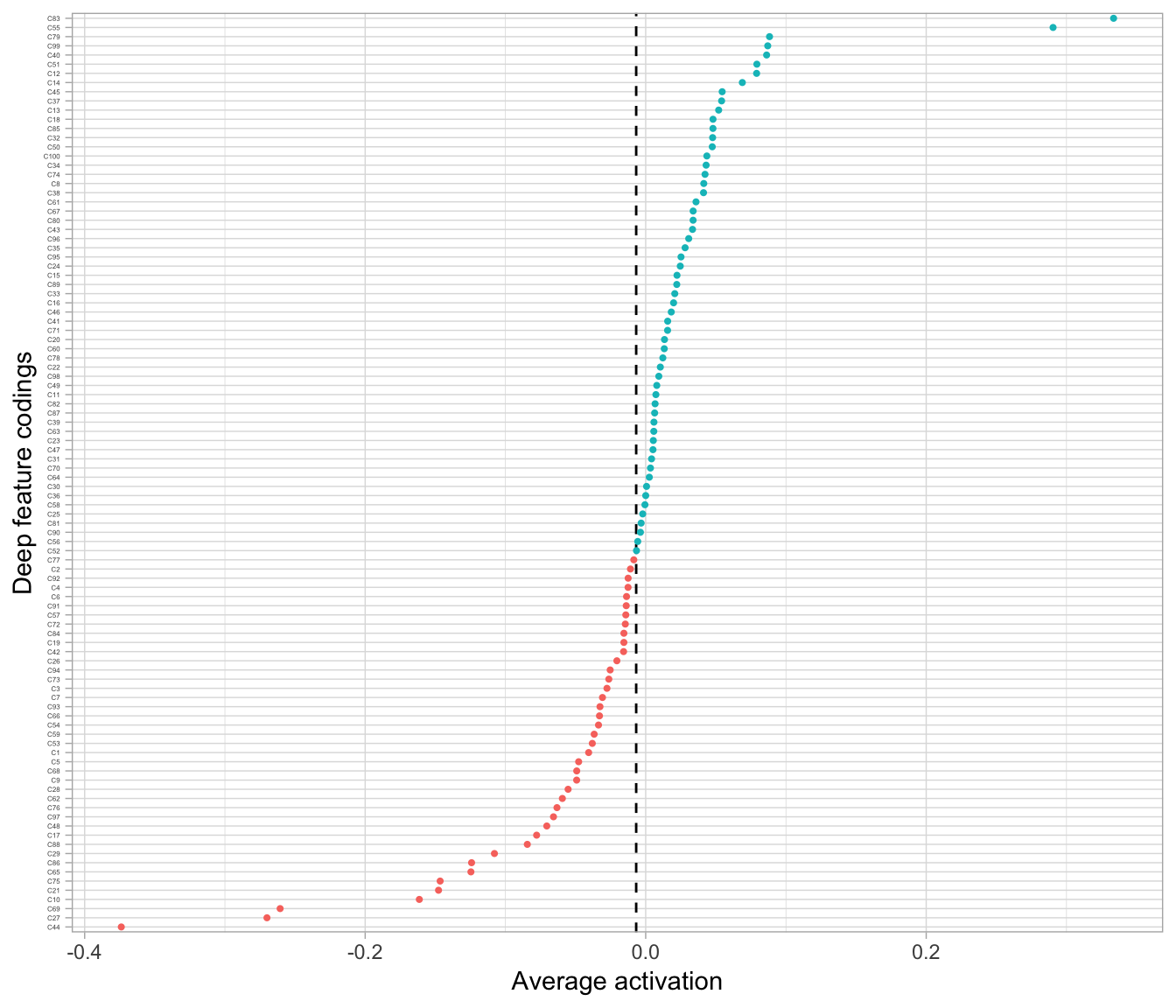

The most commonly used penalty is known as the Kullback-Leibler divergence (KL divergence) which measure the divergence between the target probability $\rho$ that a neuron in the coding layer will activate, and the actual probability.

$$\sum \sum \text{KL} (\rho||\hat{\rho}) = \sum \rho \log{\frac{\rho}{\hat{\rho}}} + (1 - \rho) \log{\frac{1-\rho}{1-\hat{\rho}}}$$

Now we just need to add the penalty to our loss function with a parameter ($\beta$) to control the weight of the penalty.

$$\text{minimize} \left( L = f(X, X') + \beta \sum \text{KL} (\rho||\hat{\rho}) \right)$$

Adding sparsity can force the model to represent each input as a combination of a smaller number of activations.

19.6.2 Tuning sparsity $\beta$ parameter

1. Defining an evaluation grid for the $\beta$ parameter.

hyper_grid <- list(sparsity_beta = c(0.01, 0.05, 0.1, 0.2))

2. Training a model for each option

ae_sparsity_grid <- h2o.grid(
  algorithm = 'deeplearning',
  x = seq_along(features),
  training_frame = features,
  grid_id = 'sparsity_grid',
  autoencoder = TRUE,
  hidden = 100,
  activation = 'Tanh',
  hyper_params = hyper_grid,
  sparse = TRUE,
  average_activation = -0.1,
  ignore_const_cols = FALSE,
  seed = 123
)

3. Identifying the best option.

h2o.getGrid('sparsity_grid', sort_by = 'mse', decreasing = FALSE)
## H2O Grid Details
## ================
## 
## Grid ID: sparsity_grid 
## Used hyper parameters: 
##   -  sparsity_beta 
## Number of models: 4 
## Number of failed models: 0 
## 
## Hyper-Parameter Search Summary: ordered by increasing mse
##   sparsity_beta             model_ids                  mse
## 1          0.01 sparsity_grid_model_1 0.012982916169006953
## 2           0.2 sparsity_grid_model_4  0.01321464889160263
## 3          0.05 sparsity_grid_model_2  0.01337749148043942
## 4           0.1 sparsity_grid_model_3 0.013516631653257992