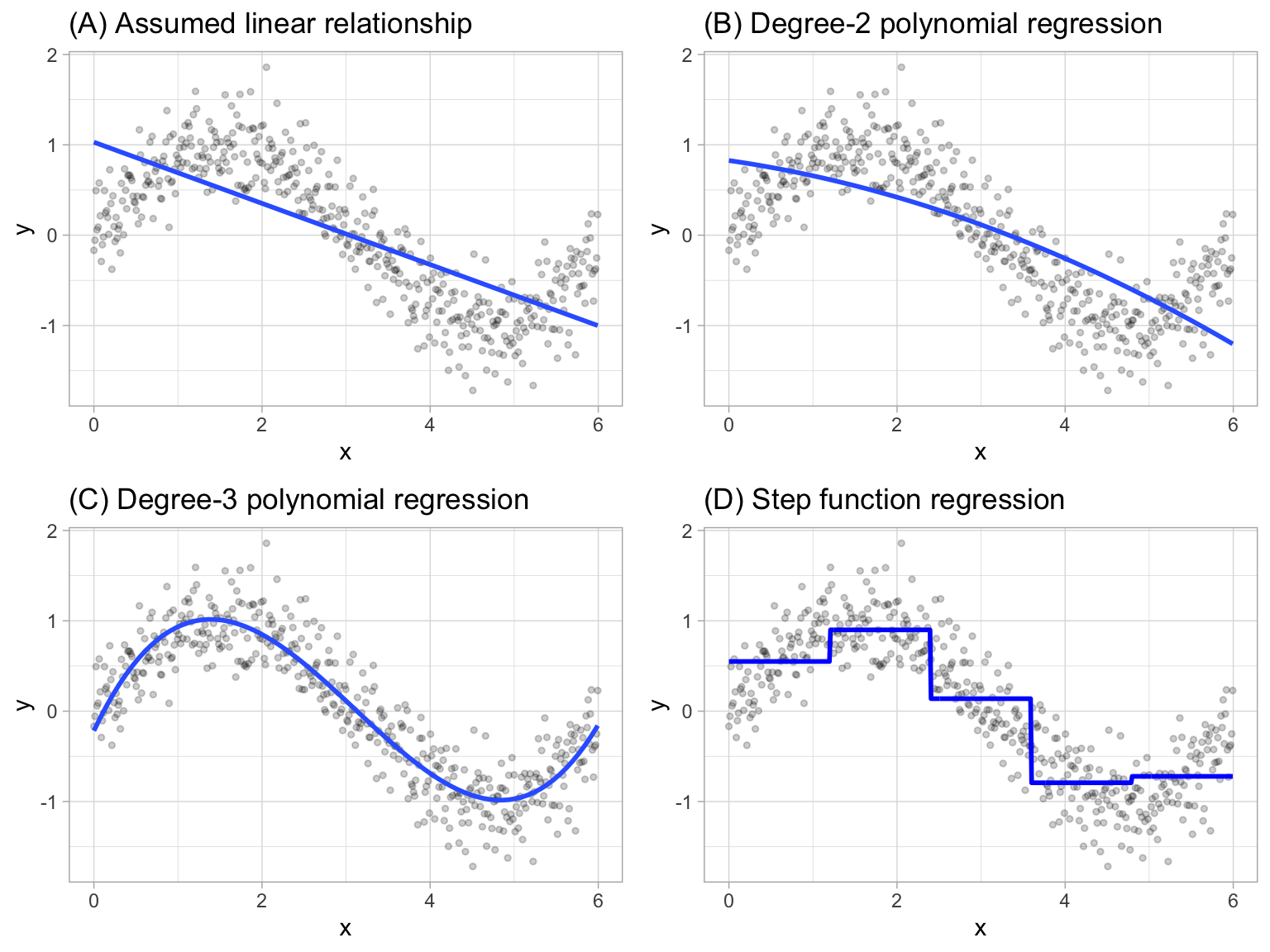
Extending linear models

• Polynomial regression: It extends the linear model by adding extra predictors, obtained by raising each of the original predictors to a power. Generally speaking, it is unusual to use $d$ greater than 3 or 4 as the larger $d$ becomes, the easier the function fit becomes overly flexible and oddly shaped as it tends to increase the presence of multicollinearity.

$$y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \beta_3 x_i^3 + \dots + \beta_d x_i^d + \epsilon_i$$

• Piecewise constant regression: It’s a step function which breaks the range of $X$ into bins and fit a simple constant (e.g., the mean response) in each bin.

If we define the cutpoints as $c_1, c_2, \dots, c_K$ in the range of X, we can create dummy variables to represent each range. For example, if $c_1 \leq x_i < c_2$ is TRUE then $C_1(x_i) = 1$ and then we need to repeat that process for each value of $X$ and range. As result we can fit a lineal regression based on the new variables.

$$y_i = \beta_0 + \beta_1 C_1(x_i) + \beta_2 C_2(x_i) \dots + \beta_K C_K(x_i) + \epsilon_i$$