6.6 - Attrition data

We saw that regularization significantly improved our predictive accuracy for the Ames data set, but how about for the employee attrition example from Chapter 5?

attrition <- modeldata::attrition

df <- attrition %>% mutate_if(is.ordered, factor, ordered = FALSE)

# Create training (70%) and test (30%) sets for the
# rsample::attrition data. Use set.seed for reproducibility
set.seed(123)
churn_split <- initial_split(df, prop = .7, strata = "Attrition")
train <- training(churn_split)
test  <- testing(churn_split)

# train logistic regression model (no regularization)
set.seed(123)
glm_mod <- train(
  Attrition ~ ., 
  data = train, 
  method = "glm",
  family = "binomial",
  preProc = c("zv", "center", "scale"),
  trControl = trainControl(method = "cv", number = 10)
  )

# evaluation metrics
glm_mod$results

##   parameter  Accuracy     Kappa AccuracySD   KappaSD
## 1      none 0.8715662 0.4539185 0.03610858 0.1452058

# number of coefficients
length(glm_mod$coefnames)

## [1] 57

# train regularized logistic regression model
set.seed(123)
penalized_mod <- train(
  Attrition ~ ., 
  data = train, 
  method = "glmnet",
  family = "binomial",
  preProc = c("zv", "center", "scale"),
  trControl = trainControl(method = "cv", number = 10),
  tuneLength = 10
  )

# evaluation metrics
penalized_mod$resample$Accuracy

##  [1] 0.8349515 0.8653846 0.8823529 0.8349515 0.9223301 0.8823529 0.8834951
##  [8] 0.8725490 0.9126214 0.9029126

penalized_mod$resample$Kappa

##  [1] 0.2343682 0.2639029 0.4035088 0.1912240 0.6281588 0.4035088 0.4467323
##  [8] 0.4137931 0.5974815 0.5657673

# number of coefficients
length(penalized_mod$coefnames)

## [1] 57

# extract out of sample performance measures
accuracy_list <- summary(resamples(list(
  logistic_model = glm_mod, 
  penalized_model = penalized_mod
  )))$statistics$Accuracy

accuracy_list

##                      Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
## logistic_model  0.8058252 0.8529412 0.8786765 0.8715662 0.8907767 0.9320388
## penalized_model 0.8349515 0.8671757 0.8823529 0.8793902 0.8980583 0.9223301
##                 NA's
## logistic_model     0
## penalized_model    0

# accuracy boxplot
accuracy_df <- as.data.frame(accuracy_list)

accuracy_df %>%
     select(-7) %>%
     rownames_to_column() %>%
     rename(.model = rowname) %>%
     pivot_longer(-.model) %>% 
     
     ggplot(aes(.model, value, fill = .model)) + 
     geom_boxplot(show.legend = FALSE) + 
     scale_y_continuous(labels = scales::percent) + 
     labs(x = NULL, 
          y = 'Accuracy (%)')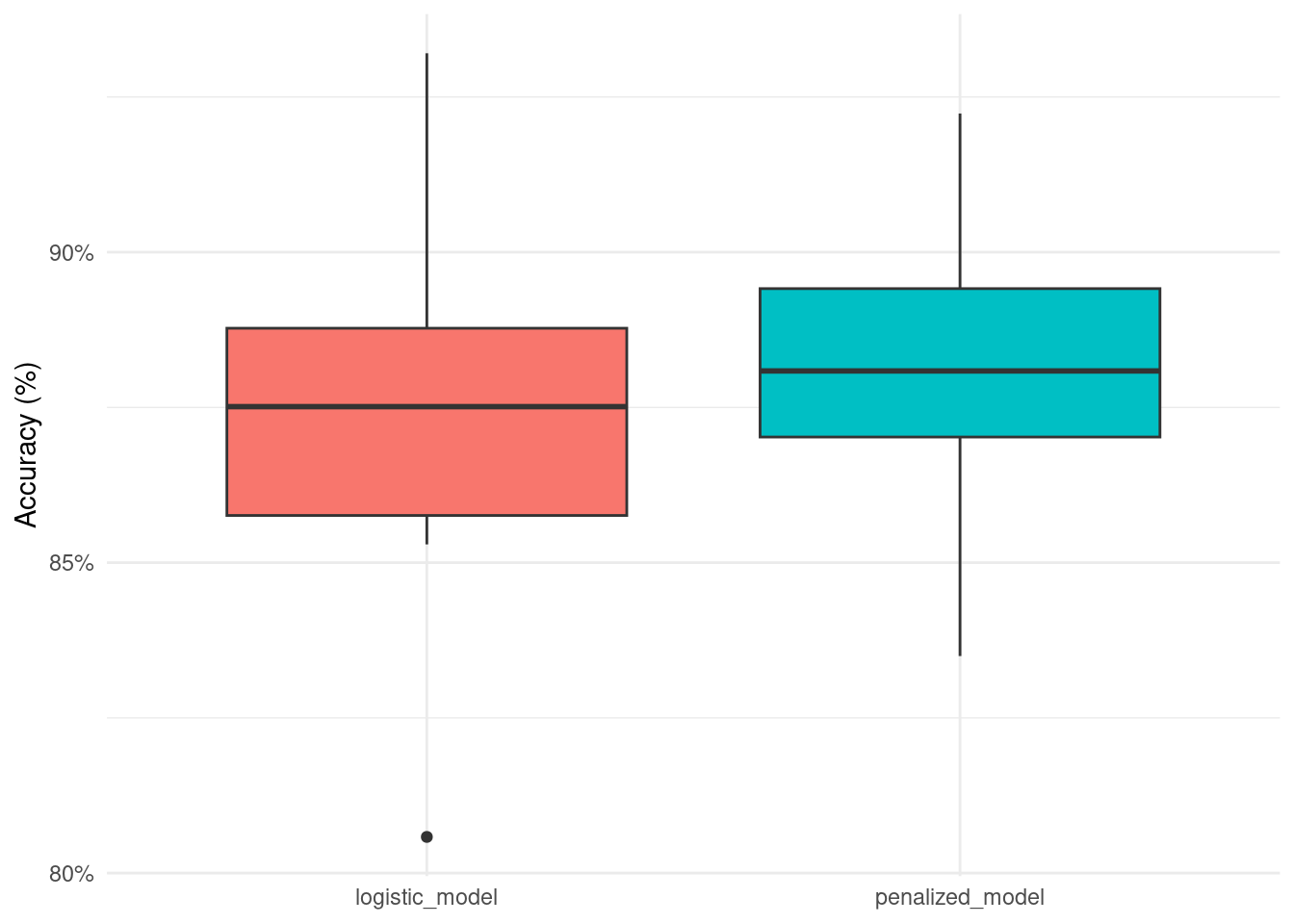

# t-test
accuracy_long_df <- accuracy_df %>%
     select(-7) %>%
     # rownames_to_column() %>%
     # rename(.model = rowname) %>% 
     t() %>% 
     as.data.frame()

rownames(accuracy_long_df) <- 1:nrow(accuracy_long_df)

t.test(accuracy_long_df$logistic_model, accuracy_long_df$penalized_model)

## 
##  Welch Two Sample t-test
## 
## data:  accuracy_long_df$logistic_model and accuracy_long_df$penalized_model
## t = -0.41886, df = 8.9681, p-value = 0.6852
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.05596183  0.03848384
## sample estimates:
## mean of x mean of y 
## 0.8719708 0.8807098

# kappa
kappa_list <- summary(resamples(list(
     logistic_model = glm_mod, 
     penalized_model = penalized_mod
)))$statistics$Kappa

kappa_list

##                      Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
## logistic_model  0.2605887 0.3422335 0.4471863 0.4539185 0.5641394 0.7031700
## penalized_model 0.1912240 0.2988044 0.4086509 0.4148446 0.5360085 0.6281588
##                 NA's
## logistic_model     0
## penalized_model    0

# kappa boxplot
kappa_df <- as.data.frame(kappa_list)

kappa_df %>%
     select(-7) %>%
     rownames_to_column() %>%
     rename(.model = rowname) %>%
     pivot_longer(-.model) %>% 
     
     ggplot(aes(.model, value, fill = .model)) + 
     geom_boxplot(show.legend = FALSE) + 
     scale_y_continuous(labels = scales::percent) + 
     labs(x = NULL, 
          y = 'Kappa (%)')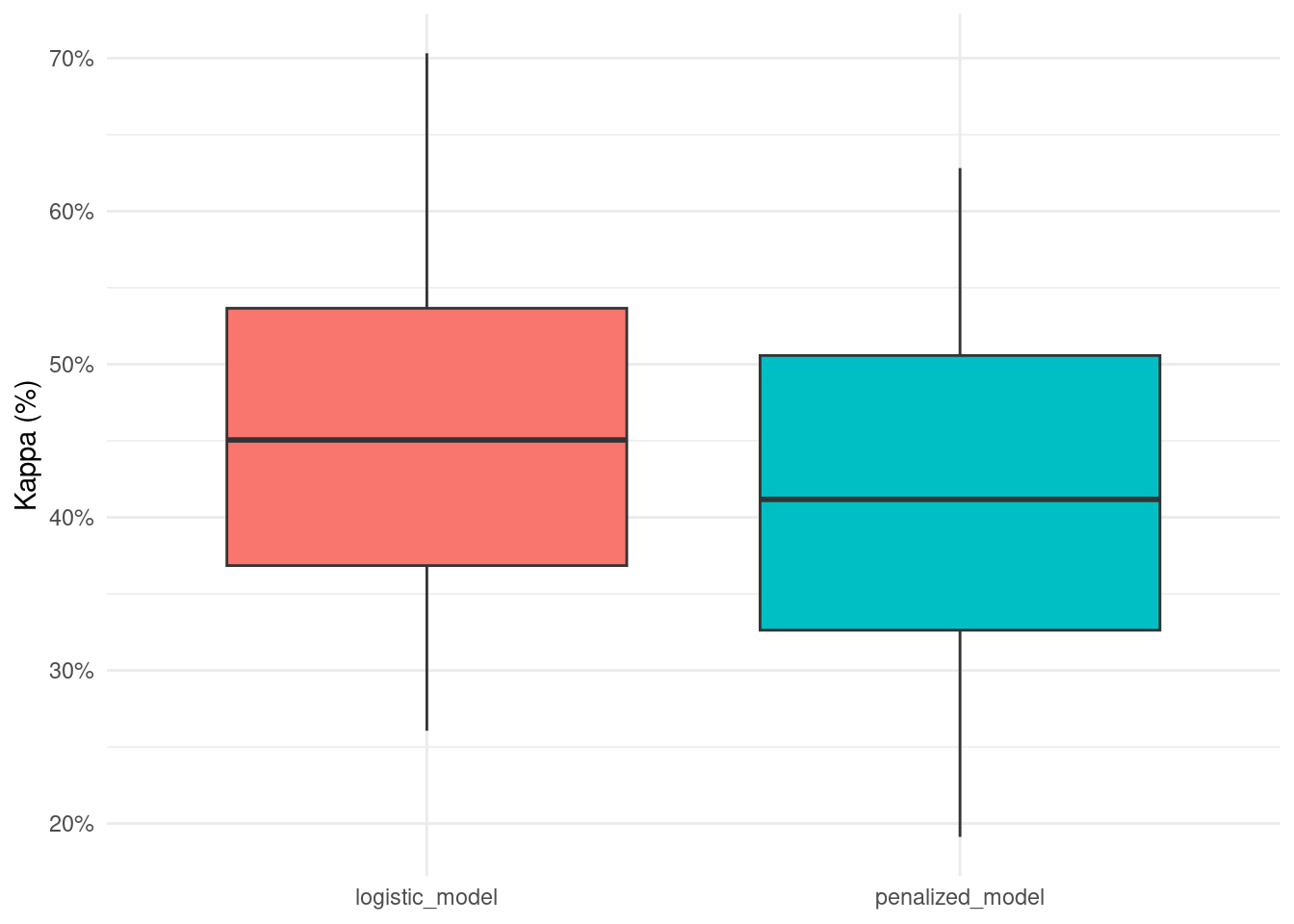

# t-test
kappa_long_df <- kappa_df %>%
     select(-7) %>%
     # rownames_to_column() %>%
     # rename(.model = rowname) %>% 
     t() %>% 
     as.data.frame()

rownames(kappa_long_df) <- 1:nrow(kappa_long_df)

t.test(kappa_long_df$logistic_model, kappa_long_df$penalized_model)

## 
##  Welch Two Sample t-test
## 
## data:  kappa_long_df$logistic_model and kappa_long_df$penalized_model
## t = 0.53868, df = 10, p-value = 0.6019
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.1534413  0.2512897
## sample estimates:
## mean of x mean of y 
## 0.4618727 0.4129486