6.2.1 - Ridge penalty

Ridge (L2) regression controls the estimated coefficients by adding a penalty to the objective function:

\[\begin{equation} \operatorname{minimize}\left(S S E+\lambda \sum_{j=1}^p \beta_j^2\right) \end{equation}\]

• When \(\lambda\) = 0, there is no effect and the objective function is equal to the OLS regression.

• However, as \(\lambda\) -> \(\infty\), the penalty becomes large and forces the coefficients toward zero (but not all the way).

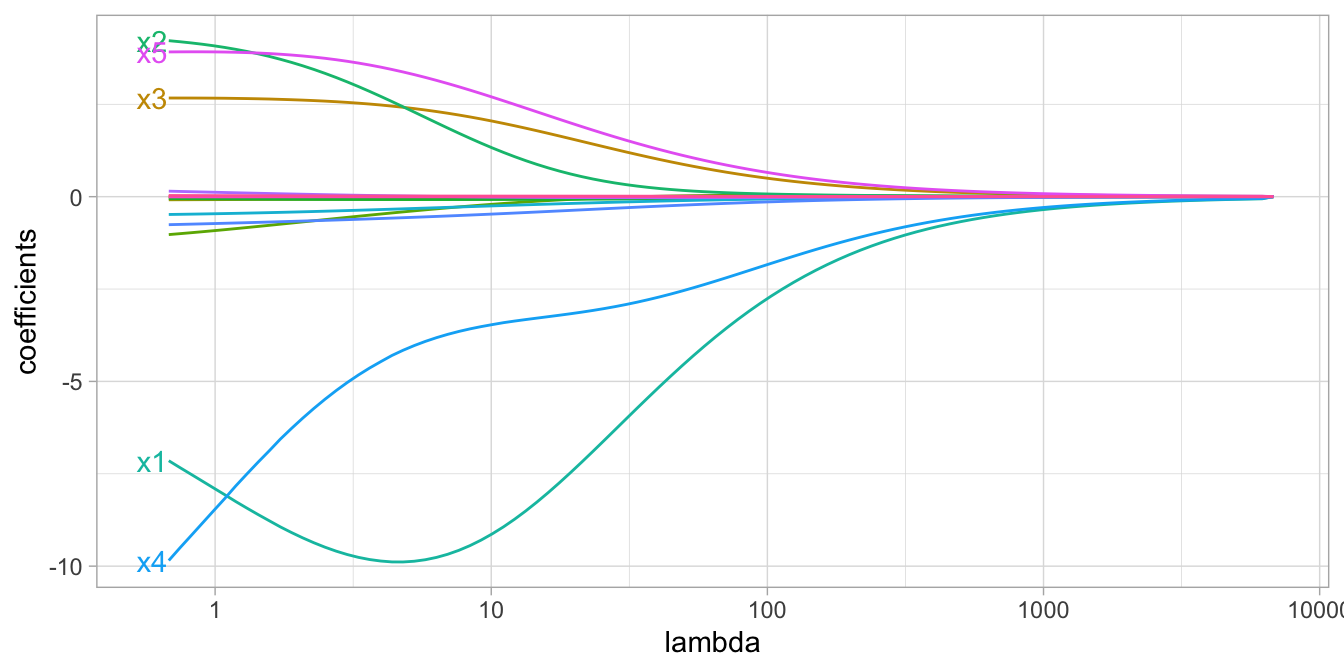
Figure 6.2: Ridge regression coefficients for 15 exemplar predictor variables as λ grows from 0→∞. As λ grows larger, our coefficient magnitudes are more constrained.

• Ridge regression does not perform feature selection and will retain all available features.