Explaning the model

MARS is an algorithm that automatically creates a piecewise linear model after grasping the concept of multiple linear regression.

It will first look for the single point across the range of $X$ values where two different linear relationships between $Y$ and $X$ achieve the smallest error (e.g., Sum of Squares Error). What results is known as a hinge function $h(x-a)$, where $a$ is the cutpoint value (knot).

For example, let’s use $1.183606$ the our first knot.

$$y = \begin{cases} \beta_0 + \beta_1(1.183606 - x) & x < 1.183606, \\ \beta_0 + \beta_1(x - 1.183606) & x < 1.183606 \\ \end{cases}$$

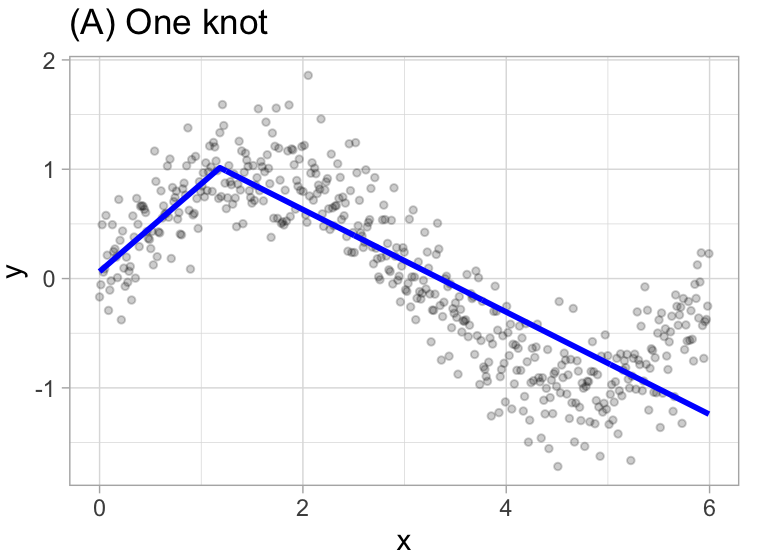
Once the first knot has been found, the search continues for a second knot.

$$y = \begin{cases} \beta_0 + \beta_1(1.183606 - x) & x < 1.183606, \\ \beta_0 + \beta_1(x - 1.183606) & x < 1.183606 \quad \& \quad x < 4.898114 \\ \beta_0 + \beta_1(4.898114 - x) & x > 4.898114 \end{cases}$$

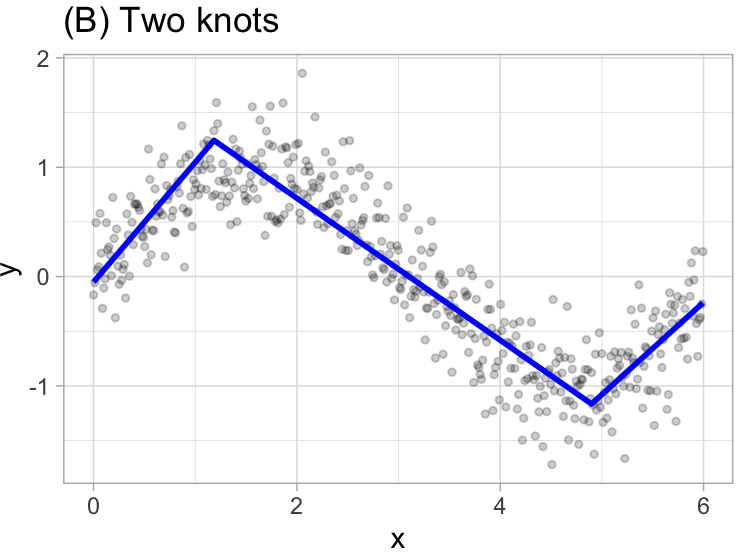
This procedure continues until $R^2$ change by less than 0.001.

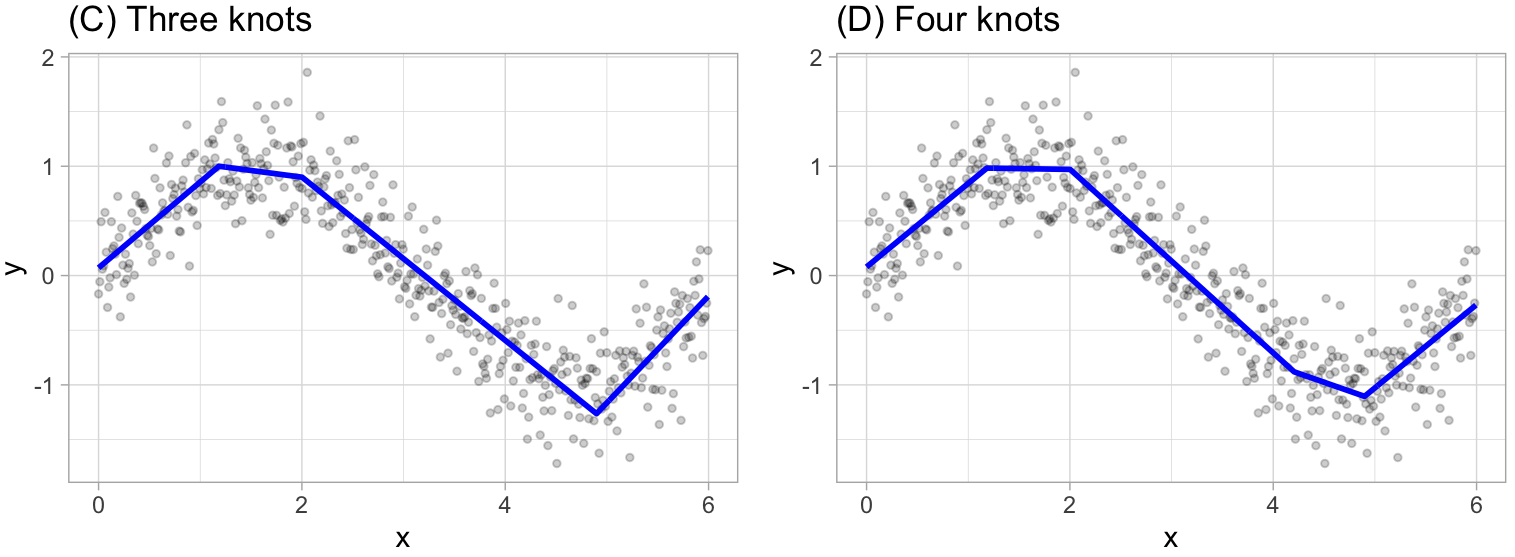
Then the model starts the pruning process, which consist in using cross-validation to remove knots that do not contribute significantly to predictive accuracy. To be more specific the package used in R performs a Generalized cross-validation which is a shortcut for linear models that produces an approximate leave-one-out cross-validation error metric.