6.2.2 - Lasso penalty
The lasso (least absolute shrinkage and selection operator) penalty is an alternative to the ridge penalty that requires only a small modification. The objective function is:
\[\begin{equation} \operatorname{minimize}\left(S S E+\lambda \sum_{j=1}^p |\beta_j|\right) \end{equation}\]Whereas the ridge penalty pushes variables to approximately but not equal to zero, the lasso penalty will actually push coefficients all the way to zero as illustrated in Figure 6.3.
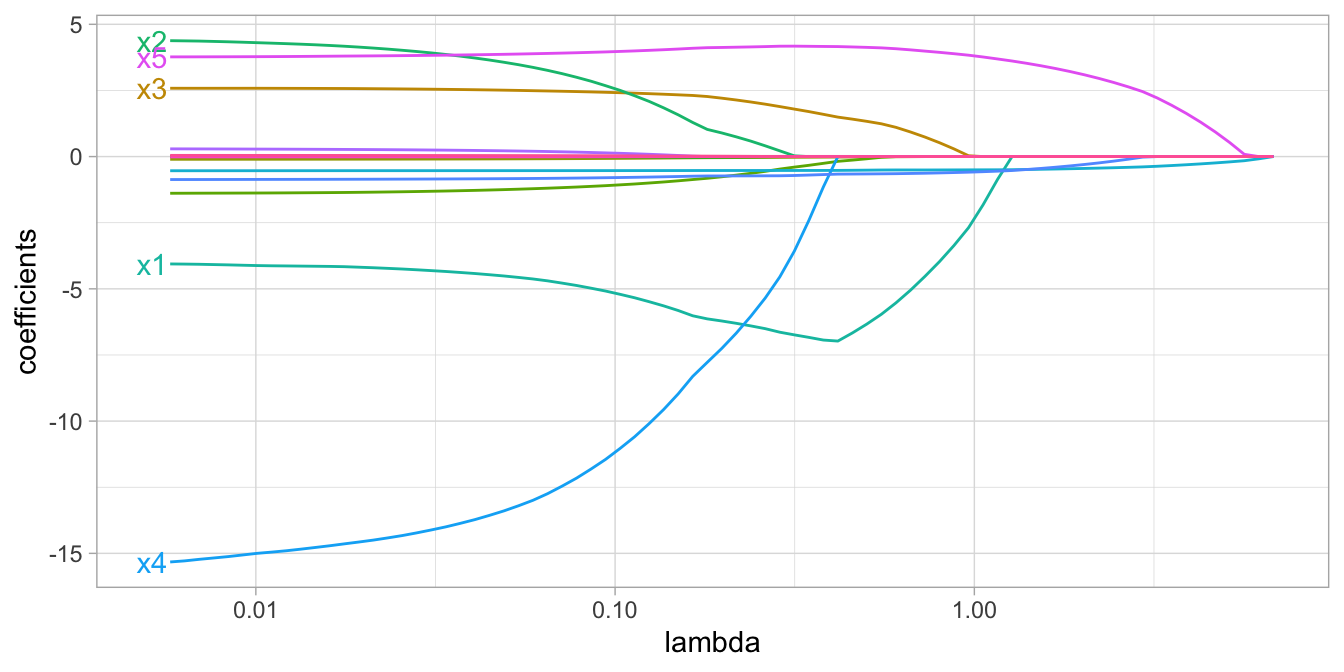
Figure 6.3: Lasso regression coefficients as λ grows from 0→∞.
In the figure above we see that when λ<0.01 all 15 variables are included in the model, when λ≈0.5 9 variables are retained, and when log(λ)=1 only 5 variables are retained.