3.2 Time series components

Time series are made of three components:

  • a trend-cycle component \(T_t\)
  • a seasonal component \(S_t\)
  • a remainder component \(R_t\)

3.2.1 Additive decomposition

When the variation around the trend-cycle does not vary with the level of the time series.

\[y_t=S_t+T_t+R_t\]

3.2.2 Multiplicative decomposition

When the variation in the seasonal pattern, or the variation around the trend-cycle, appears to be proportional to the level of the time series.

\[y_t=S_t*T_t*R_t\] An alternative can be a log transformation

\[log(y_t)=log(S_t)+log(T_t)+log(R_t)\]

3.2.3 Example: Employment in the US retail sector

A nice introduction to the use of the {fpp3} package by the author is in the section Example at minute 13.11 here: Dr. Rob J. Hyndman - Ensemble Forecasts with {fable}

Data

us_employment %>% head()
## # A tsibble: 6 x 4 [1M]
## # Key:       Series_ID [1]
##      Month Series_ID     Title         Employed
##      <mth> <chr>         <chr>            <dbl>
## 1 1939 Jan CEU0500000001 Total Private    25338
## 2 1939 Feb CEU0500000001 Total Private    25447
## 3 1939 Mar CEU0500000001 Total Private    25833
## 4 1939 Apr CEU0500000001 Total Private    25801
## 5 1939 May CEU0500000001 Total Private    26113
## 6 1939 Jun CEU0500000001 Total Private    26485

3.2.3.1 STL decomposition method

Seasonal and Trend decomposition using Loess.

STL produces a smoother trend than classical decomposition methods due to the use of local polynomial regression.

Some interesting information about the STL model:

  • it is additive
  • it is iterative and relies on the alternate estimation of the trend
  • the seasonal components are locally estimated scatterplot smoothing (Loess)
  • it estimates nonlinear relationships
  • the seasonal component is allowed to change over time
  • it is composed of seasonal patterns estimated based on k consecutive seasonal cycles
  • k controls how rapidly the seasonal component can change
  • it is robust to outliers and missing data
  • it is able to decompose time series with seasonality of any frequency, and provides implementation using numerical methods instead of mathematical modeling.

More info here: R. B. Cleveland et al. (1990)

from the book

The command used is:

 model(stl = STL(<formula>))
us_employment%>% #year(Month) >= 1990, 
  filter(Title == "Retail Trade") %>%
  select(-Series_ID) %>%
  autoplot()
## Plot variable not specified, automatically selected `.vars = Employed`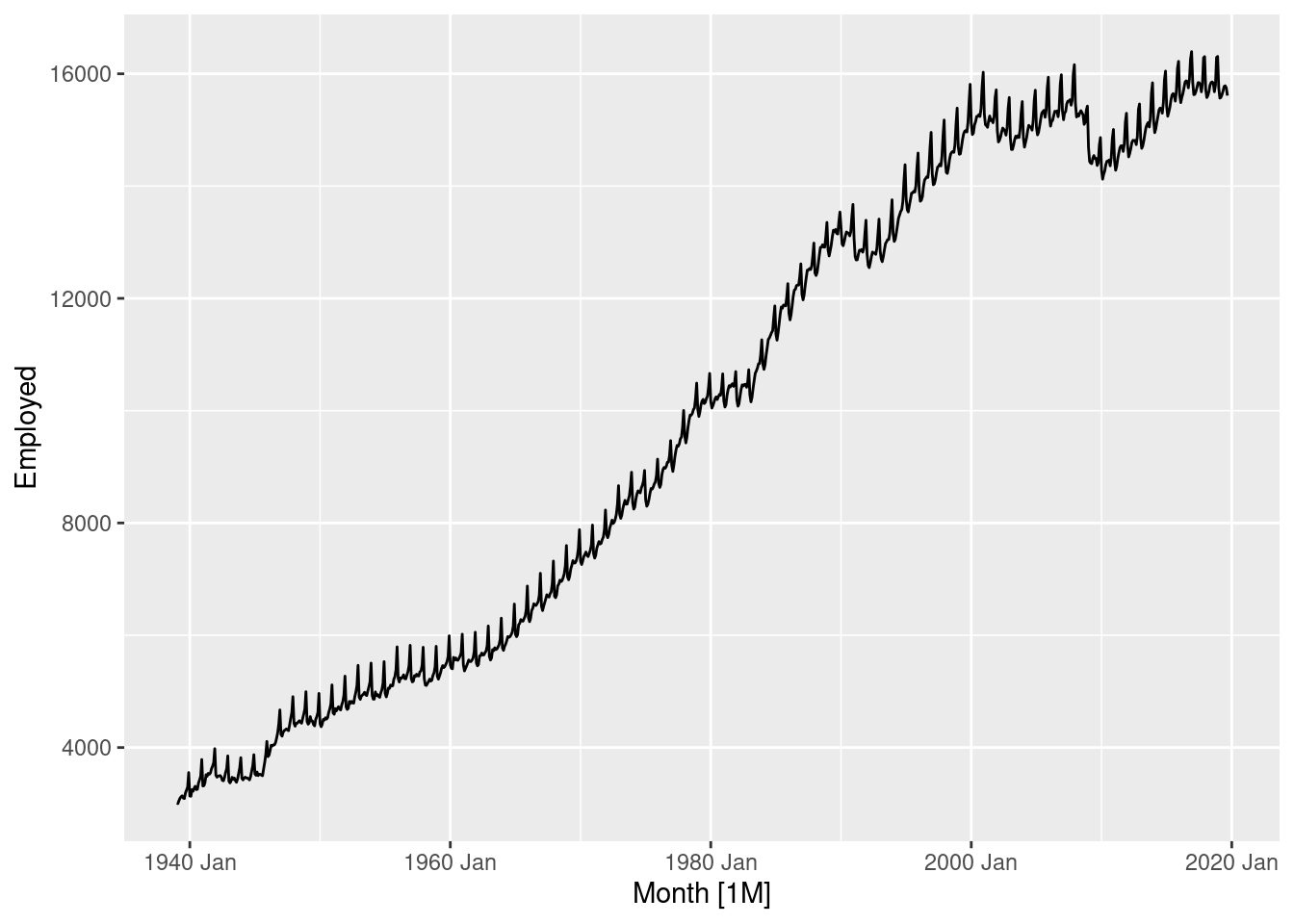

us_retail_employment <- us_employment %>%
  filter(year(Month) >= 1990, Title == "Retail Trade") %>%
  select(-Series_ID)


dcmp <- us_retail_employment %>%
  model(stl = STL(Employed))


components(dcmp) %>%
  autoplot()+
  ggthemes::theme_pander()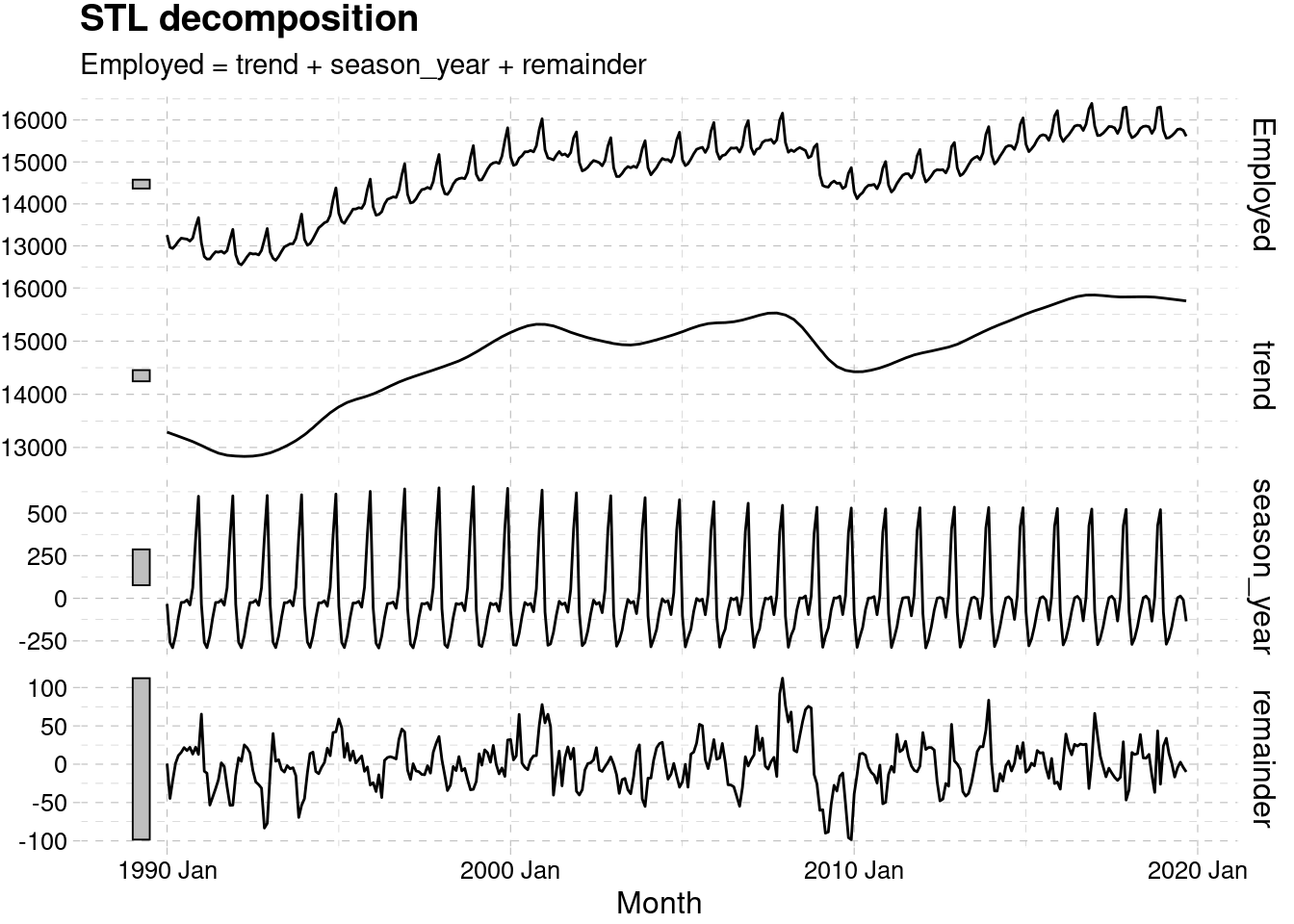

?components
methods("components")
components(dcmp) %>%
  as_tsibble()%>%
  select(Month,Employed,trend,season_adjust,remainder)%>%
  head
## # A tsibble: 6 x 5 [1M]
##      Month Employed  trend season_adjust remainder
##      <mth>    <dbl>  <dbl>         <dbl>     <dbl>
## 1 1990 Jan   13256. 13288.        13289.     0.836
## 2 1990 Feb   12966. 13269.        13224.   -44.6  
## 3 1990 Mar   12938. 13250.        13228.   -22.1  
## 4 1990 Apr   13012. 13231.        13232.     1.05 
## 5 1990 May   13108. 13211.        13223.    11.3  
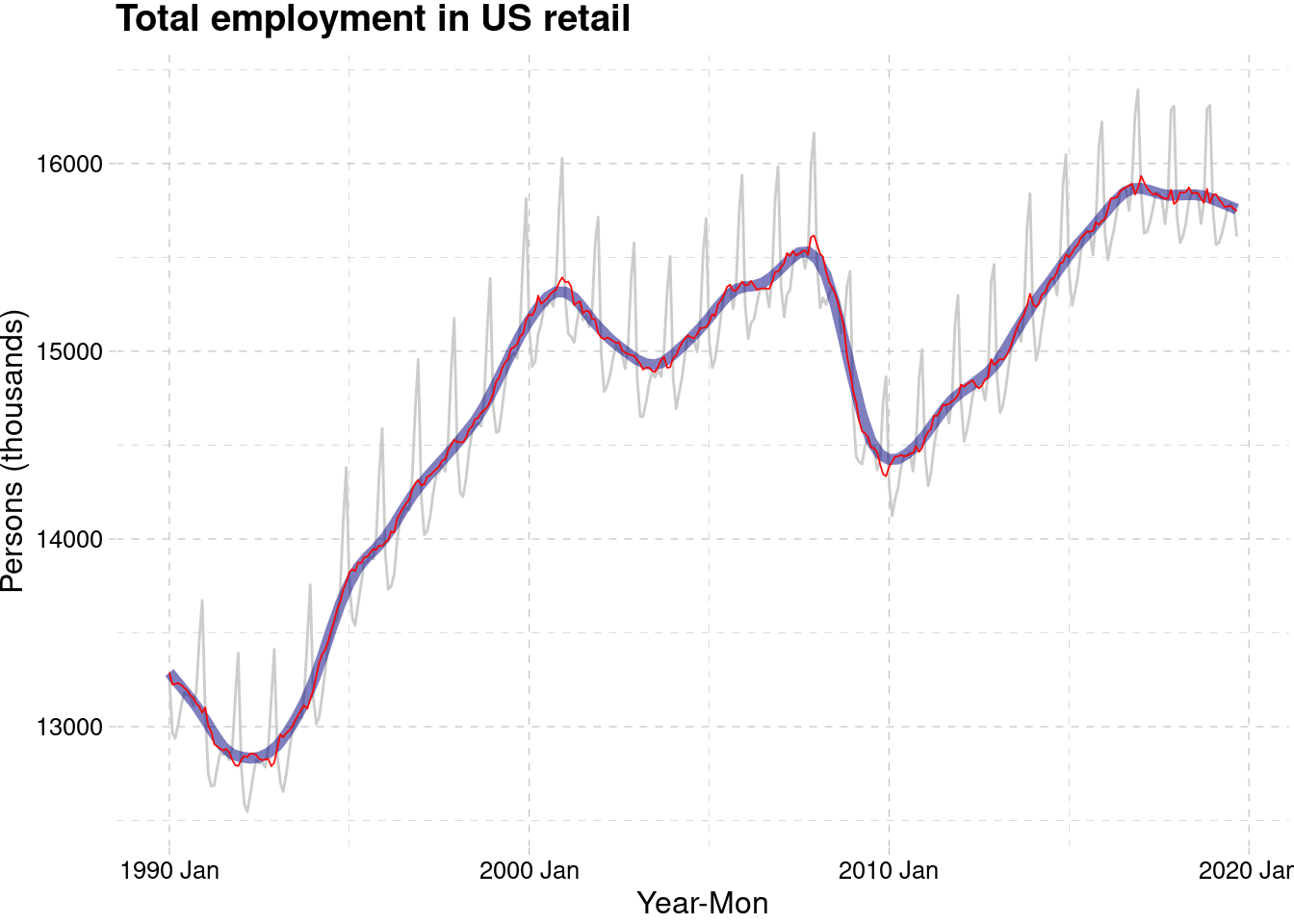
## 6 1990 Jun   13183. 13192.        13207.    15.5
components(dcmp) %>%
  as_tsibble() %>%
  autoplot(Employed, colour="grey80") +
  geom_line(aes(y=trend), colour = "navy",linewidth=2,alpha=0.5) +
  geom_line(aes(y=season_adjust), colour = "red",linewidth=0.3) +
  # geom_line(aes(y=remainder), colour = "blue") +
  labs(y = "Persons (thousands)",x="Year-Mon",
       title = "Total employment in US retail")+
  ggthemes::theme_pander()