3.3 Classical decompositions
A classical decomposition method is the moving average method to estimate the trend-cycle. It originated in the 1920s and was widely used until the 1950s.
3.3.1 Moving average smoothing
A moving average of order m: seasonal period
\[m=2k+1\]
composed of seasonal patterns estimated based on k consecutive seasonal cycles, where \(k\) controls how rapidly the component can change.
The estimate of the trend-cycle at time \(t\) is obtained by averaging values of the time series within \(k\) periods of \(t\).
the average eliminates some of the randomness
\[\hat{T_t}=\frac{1}{m}\sum_{j=-k}^k{y_{t+j}}\]
aus_exports <- global_economy %>%
filter(Country == "Australia")%>%
mutate(`3-MA` = slider::slide_dbl(Exports, mean,
.before = 1, # this is k
.after = 1,
.complete = TRUE),
`5-MA` = slider::slide_dbl(Exports, mean,
.before = 2, # this is k
.after = 2,
.complete = TRUE),
`7-MA` = slider::slide_dbl(Exports, mean,
.before = 3, # this is k
.after = 3,
.complete = TRUE),
`9-MA` = slider::slide_dbl(Exports, mean,
.before = 4, # this is k
.after = 4,
.complete = TRUE)
) %>%
select(Year,Exports,`3-MA`,`5-MA`,`7-MA`,`9-MA`)%>%
pivot_longer(cols = ends_with("MA"),names_to = "kma",values_to="values")
aus_exports %>% head## # A tsibble: 6 x 4 [1Y]
## # Key: kma [4]
## Year Exports kma values
## <dbl> <dbl> <chr> <dbl>
## 1 1960 13.0 3-MA NA
## 2 1960 13.0 5-MA NA
## 3 1960 13.0 7-MA NA
## 4 1960 13.0 9-MA NA
## 5 1961 12.4 3-MA 13.1
## 6 1961 12.4 5-MA NAaus_exports %>%
autoplot(Exports,color="darkred",size=0.2) +
geom_line(aes(y = values,color=kma)) +
labs(y = "% of GDP",x="Year",
title = "Total Australian exports") +
guides(colour = guide_legend(title = "series"))+
ggthemes::scale_color_pander()+
ggthemes::theme_pander()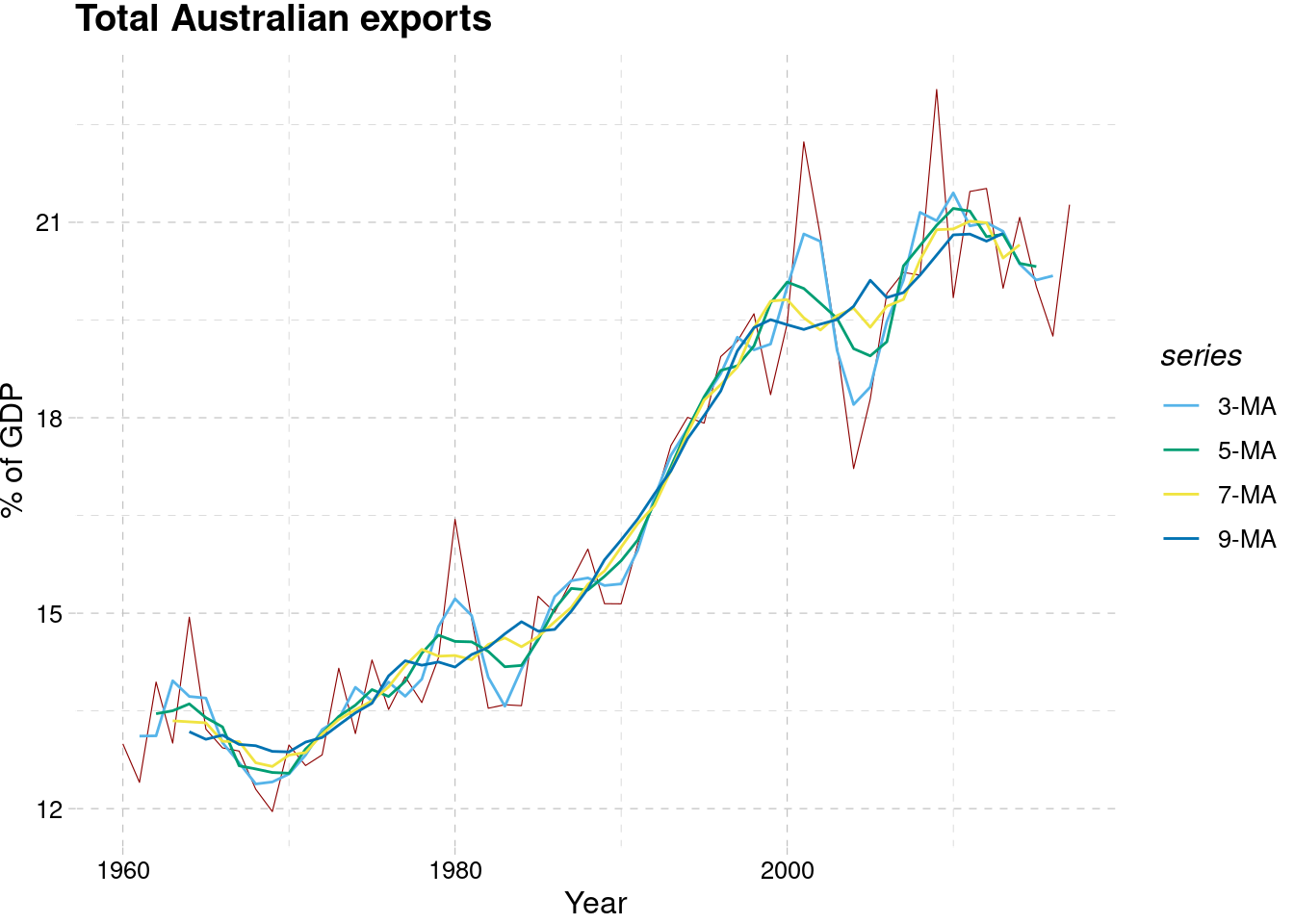
3.3.2 Moving averages of moving averages
When 2-MA follows a moving average of an even order (such as 4), it is called a “centered moving average of order 4”
The most common use of centred moving averages is for estimating the trend-cycle from seasonal data.
beer_ma <- aus_production %>%
filter(year(Quarter) >= 1992) %>%
select(Quarter, Beer) %>%
mutate(`4-MA` = slider::slide_dbl(Beer, mean,
.before = 1, .after = 2, .complete = TRUE),
`2x4-MA` = slider::slide_dbl(`4-MA`, mean,
.before = 1, .after = 0, .complete = TRUE)
)
beer_ma %>%head## # A tsibble: 6 x 4 [1Q]
## Quarter Beer `4-MA` `2x4-MA`
## <qtr> <dbl> <dbl> <dbl>
## 1 1992 Q1 443 NA NA
## 2 1992 Q2 410 451. NA
## 3 1992 Q3 420 449. 450
## 4 1992 Q4 532 452. 450.
## 5 1993 Q1 433 449 450.
## 6 1993 Q2 421 444 446.3.3.3 Weighted moving averages
Combinations of moving averages result in weighted moving averages.
Weights: \(a_k=[\frac{1}{8},\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{8}]\)
k: \(k=(m-1)/2\)
\[\hat{T_t}=\sum_{j=-k}^k{a_jy_{t+j}}\]
3.3.4 Additive decomposition
In additive decomposition, it is assumed that the seasonal component is constant from year to year.
\[m=\left\{\begin{matrix} 2\times m-MA & \text{if m is even}\\ m-MA & \text{if m is odd} \end{matrix}\right.\]
De-trend: \(y_t-\hat{T_t}\)
Adjust to ensure that they add to zero
\(R_t=y_t-\hat{T_t}-\hat{S_t}\)
Formula:
?classical_decomposition
model(classical_decomposition(<variable>, type = "additive"))3.3.5 Multiplicative decomposition
For multiplicative seasonality, the \(m\) values that form the seasonal component are sometimes called the “seasonal indices”.
\[m=\left\{\begin{matrix} 2\times m-MA & \text{if m is even}\\ m-MA & \text{if m is odd} \end{matrix}\right.\]
De-trend: \(y_t/\hat{T_t}\)
Adjust to ensure that they add to zero
\(R_t=y_t/(\hat{T_t}\hat{S_t})\)