9.1 Exercise 7

Consider aus_airpassengers, the total number of passengers (in millions) from Australian air carriers for the period 1970-2011.

# load packages
suppressMessages(library(tidyverse))
library(fpp3)
library(plotly)
theme_set(theme_minimal())
# Australia air passengers dataset
aus_airpassengers%>%head
## # A tsibble: 6 x 2 [1Y]
##    Year Passengers
##   <dbl>      <dbl>
## 1  1970       7.32
## 2  1971       7.33
## 3  1972       7.80
## 4  1973       9.38
## 5  1974      10.7 
## 6  1975      11.1
# plot time series
aus_airpassengers %>% 
  autoplot(Passengers) + 
  geom_smooth(method = 'loess', se = FALSE, color = 'steelblue') + 
  labs(title = 'Australia Total Number of Passengers (millions)')
## `geom_smooth()` using formula = 'y ~ x'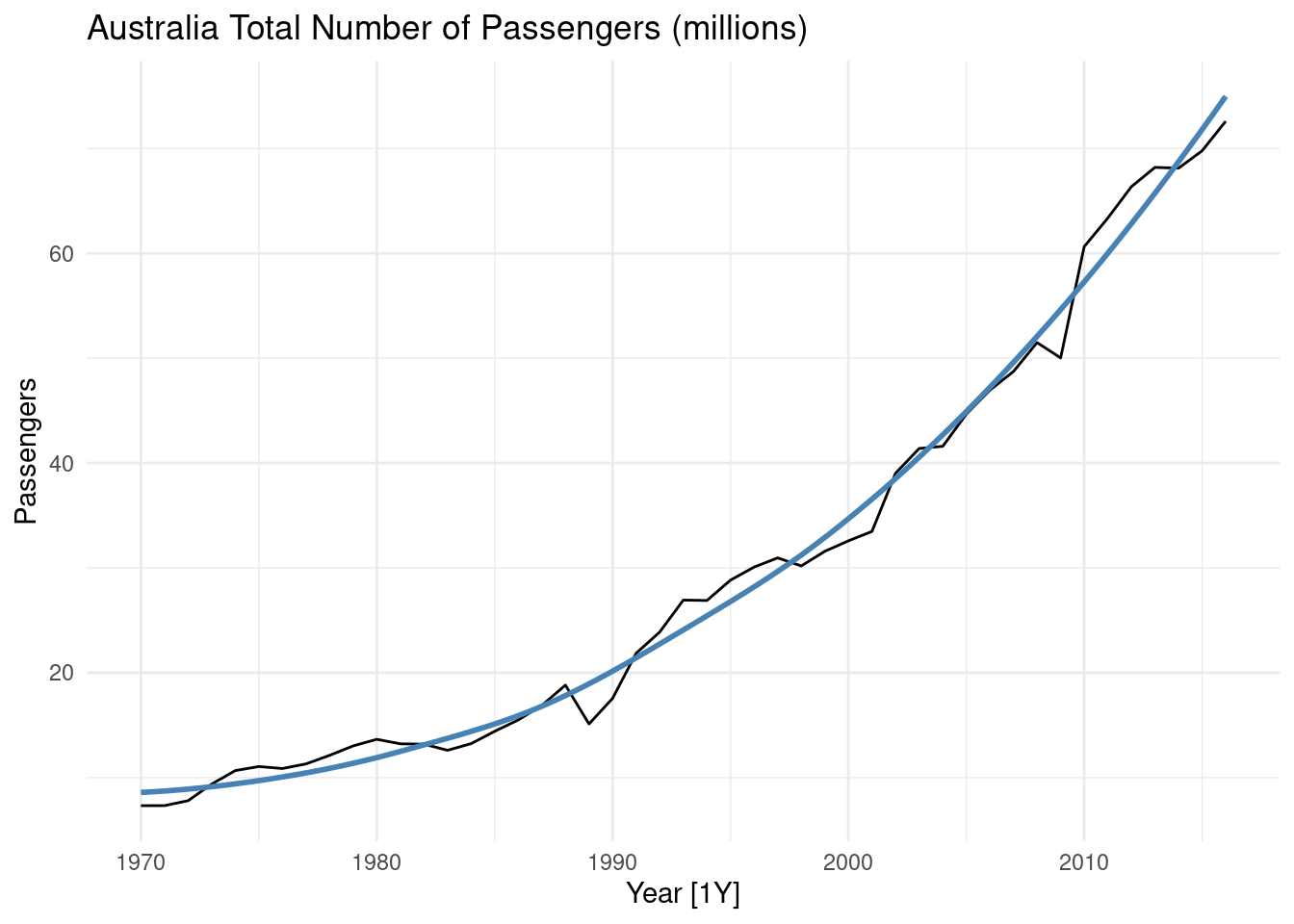

# KPSS test
aus_airpassengers %>% 
  features(Passengers, unitroot_kpss)
## # A tibble: 1 × 2
##   kpss_stat kpss_pvalue
##       <dbl>       <dbl>
## 1      1.19        0.01
# differencing time series
aus_airpassengers %>% 
  mutate(Passengers = Passengers %>% 
           difference(1) %>%
           difference(1)) %>%
  autoplot(Passengers) + 
  labs(title = 'Australia Total Number of Passengers (change)')
## Warning: Removed 2 rows containing missing values or values outside the scale range
## (`geom_line()`).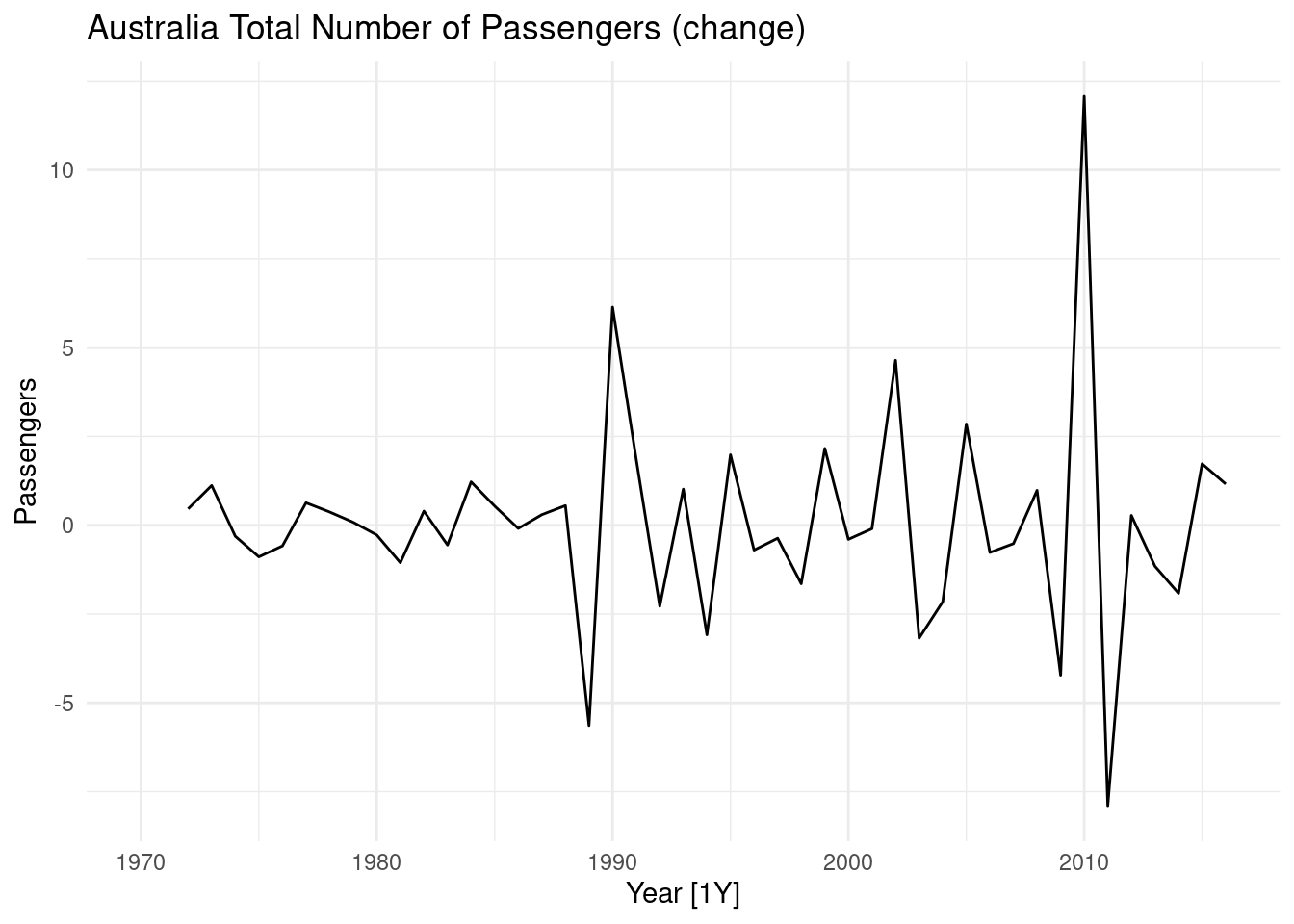

aus_airpassengers %>% 
  mutate(Passengers = Passengers %>% 
           difference(1) %>% 
           difference(1)
  ) %>% 
  features(Passengers, unitroot_kpss)
## # A tibble: 1 × 2
##   kpss_stat kpss_pvalue
##       <dbl>       <dbl>
## 1    0.0361         0.1

9.1.1 a. Use ARIMA() to find an appropriate ARIMA model. What model was selected.

Check that the residuals look like white noise. Plot forecasts for the next 10 periods.

fit_1 <- aus_airpassengers |> 
  model(ARIMA(Passengers))

report(fit_1)
## Series: Passengers 
## Model: ARIMA(0,2,1) 
## 
## Coefficients:
##           ma1
##       -0.8963
## s.e.   0.0594
## 
## sigma^2 estimated as 4.308:  log likelihood=-97.02
## AIC=198.04   AICc=198.32   BIC=201.65
tidy(fit_1)
## # A tibble: 1 × 6
##   .model            term  estimate std.error statistic  p.value
##   <chr>             <chr>    <dbl>     <dbl>     <dbl>    <dbl>
## 1 ARIMA(Passengers) ma1     -0.896    0.0594     -15.1 3.24e-19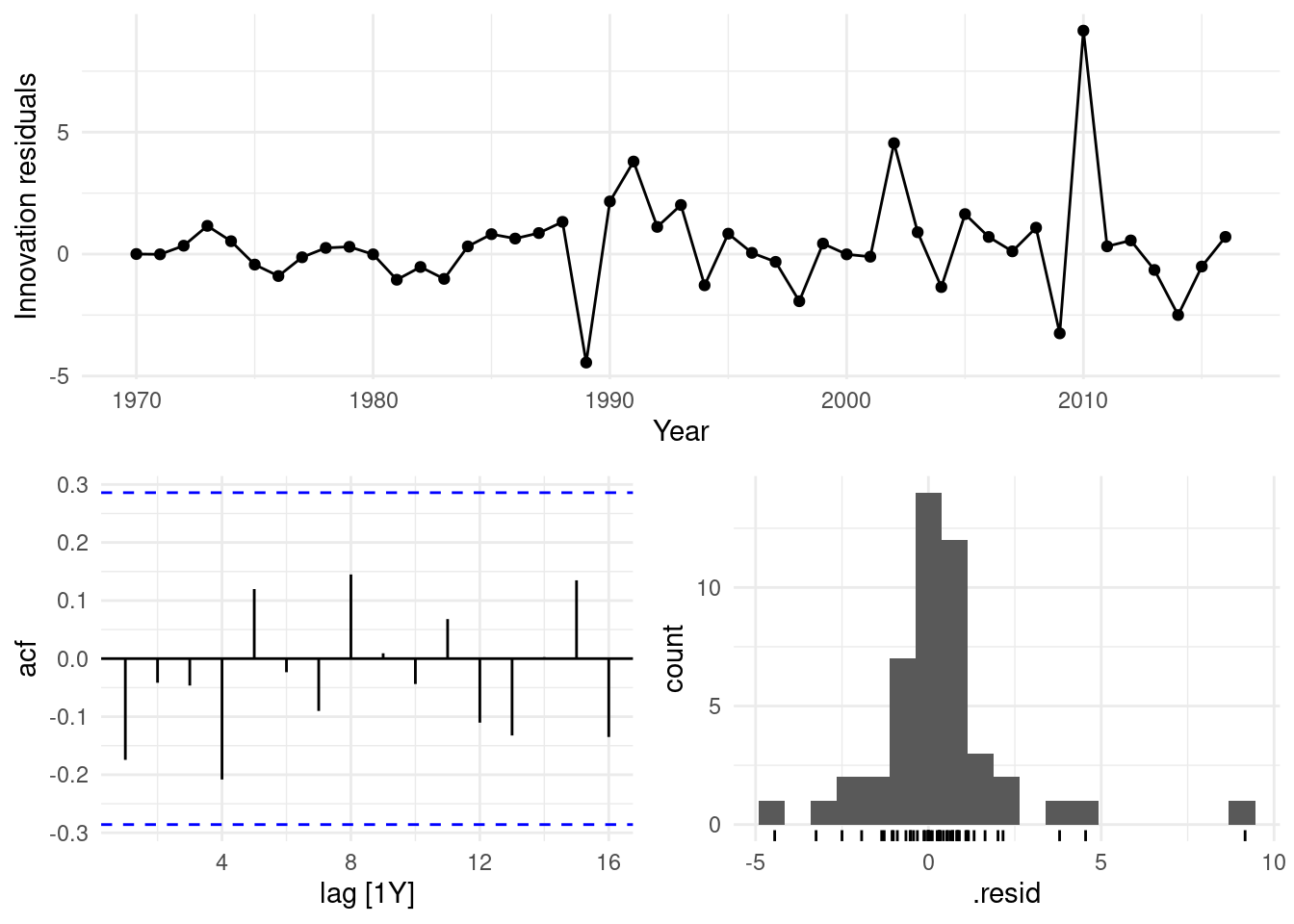
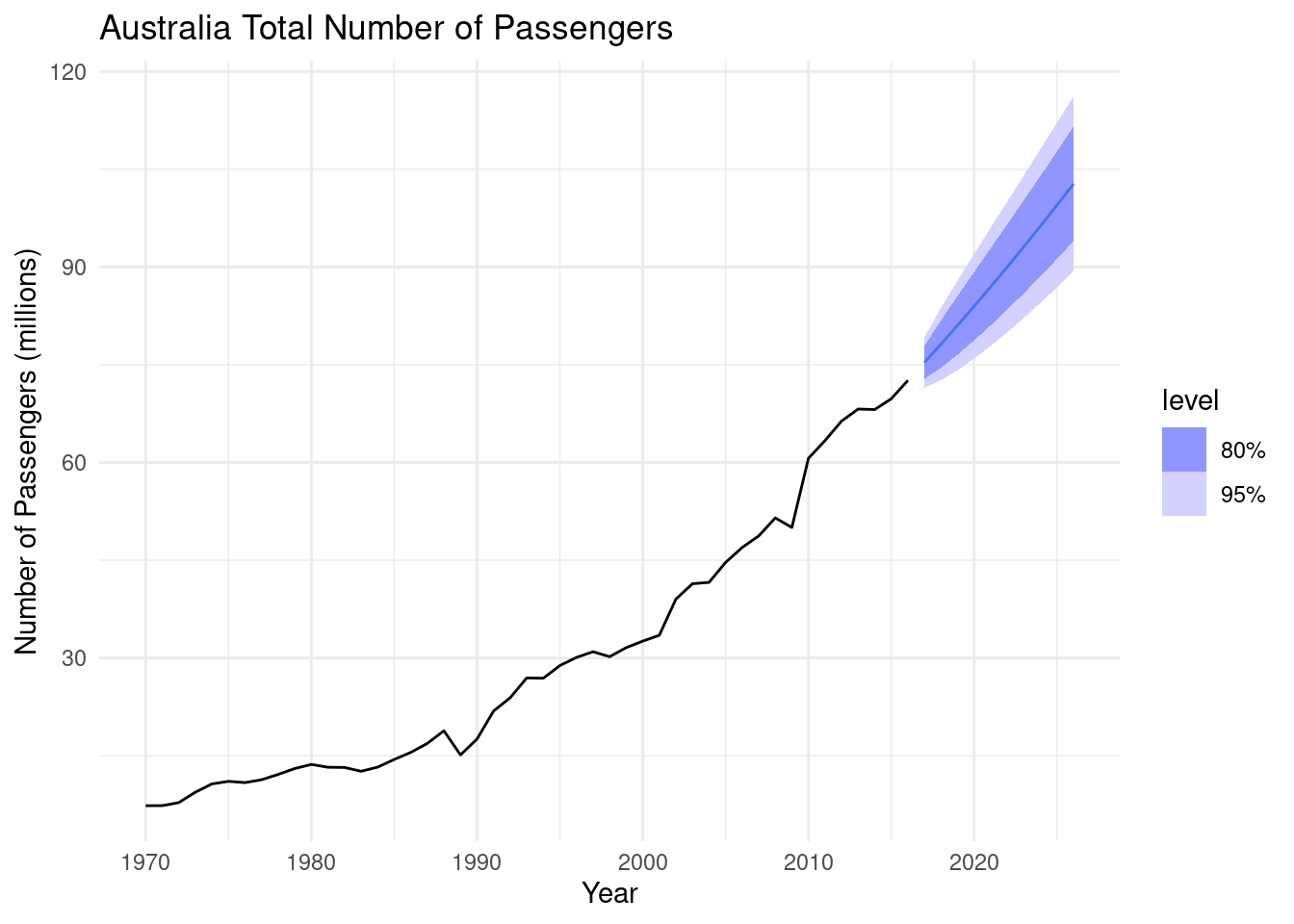
# residuals plots
fit_1 %>% 
  gg_tsresiduals()

# forecasts for the next 10 years (periods)
fit_1 |> forecast(h=10) |>
  autoplot(aus_airpassengers) +
  labs(y = "Number of Passengers (millions)", 
       title = "Australia Total Number of Passengers")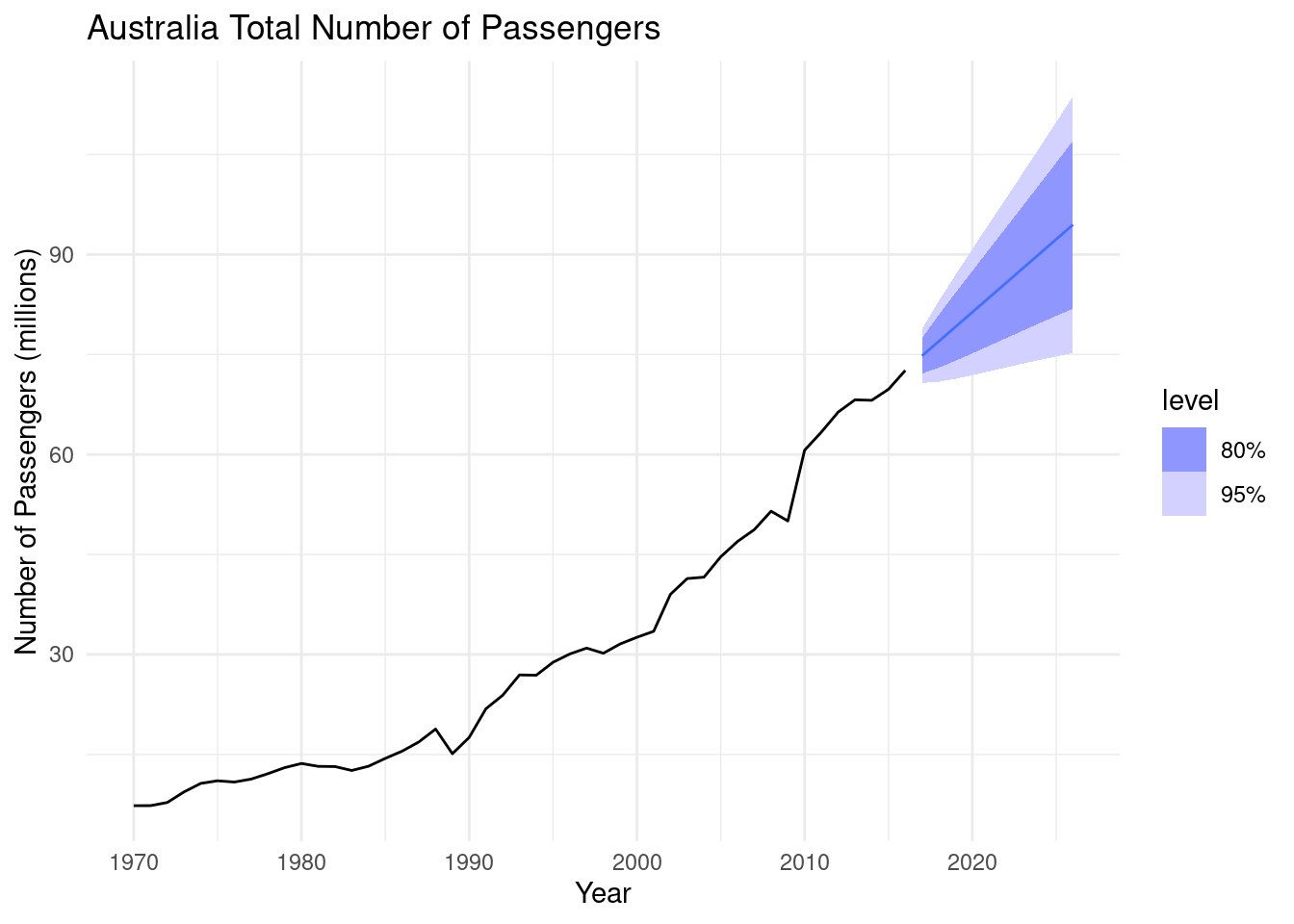

9.1.2 b. Write the model in terms of the backshift operator.

9.1.3 c. Plot forecasts from an ARIMA(0,1,0) model with drift and compare these to part a.

fit_2 <- aus_airpassengers |> 
  model(ARIMA(Passengers ~ 1 + pdq(0, 1, 0)))

report(fit_2)
## Series: Passengers 
## Model: ARIMA(0,1,0) w/ drift 
## 
## Coefficients:
##       constant
##         1.4191
## s.e.    0.3014
## 
## sigma^2 estimated as 4.271:  log likelihood=-98.16
## AIC=200.31   AICc=200.59   BIC=203.97
tidy(fit_2)
## # A tibble: 1 × 6
##   .model                              term  estimate std.error statistic p.value
##   <chr>                               <chr>    <dbl>     <dbl>     <dbl>   <dbl>
## 1 ARIMA(Passengers ~ 1 + pdq(0, 1, 0… cons…     1.42     0.301      4.71 2.32e-5
# plot forecasts (h = 10)
fit_2 |> forecast(h=10) |>
  autoplot(aus_airpassengers) +
  labs(y = "Number of Passengers (millions)", 
       title = "Australia Total Number of Passengers")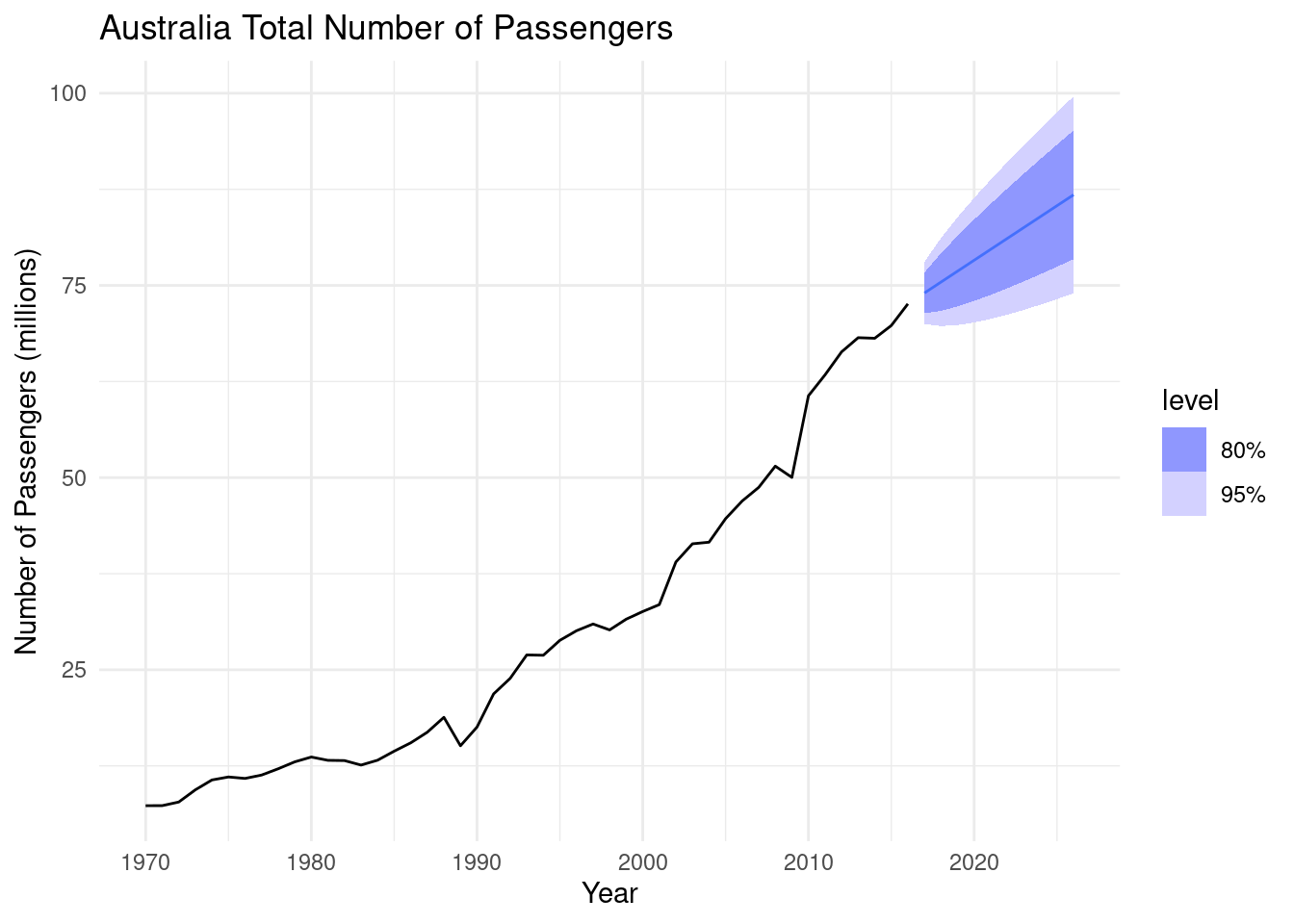

9.1.4 d. Plot forecasts from an ARIMA(2,1,2) model with drift and compare these to parts a. and c.

Remove the constant and see what happens.

fit_3 <- aus_airpassengers |> 
  model(ARIMA(Passengers ~ 1 + pdq(2, 1, 2)))

report(fit_3)
## Series: Passengers 
## Model: ARIMA(2,1,2) w/ drift 
## 
## Coefficients:
##           ar1      ar2     ma1     ma2  constant
##       -0.5518  -0.7327  0.5895  1.0000    3.2216
## s.e.   0.1684   0.1224  0.0916  0.1008    0.7224
## 
## sigma^2 estimated as 4.031:  log likelihood=-96.23
## AIC=204.46   AICc=206.61   BIC=215.43
tidy(fit_3)
## # A tibble: 5 × 6
##   .model                             term  estimate std.error statistic  p.value
##   <chr>                              <chr>    <dbl>     <dbl>     <dbl>    <dbl>
## 1 ARIMA(Passengers ~ 1 + pdq(2, 1, … ar1     -0.552    0.168      -3.28 2.00e- 3
## 2 ARIMA(Passengers ~ 1 + pdq(2, 1, … ar2     -0.733    0.122      -5.99 3.03e- 7
## 3 ARIMA(Passengers ~ 1 + pdq(2, 1, … ma1      0.589    0.0916      6.43 6.45e- 8
## 4 ARIMA(Passengers ~ 1 + pdq(2, 1, … ma2      1.00     0.101       9.92 5.18e-13
## 5 ARIMA(Passengers ~ 1 + pdq(2, 1, … cons…    3.22     0.722       4.46 5.26e- 5
# plot forecasts (h = 10)
fit_3 |> forecast(h=10) |>
  autoplot(aus_airpassengers) +
  labs(y = "Number of Passengers (millions)", 
       title = "Australia Total Number of Passengers")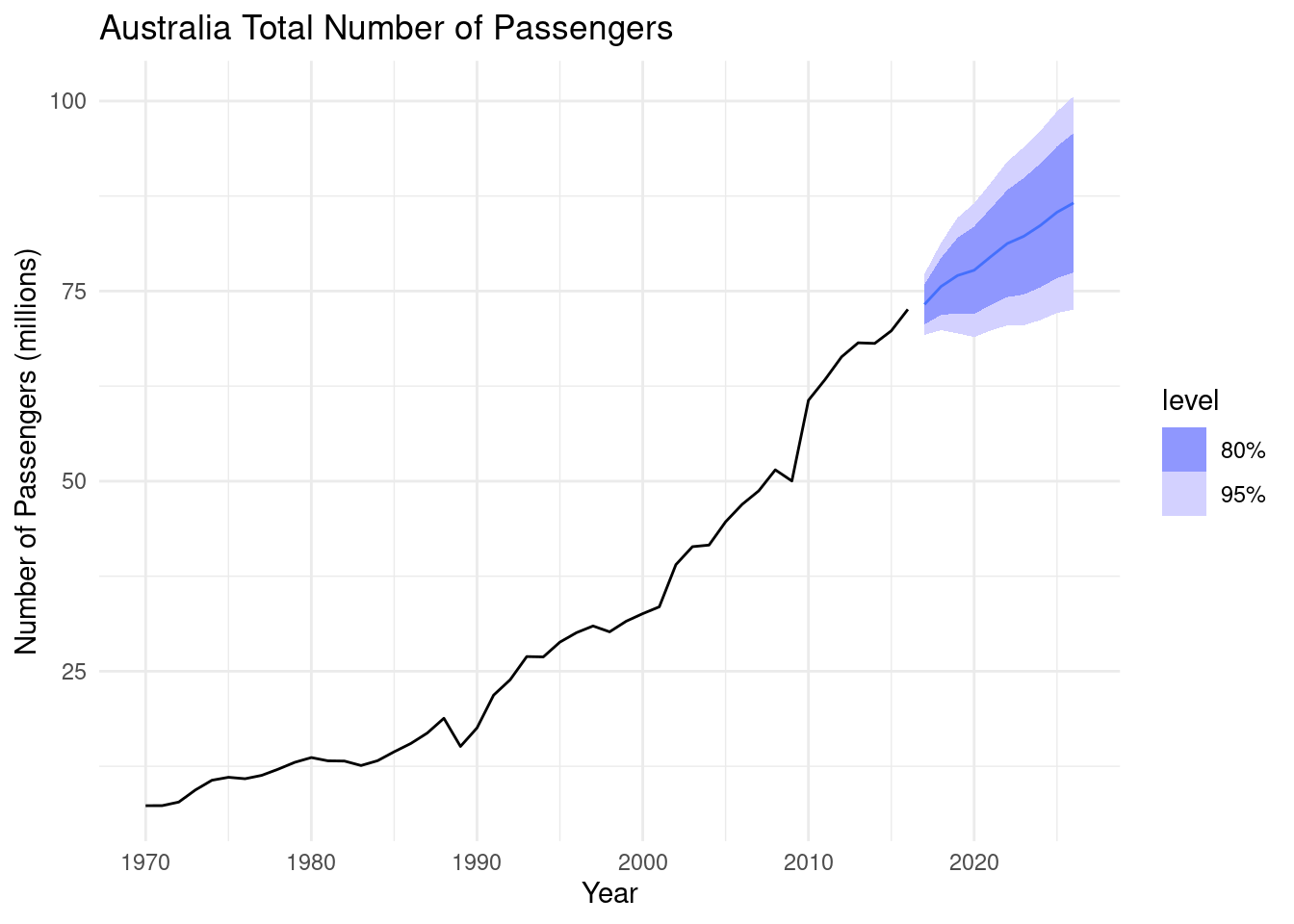

# Arima without constant
fit_3_constant <- aus_airpassengers %>% 
  as.ts() %>% 
  forecast::Arima(c(2, 1, 2), include.constant = TRUE)

fit_3_constant
## Series: . 
## ARIMA(2,1,2) with drift 
## 
## Coefficients:
##           ar1      ar2     ma1     ma2   drift
##       -0.5518  -0.7327  0.5895  1.0000  1.4101
## s.e.   0.1684   0.1224  0.0916  0.1008  0.3162
## 
## sigma^2 = 4.031:  log likelihood = -96.23
## AIC=204.46   AICc=206.61   BIC=215.43
# auto.arima
aus_airpassengers %>% 
  as.ts() %>% 
  forecast::auto.arima()
## Series: . 
## ARIMA(0,2,1) 
## 
## Coefficients:
##           ma1
##       -0.8963
## s.e.   0.0594
## 
## sigma^2 = 4.308:  log likelihood = -97.02
## AIC=198.04   AICc=198.32   BIC=201.65

9.1.5 e. Plot forecasts from an ARIMA(0,2,1) model with a constant. What happens?

fit_4 <- aus_airpassengers |> 
  model(ARIMA(Passengers ~ 1 + pdq(0, 2, 1)))
## Warning: Model specification induces a quadratic or higher order polynomial trend. 
## This is generally discouraged, consider removing the constant or reducing the number of differences.
report(fit_4)
## Series: Passengers 
## Model: ARIMA(0,2,1) w/ poly 
## 
## Coefficients:
##           ma1  constant
##       -1.0000    0.0571
## s.e.   0.0585    0.0213
## 
## sigma^2 estimated as 3.855:  log likelihood=-95.1
## AIC=196.21   AICc=196.79   BIC=201.63
tidy(fit_4)
## # A tibble: 2 × 6
##   .model                             term  estimate std.error statistic  p.value
##   <chr>                              <chr>    <dbl>     <dbl>     <dbl>    <dbl>
## 1 ARIMA(Passengers ~ 1 + pdq(0, 2, … ma1    -1.00      0.0585    -17.1  2.70e-21
## 2 ARIMA(Passengers ~ 1 + pdq(0, 2, … cons…   0.0571    0.0213      2.68 1.03e- 2
# plot forecasts (h = 10)
fit_4 |> forecast(h=10) |>
  autoplot(aus_airpassengers) +
  labs(y = "Number of Passengers (millions)", 
       title = "Australia Total Number of Passengers")