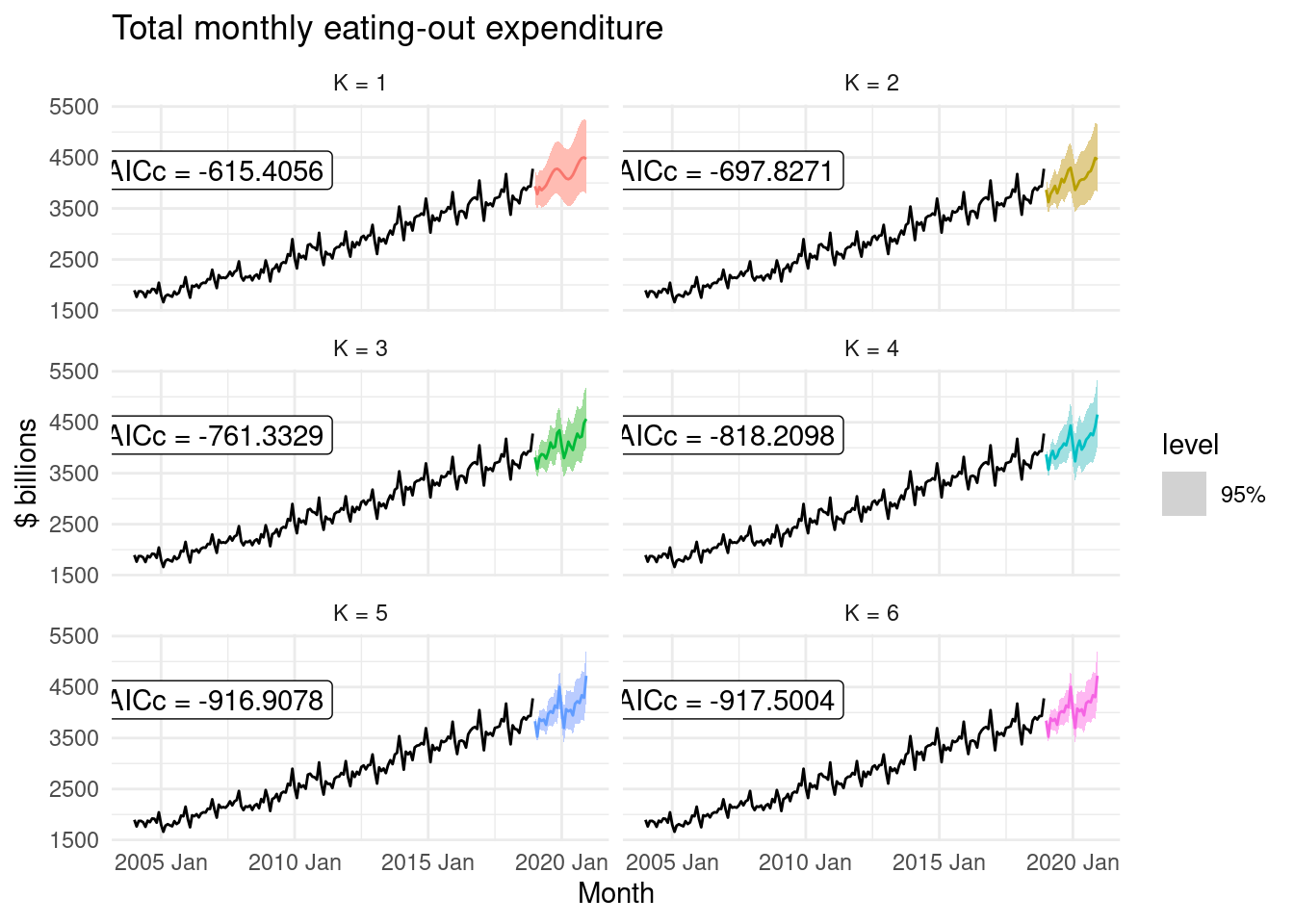
10.6 Dynamics

For long seasonal periods, a dynamic regression with Fourier terms is often better than other models:

aus_cafe <- aus_retail |>
  filter(
    Industry == "Cafes, restaurants and takeaway food services",
    year(Month) %in% 2004:2018
  ) |>
  summarise(Turnover = sum(Turnover))

fit <- model(aus_cafe,
  `K = 1` = ARIMA(log(Turnover) ~ fourier(K=1) + PDQ(0,0,0)),
  `K = 2` = ARIMA(log(Turnover) ~ fourier(K=2) + PDQ(0,0,0)),
  `K = 3` = ARIMA(log(Turnover) ~ fourier(K=3) + PDQ(0,0,0)),
  `K = 4` = ARIMA(log(Turnover) ~ fourier(K=4) + PDQ(0,0,0)),
  `K = 5` = ARIMA(log(Turnover) ~ fourier(K=5) + PDQ(0,0,0)),
  `K = 6` = ARIMA(log(Turnover) ~ fourier(K=6) + PDQ(0,0,0))
)

fit |>
  forecast(h = "2 years") |>
  autoplot(aus_cafe, level = 95) +
  facet_wrap(vars(.model), ncol = 2) +
  guides(colour = "none", fill = "none", level = "none") +
  geom_label(
    aes(x = yearmonth("2007 Jan"), y = 4250,
        label = paste0("AICc = ", format(AICc))),
    data = glance(fit)
  ) +
  labs(title= "Total monthly eating-out expenditure",
       y="$ billions")