Uniform random variables

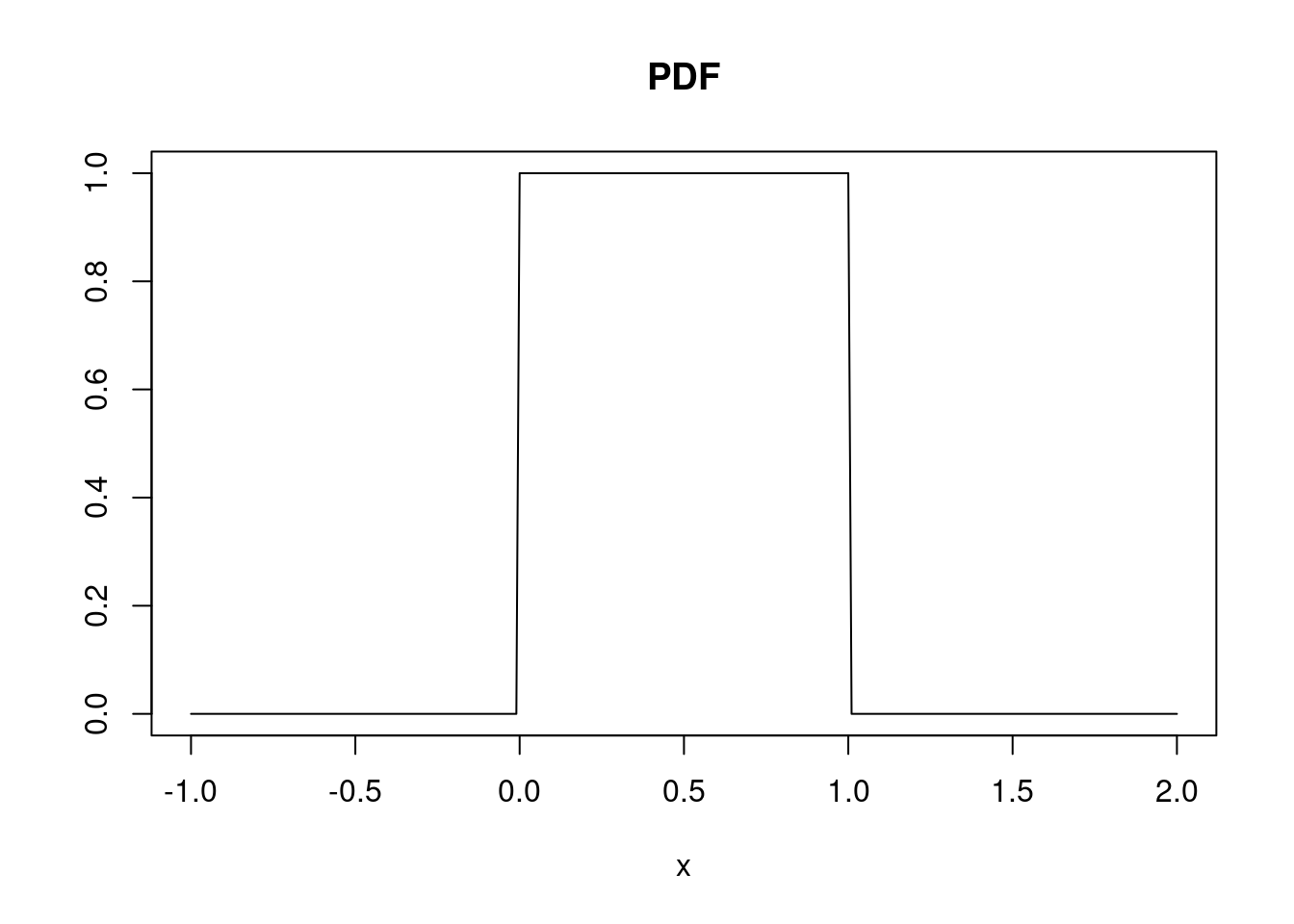
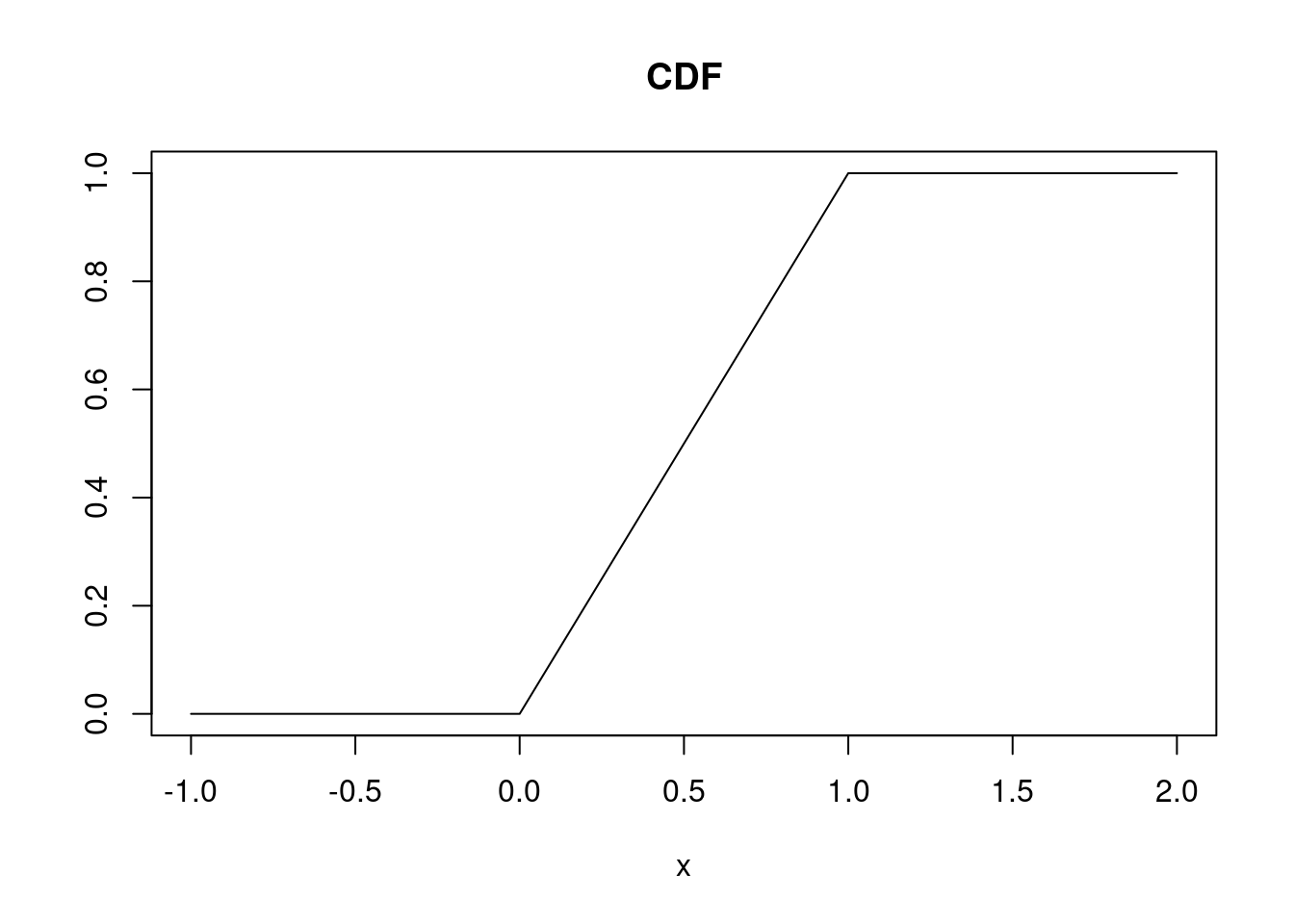
• Definition: Let \(X\) be a continuous uniform random variable defined in an interval \([a; b]\), then:
  • \(f_X(x) = \dfrac{1}{b-a}\), if \(x\in [a; b]\).
  • \(f_X(x) = 0\), if \(x\notin [a; b]\).
  • Notation: \(X \sim Uniform(a, b)\)
• Theorem: If \(X \sim Uniform(a, b)\), then:
  • \(\mathbb{E}[X] = \dfrac{a+b}{2}\).
  • \(Var[X] = \dfrac{(b-a)^2}{12}\).

# Uniform(0, 1)
x <- seq(-1, 2, 0.01)

plot(
  x, dunif(x, 0, 1), type = 'l',
  main = "PDF", xlab = "x", ylab = ""
)

plot(
  x, punif(x, 0, 1), type = 'l',
  main = "CDF", xlab = "x", ylab = "",
  ylim = c(0,1)
)