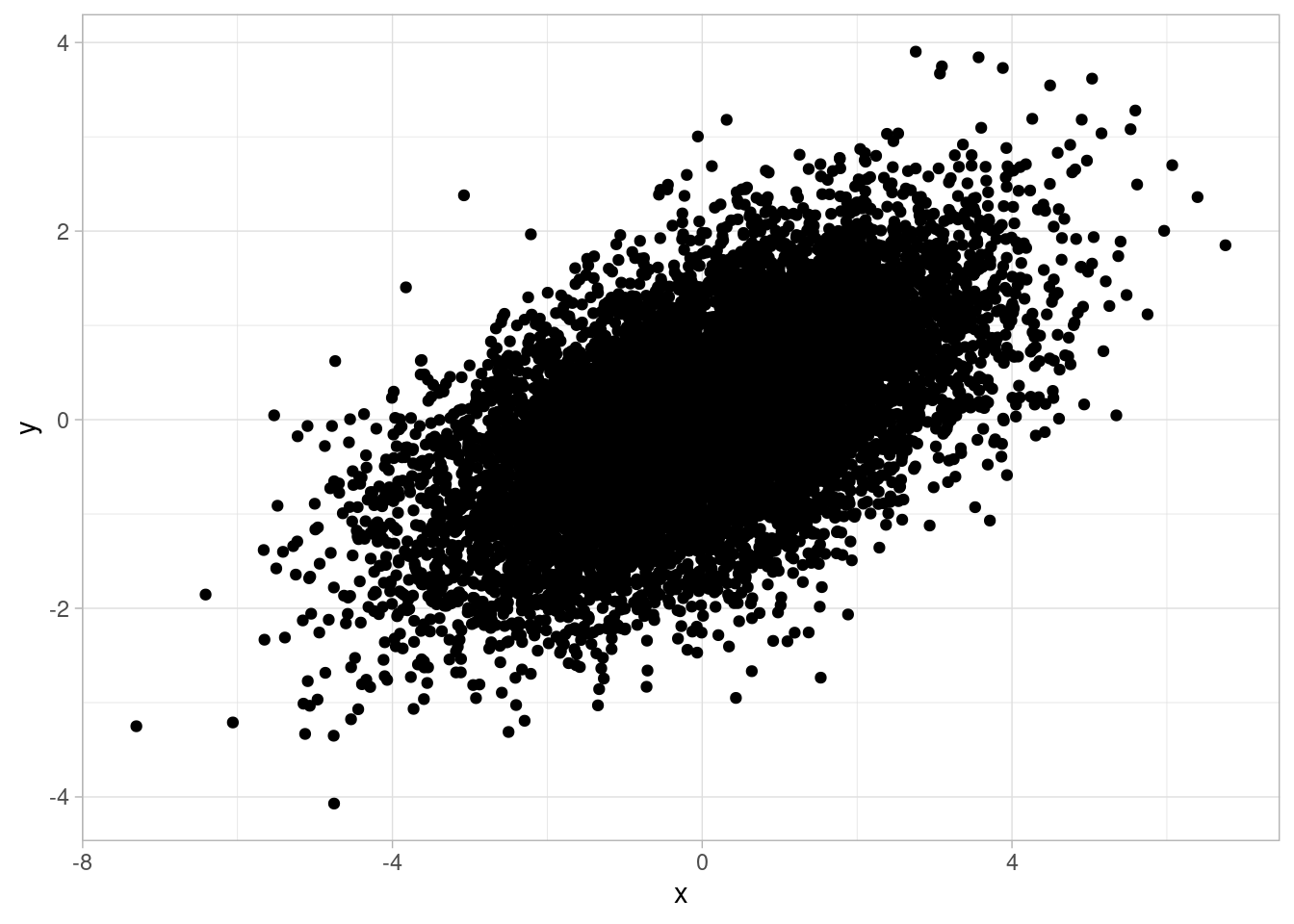
Multidimensional gaussians

An important case of a random vector is the multidimensional Gaussian. For d-dimensions:

$$f_{\mathbf{X}}(\mathbf{x}) = \frac{1}{\sqrt{(2\pi)^d|\mathbf{\Sigma}|}}exp\left( -\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^T\Sigma^{-1}(\mathbf{x}-\mathbf{\mu})\right)$$ It can be shown that:

$$\mathbb{E}[\mathbf{X}] = \mu \text{ and } Cov(\mathbf{X})=\mathbf{\Sigma}$$

If the variables are independant this simplifies (as shown in text):

$$f_{\mathbf{X}}(\mathbf{x}) = \prod_{i=1}^n\frac{1}{\sqrt{(2 \pi)\sigma_i^2}}exp\left(-\frac{(x-\mu_i)^2}{2 \sigma_i^2} \right)$$

where $\sigma_i^2 = Var[X_i]$

Example in R

Recall the example above, where $\Sigma = \begin{bmatrix} 3 & 1 \\ 1 & 1 \end{bmatrix}$

data |> ggplot(aes(x=x,y=y))+geom_point()

Let’s compute the covariance matrix from the data:

cov(data)

##          x        y
## x 3.066814 1.012193
## y 1.012193 1.011582