3.3 Cummulative Distribution Functions (Discrete)

• A cummulative distribution function (CDF) is esentially the cummulative sum of a PMF, from $-\infty$, up to a certain value.

• Definition: Let $X$ be a discrete random variable. The CDF of X is $F_X (x) = \mathcal{P}[X\leq x]$

• Example:

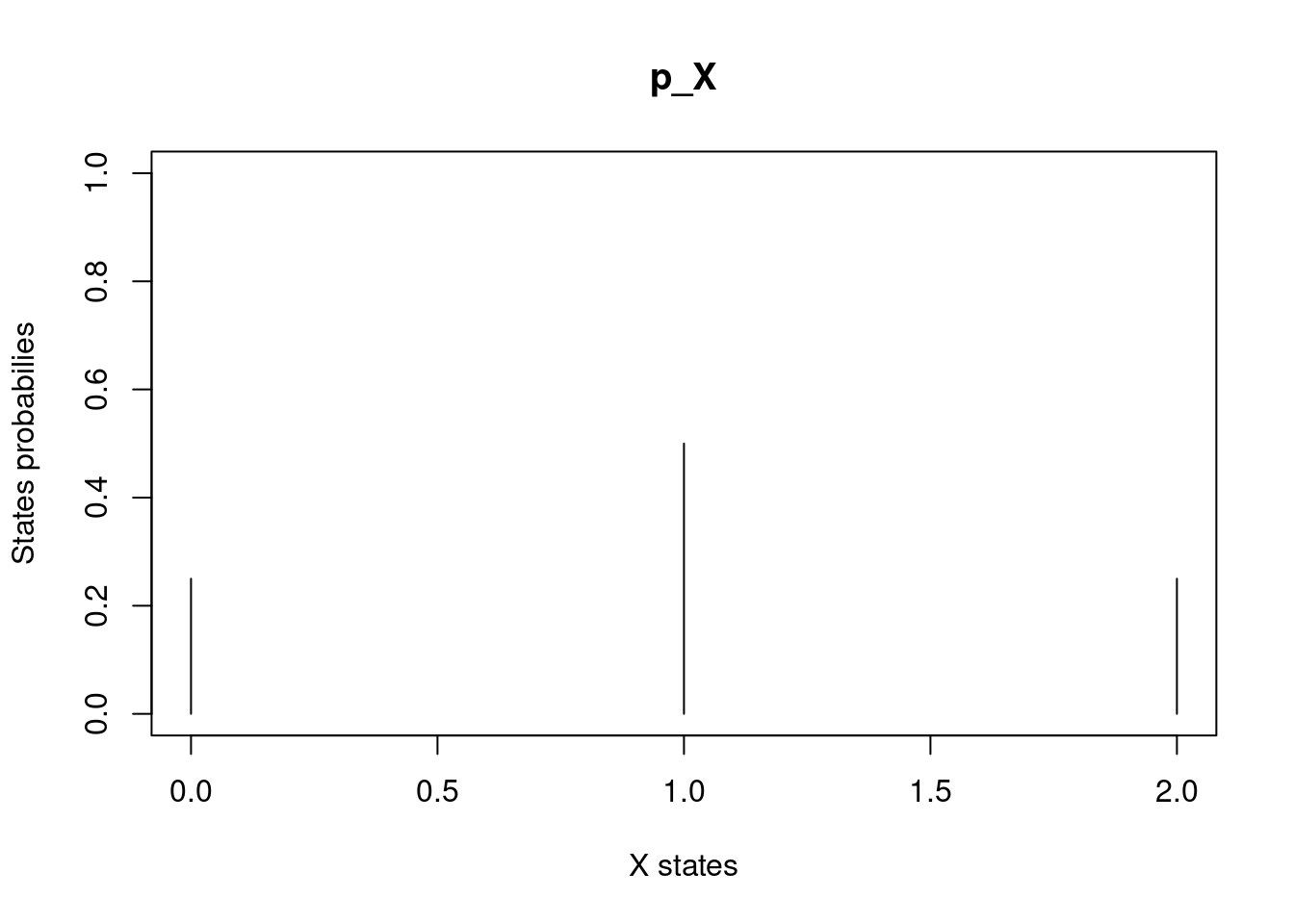
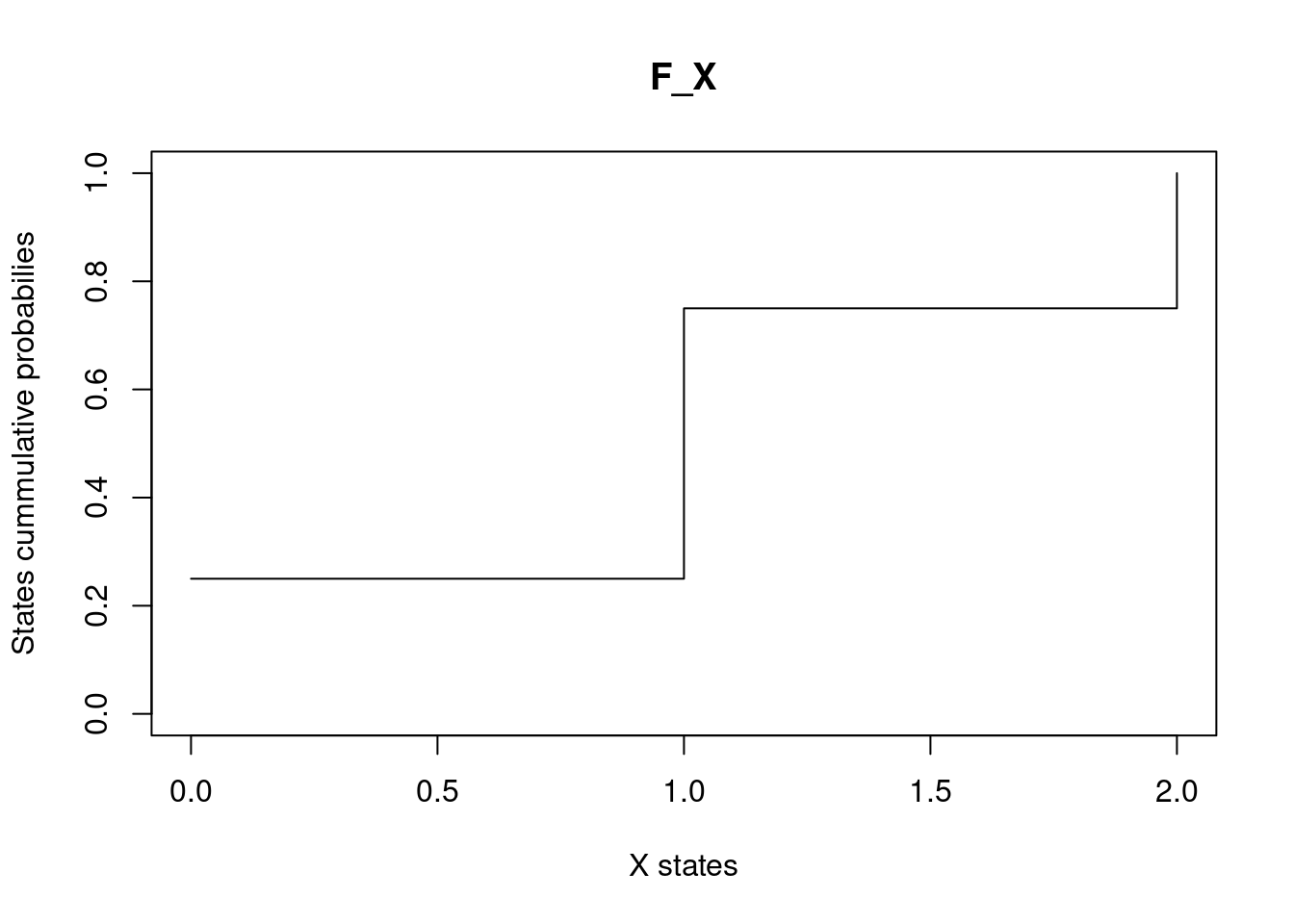
Let $X$ be a random variable with PMF $p_X(0) = 1/4, p_X(1) = 1/2, p_X(2) = 1/4$, then, its CDF is:

$F_X(0) = \mathcal{P}(X\leq 0) = p_X (0) = 1/4$
$F_X(1) = \mathcal{P}(X\leq 1) = p_X (0) + p_X (1) = 3/4$
$F_X(2) = \mathcal{P}(X\leq 2) = p_X (0) + p_X (1) + p_X (2) = 1$

states <- c(0, 1, 2)
probs <- c(1/4, 1/2, 1/4) 
plot(
  states, probs, type = 'h', 
  ylim = c(0,1), main = "p_X",
  xlab = "X states", ylab = "States probabilies"
) 

plot(
  states, cumsum(probs), type = 's',
  ylim = c(0,1), main = "F_X",
  xlab = "X states", ylab = "States cummulative probabilies"
)

• There are technical reasons for why CDFs are easier to work with than PMFs, but, an important one is that the CDF allows us to use mathematical integration.