Independance

Two events are independant if $\mathbb{P}[A \mid B] = \mathbb{P}[A]$ or $\mathbb{P}[B \mid A] = \mathbb{P}[B]$.

Using the definition of conditional probability, if $\mathbb{P}[A] \geq 0$ and $\mathbb{P}[B] \geq 0$ this is: $$\frac{\mathbb{P}[A \cap B]}{\mathbb{P}[B]} = \mathbb{P}[A]\\ \text{or}\\ \mathbb{P}[A \cap B] =\mathbb{P}[B] \mathbb{P}[A]$$ This last expression is often taken as the definition of independent events because it works when probabilities are zero as well. So probabilities for independent events can be multiplied.

Example: outcome of two dice rolls: $A=\{\text{1st die is 3}\}$ and $B= \{\text{2nd die is 4}\}$ .

$\mathbb{P}[A] =\mathbb{P}[B] = 1/6$

$\mathbb{P}[A \cap B] = \mathbb{P}[(3,4)] = 1/36 = \mathbb{P}[A]\mathbb{P}[B]$

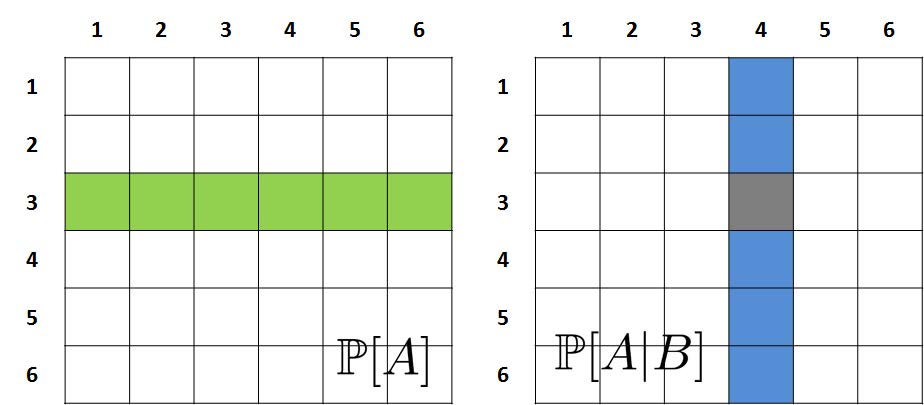
Disjoint is not the same as Independant!