Correlation and independance
- The Correlation coefficient is defined as:
\[ \rho = \frac{Cov(X,Y)}{\sqrt{Var[X]Var[Y]}} \]
- If X and Y are independent, then the book proves they are uncorrelated:
\[ Cov(X,Y) = 0 \\ \text{and so} \\ \mathbb{E}[XY] = \mathbb{E}[X]\mathbb{E}[Y] \]
Note that this is “one way door”: Covariance can be zero for dependent variables.
Computing from data:
\[ \hat{\rho} = \frac{\frac{1}{N}\sum_{n=1}^N x_n y_n - \bar{x}\bar{y}}{\sqrt{\frac{1}{N}\sum_{n=1}^N(x_n-\bar{x})^2}\sqrt{\frac{1}{N}\sum_{n=1}^N(y_n-\bar{y})^2}} \]
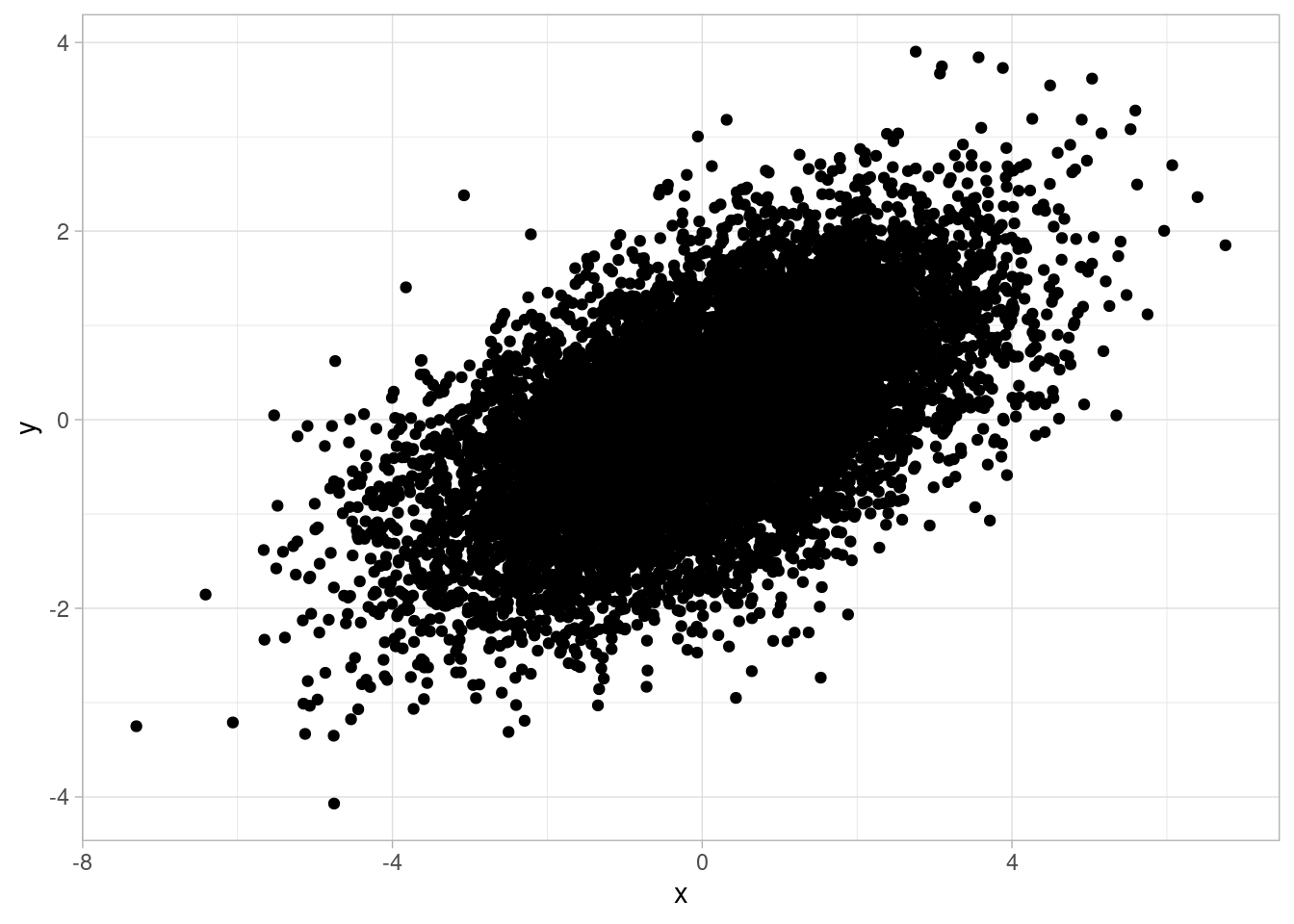
sigma <- matrix(c(3,1,1,1),nrow=2)
m <- mvrnorm(n=10000, mu=c(0,0), Sigma = sigma)
data <- tibble(x = m[,1], y=m[,2])
print(cor(data$x,data$y))## [1] 0.5746705## [1] 0.5773503