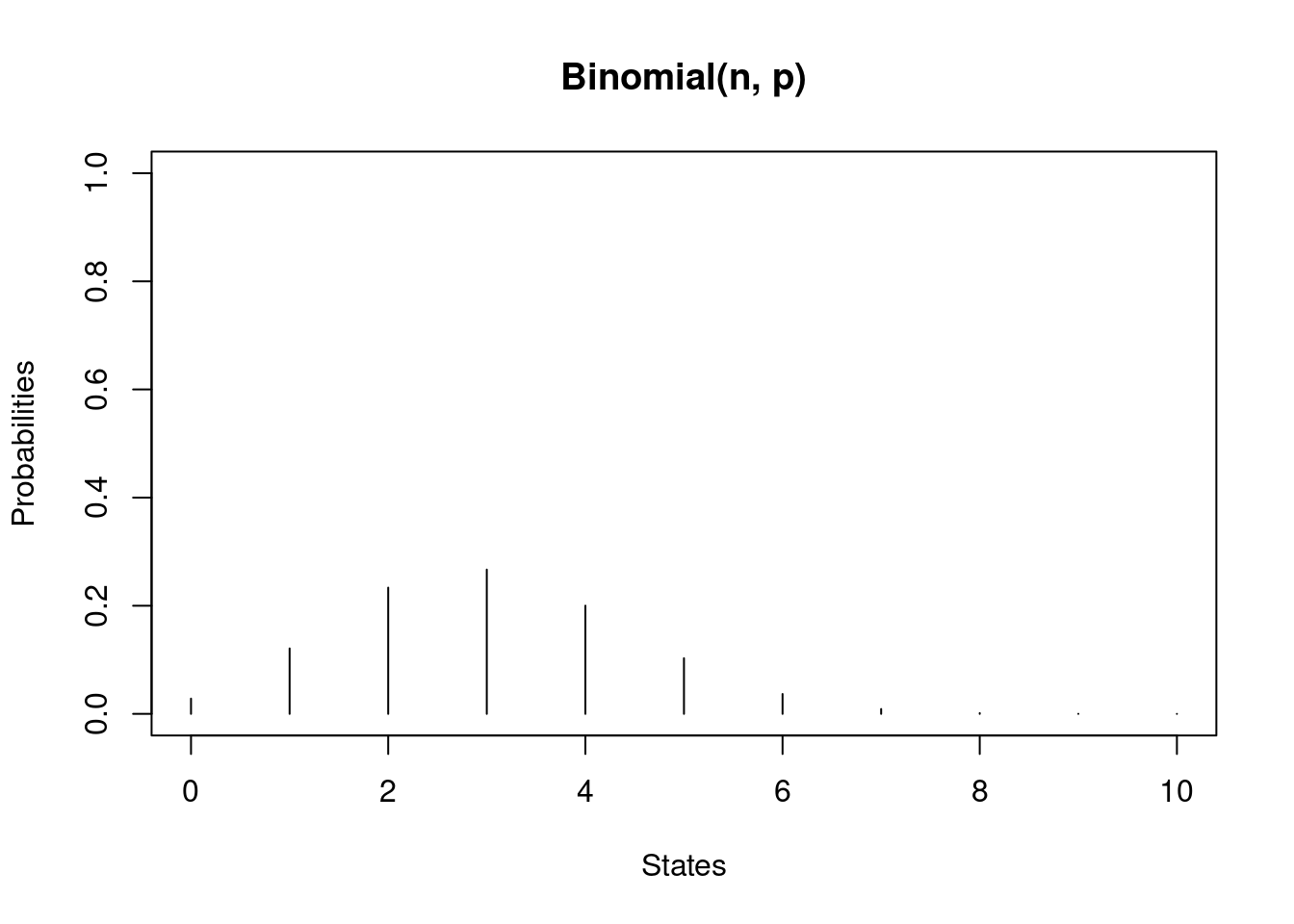
Binomial random variable

• Definition: Let \(X\) be a binomial random variable, then:

  • \(p_X(k) = {n \choose k}p^k (1-p)^{n-k}\), where \(p\) is a fixed value in \((0, 1)\) called the binomial parameter, \(n\) is the total number of states, and \(k\) belongs in \(\left\{ 0, 1, \dots, n \right\}\)

  • Notation: \(X \sim Binomial(n, p)\)

• Theorem: Let \(X \sim Binomial(n, p)\), then:
  • \(\mathbb{E}[X] = np\)
  • \(\mathbb{E}[X^2] = np(np + (1-p))\)
  • \(Var[X] = np\cdot (1-p)\)

n <- 10
states <- 0:n
p <- 0.3

plot(
  states, dbinom(states, n, p), type = 'h',
  ylim = c(0, 1), main = "Binomial(n, p)",
  xlab = "States", ylab = "Probabilities"
)