Disjoint and Partition

• Two sets \(A\) and \(B\) are disjoint if \(A\cap B = \emptyset\)

• A collection of sets \(\{A_1,A_2,...,A_n\}\) is a partition of \(\Omega\) if:

  1. Disjoint: \(A_i \cap A_j = \emptyset\)
  2. Decompose: \(\bigcup_{i=1}^n A_i = \Omega\)

• This is important because it allows us to decompose \(\Omega\) into smaller subsets to analyze separately.

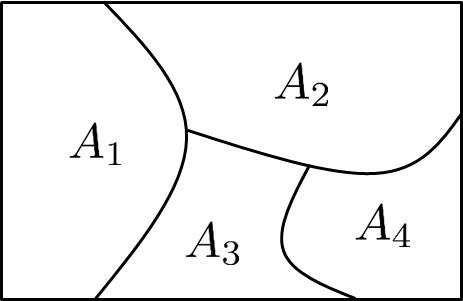
Example \(\{1,3,4\}\), \(\{4,5\}\) and \(\{6\}\) form a partition of \(\{1,2,3,4,5,6\}\)