Exponential random variables

• Definition: Let $X$ be an exponential random variable with parameter $\lambda > 0$, then:
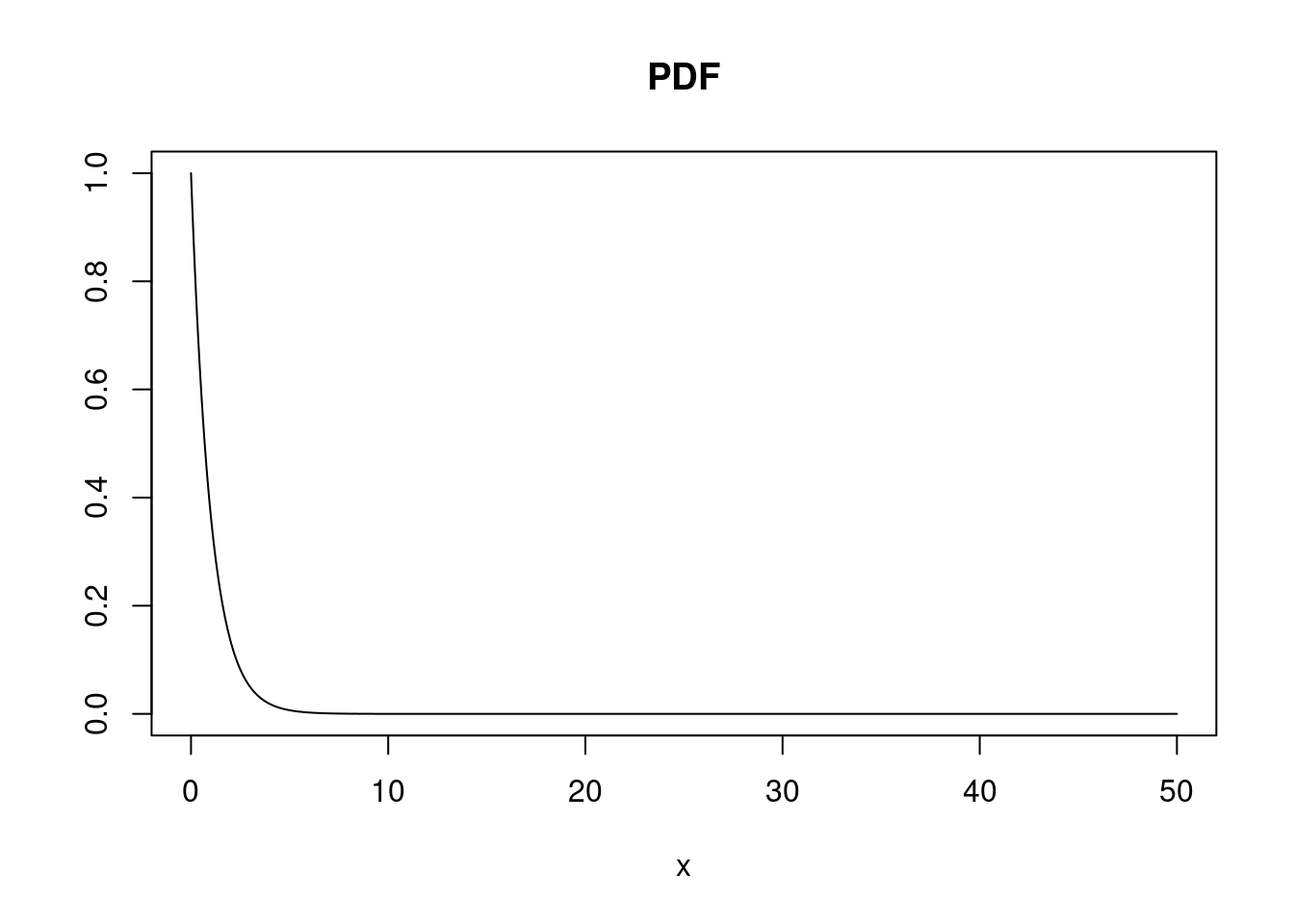
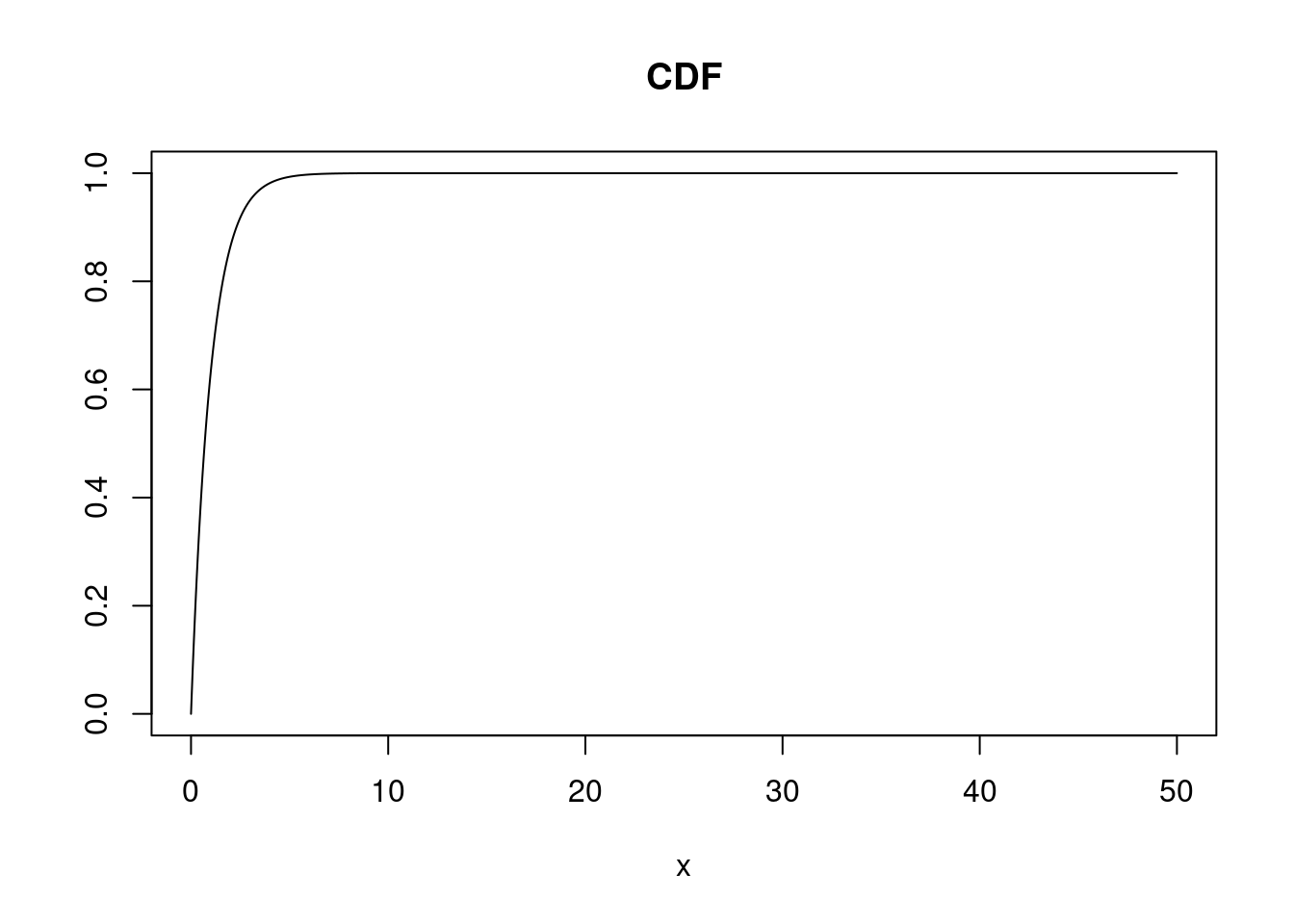
  • $f_X(x) = \lambda e^{-\lambda x}$, if $x\geq 0$.
  • $f_X(x) = 0$, if $x<0$.
  • $\lambda$ stands for the rate of decay … larger $\lambda$, faster decay.
  • Notation: $X \sim Exponential(\lambda)$
• Theorem: If $X \sim Exponential(\lambda)$, then:
  • $\mathbb{E}[X] = \dfrac{1}{\lambda}$.
  • $Var[X] = \dfrac{1}{\lambda^2}$.
• Remember that a Poisson random variable describes the number of events that happend in a certain period. Then, an exponential variable is the interarrival time between two consecutive Poisson events; that is, how much time it takes to fo from $N$ Poisson counts to $N+1$ Poisson counts.

# Exponential(lambda = 1)
x <- seq(0, 50, 0.01)
lambda <- 1

plot(
  x, dexp(x, 1), type = 'l',
  main = "PDF", xlab = "x", ylab = ""
)

plot(
  x, pexp(x, 1), type = 'l',
  main = "CDF", xlab = "x", ylab = "",
  ylim = c(0,1)
)