Transformations of Gaussians

If we transform a random vector of dimension N with a linear transformation \(\mathbf{Y} = \mathbf{A X} + \mathbf{b}\) where \(\mathbf{A}\) is an NxN matrix, the text shows that (not just for Gaussians!):

\[ \mathbf{\mu_Y} = \mathbf{A\mu_X + b}\\ \mathbf{\Sigma_Y}= \mathbf{A\Sigma_XA^T} \]

This shows in general how to rotate and scale random vectors.

Eigendecomposition

The text reviews the concepts of finding the eigenvectors and eigenvalues of matrix. The main result for us is that we can diagonalize the covariance matrix:

\[ \mathbf{\Sigma} = \mathbf{U\Lambda U^T} \]

where \(\Lambda\) is a diagonal matrix with the eigenvalues along the diagonal, and \(\mathbf{U}\) is the matrix formed from the corresponding normalized eigenvectors:

\[ \mathbf{U} = \begin{bmatrix} \mathbf{u}_1 & ... & \mathbf{u}_N \end{bmatrix} \]

The columns are \(U\) are orthonormal (\(U^TU=I\)) and can serve as a basis:

\[ \begin{align} &\mathbf{x} = \sum_{j=1}^N\alpha_j \mathbf{u}_j \\ \\ &\text{with basis coefficients:}\\ \\ &\alpha_j = \mathbf{u}_j^T\mathbf{x} \end{align} \]

This allows us to understand the multivariate Gaussian: the basis vectors are the orientation of the ellipsoids and the eigenvalues are the width of the distribution along those basis vector directions.

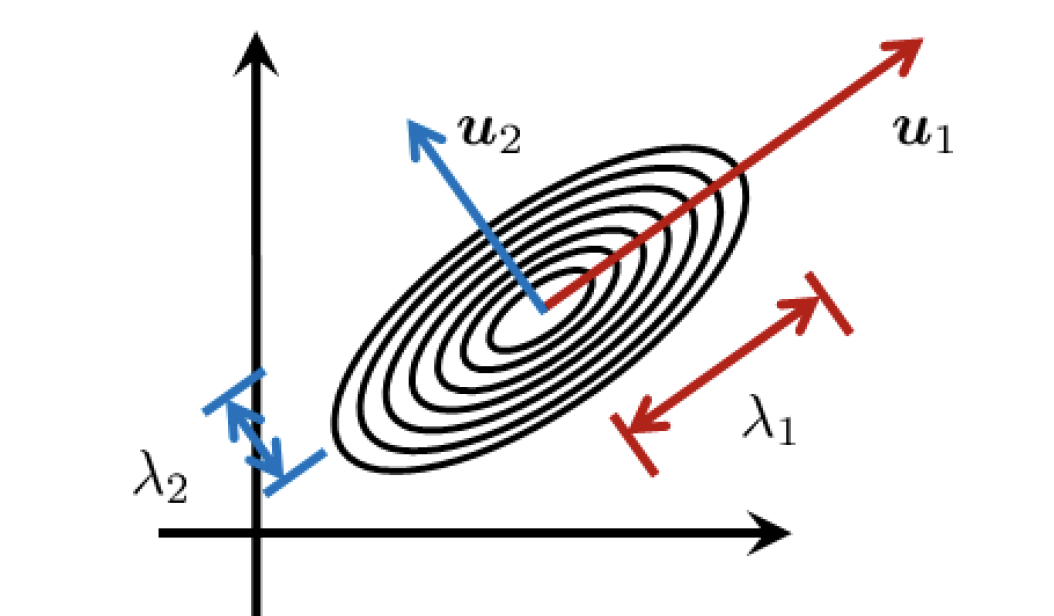
Note: the covariance matrix must be symmetric positive semi-definite, which means it must be symmetric and the eigenvalues cannot be negative. This makes sense when you look at the structure of the covariance matrix!