Standard Gaussian

• The PDF of a gaussian random variable does not have an antiderivative expressable in closed-form (expression that uses a finite amount of standard operations (basic functions and basic arithmetic operations)).

• The common solution is to numerically approximate operations regarding the CDF of Gaussian(0, 1).

• Definition: The standard Gaussian/normal random variable $X\sim N(0,1)$ has a :

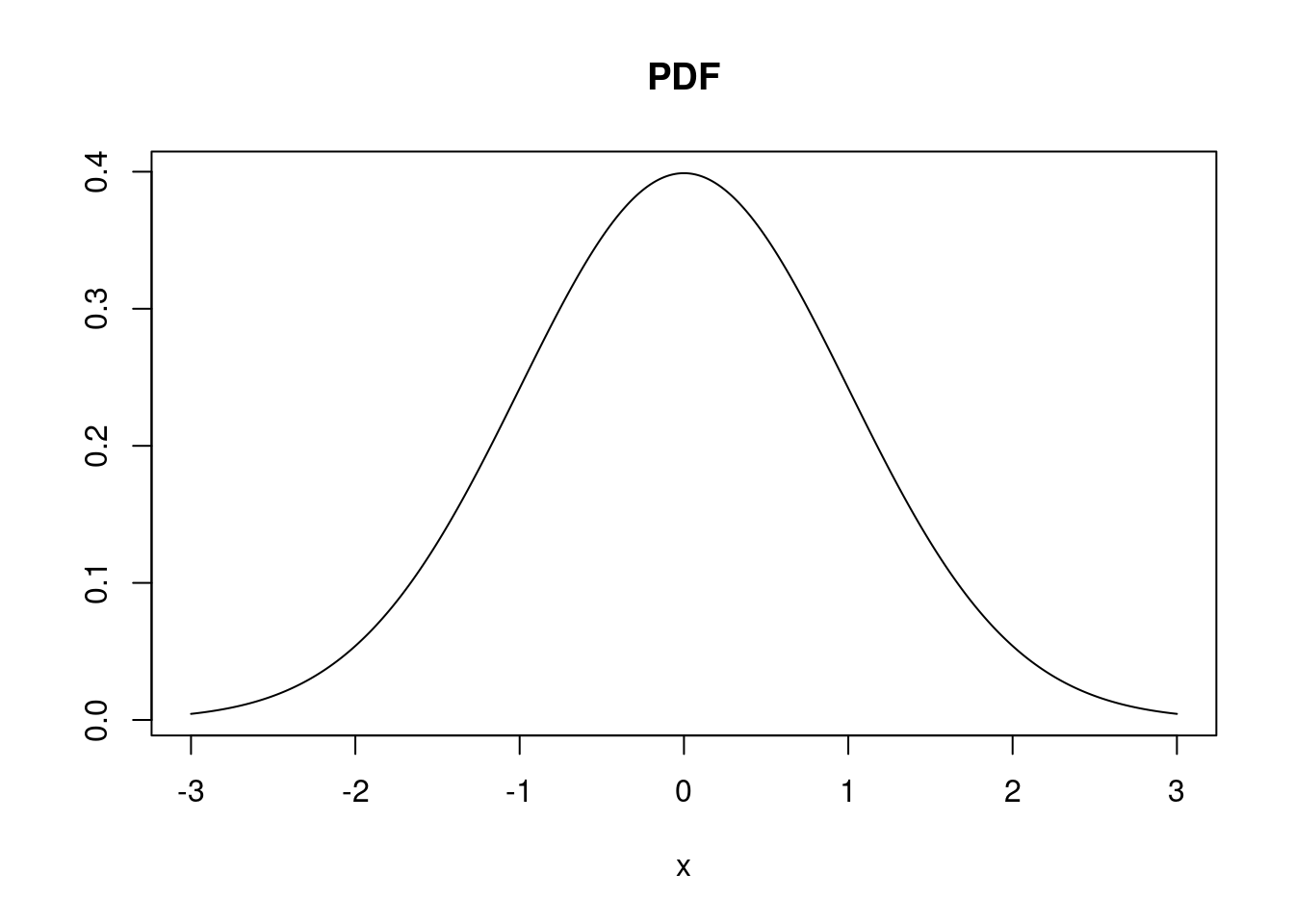
  • PDF: $f_X(x) =\dfrac{1}{\sqrt{2\pi}}e^{-\dfrac{x^2}{2}}$.
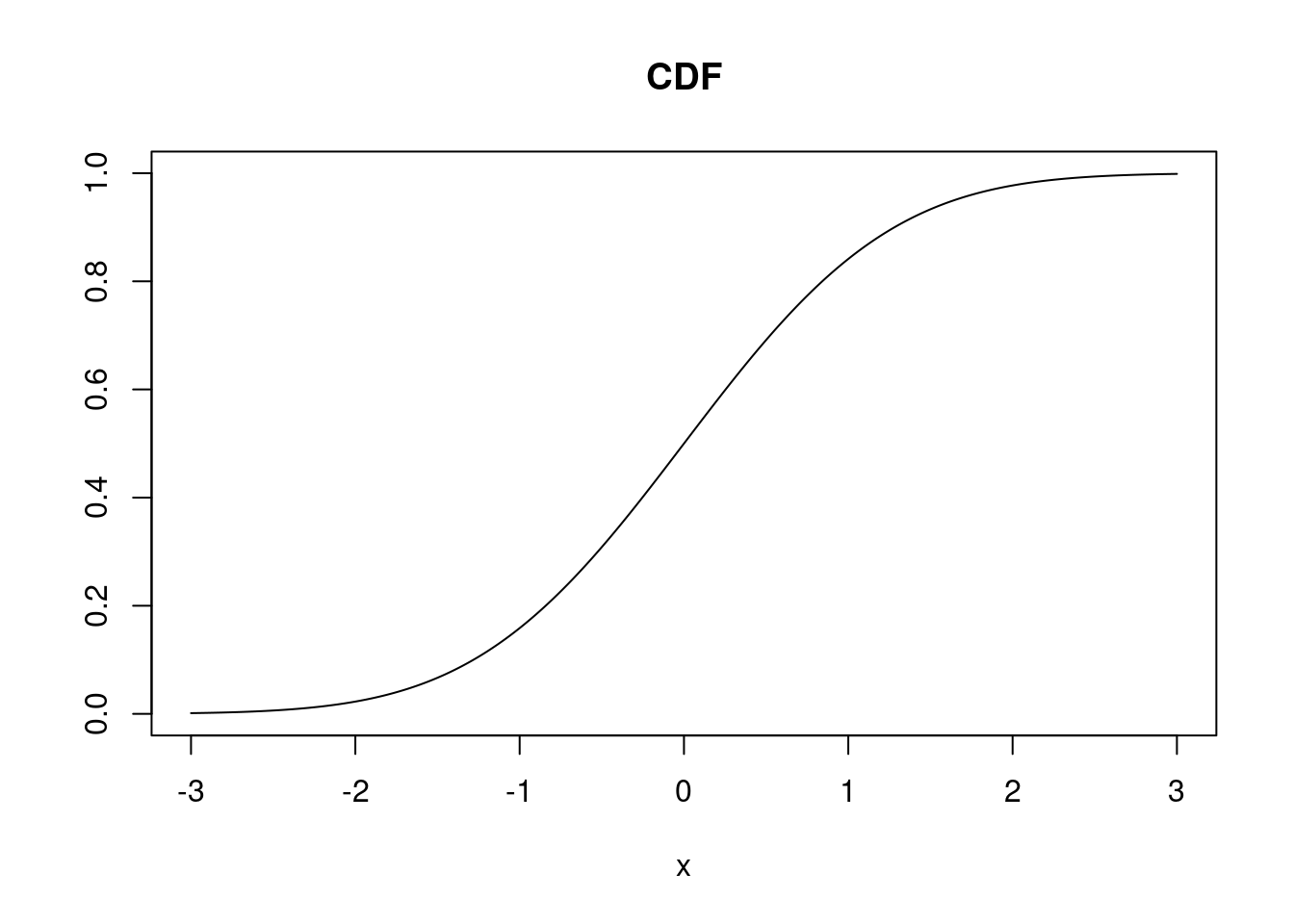
  • CDF: $\Phi(x) = F_X(x) = \dfrac{1}{\sqrt{2\pi}} \displaystyle{ \int\limits_{-\infty}^{x} } e^{-\frac{t^2}{2}}\; dt$

• Theorem: Let $X \sim \mathcal{N}(\mu, \sigma^2)$, then $F_X(x) = \Phi \left( \dfrac{x-\mu}{\sigma} \right)$

# Gaussian(mean = 0, variance = 1)
x <- seq(-3, 3, 0.01)
mean <- 0
standard_deviation <- 1

plot(
  x, dnorm(x, mean, standard_deviation), type = 'l',
  main = "PDF", xlab = "x", ylab = ""
)

plot(
  x, pnorm(x, mean, standard_deviation), type = 'l',
  main = "CDF", xlab = "x", ylab = "",
  ylim = c(0,1)
)