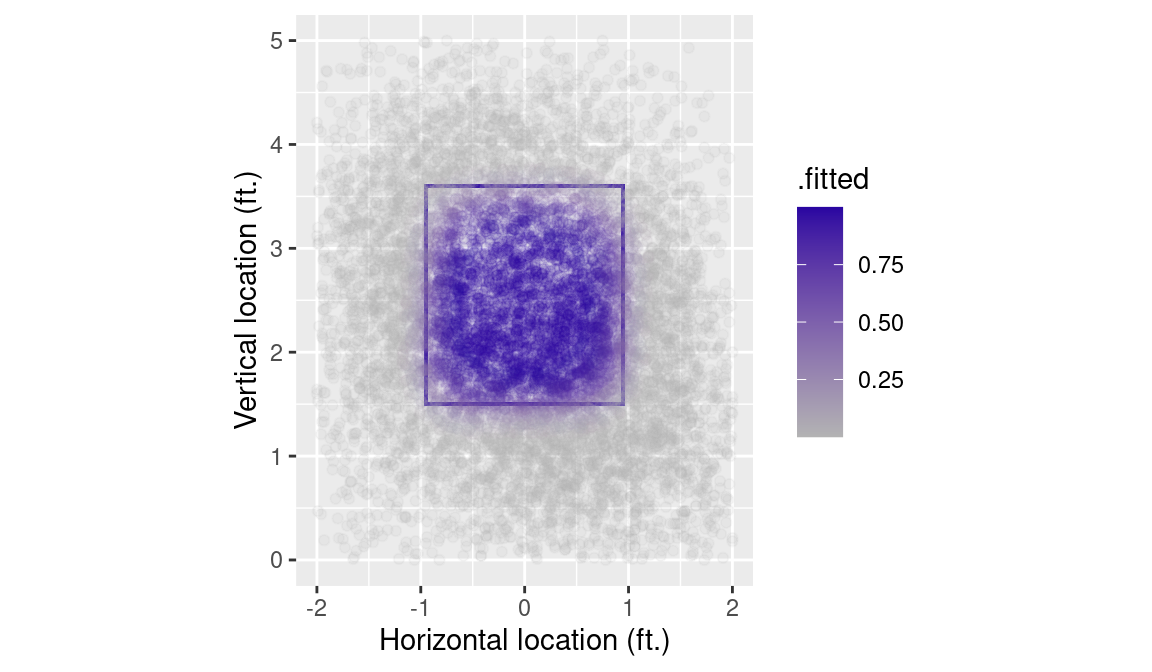
7.5 Modeling Called Strike Percentage

• We use a Generalized Additive Model with binomial family

library(mgcv)
strike_mod <- gam(
  Outcome == "called_strike" ~ s(plate_x, plate_z), 
  family = binomial, 
  data = taken
)

library(broom)
hats <- strike_mod |>
  augment(type.predict = "response")

k_zone_plot %+% sample_n(hats, 10000) +
  geom_point(aes(color = .fitted), alpha = 0.1) + 
  scale_color_gradient(low = "gray70", high = crcblue)

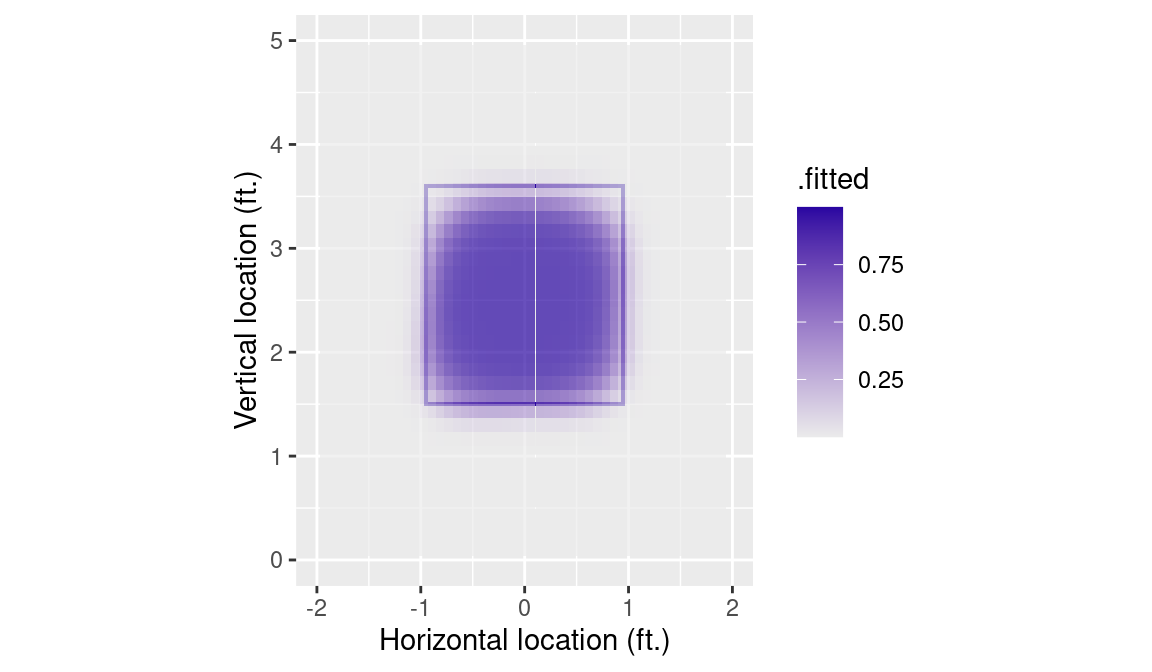
• We can build a continuous grid

library(modelr)
grid <- taken |>
  data_grid(
    plate_x = seq_range(plate_x, n = 100), 
    plate_z = seq_range(plate_z, n = 100)
  )

grid_hats <- strike_mod |>
  augment(type.predict = "response", newdata = grid)

tile_plot <- k_zone_plot %+% grid_hats +
  geom_tile(aes(fill = .fitted), alpha = 0.7) + 
  scale_fill_gradient(low = "gray92", high = crcblue)
tile_plot

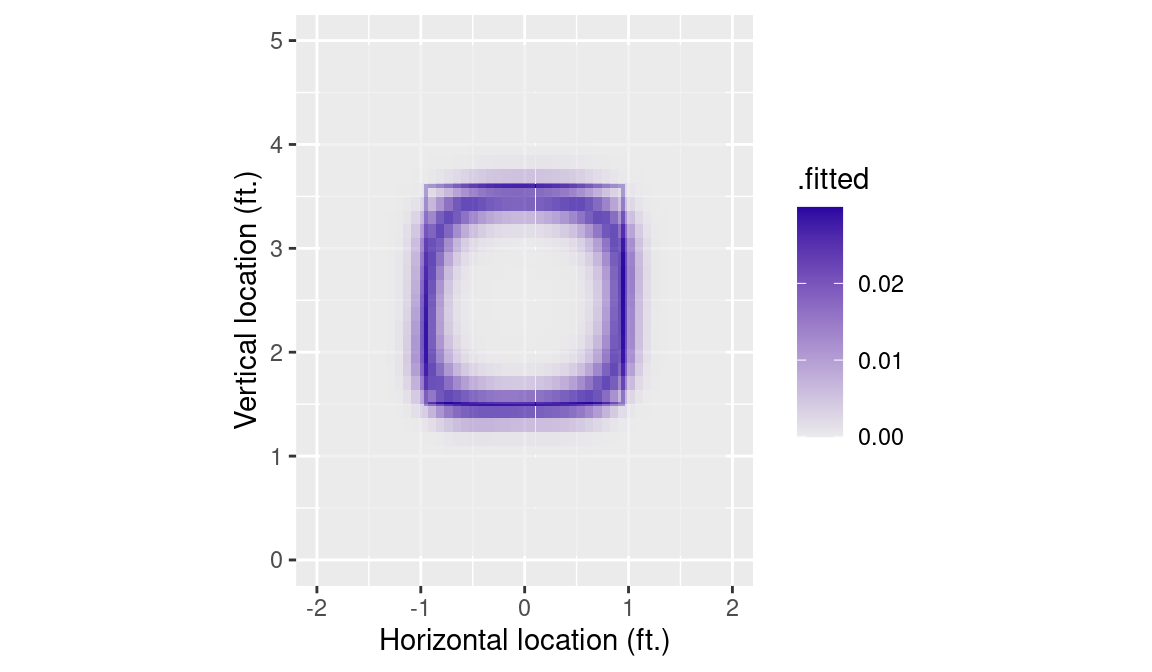
• Batter and pitcher handedness may have an effect, let’s add it to our GAM

hand_mod <- gam(
  Outcome == "called_strike" ~ 
    p_throws + stand + s(plate_x, plate_z), 
  family = binomial, 
  data = taken
)

hand_grid <- taken |>
  data_grid(
    plate_x = seq_range(plate_x, n = 100), 
    plate_z = seq_range(plate_z, n = 100),
    p_throws, 
    stand
  )
hand_grid_hats <- hand_mod |>
  augment(type.predict = "response", newdata = hand_grid)

diffs <- hand_grid_hats |>
  group_by(plate_x, plate_z) |>
  summarize(
    N = n(), 
    .fitted = sd(.fitted),
    .groups = "drop"
  )
tile_plot %+% diffs