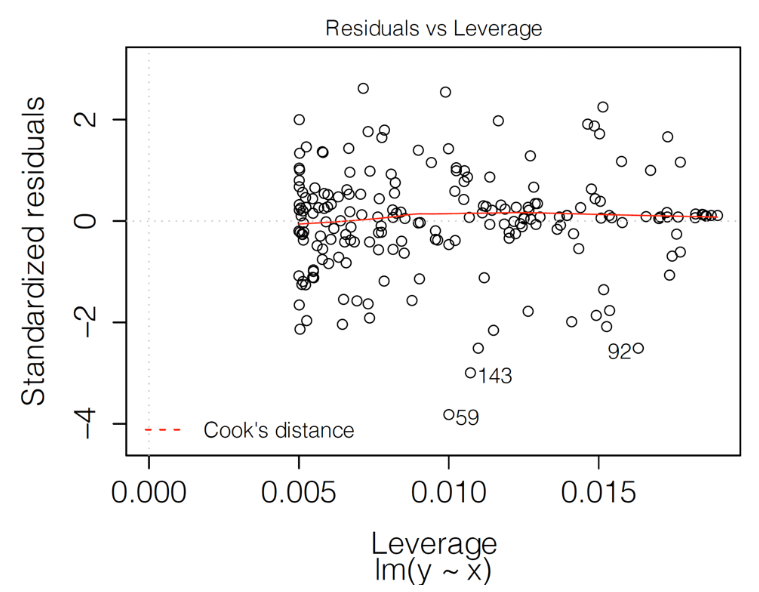
Standardized residuals $\tilde{r}_i$ in function of leverage $l_i$

• Leverage $l_i$ is a measure of how far away the independent variable values of an observation are from those of the other observations.

• Data points with large residuals (outliers) and/or high leverage may distort the outcome and accuracy of a regression.

• The predicted sum-of-squares:

$$\begin{equation} PRESS = \sum_{i=1}^{n} (\widehat{y}_{i(-i)} - y_i)^2 = \sum_{i=1}^{n} \frac{r_i^2}{(1-l_{i})^2} \end{equation}$$

• Cook’s distance measures the effect of deleting a given observation.