Aside on log transformations

Note: This following material was not discussed in the EMA book.

Fitting a regression model on a log transformed target variable, then applying the inverse operation on the logged model prediction will result in biased predictions. This may or may not be a problem depending on your goals, loss functions, etc.

Helpful links:

Refer to the references below regarding techniques for bias correction when logging the target variable:

• Duan’s transformation: https://stats.stackexchange.com/questions/55692/back-transformation-of-an-mlr-model
  
• Example of Duan’s smearing in python: https://andrewpwheeler.com/tag/linear-regression/
• Alternative smearing adjustment using regression without an intercept: https://stats.stackexchange.com/questions/361618/how-to-back-transform-a-log-transformed-regression-model-in-r-with-bias-correcti
  
• Good discussion on target variable transformation: https://florianwilhelm.info/2020/05/honey_i_shrunk_the_target_variable/
  
• Lognormal smearing: https://en.wikipedia.org/wiki/Smearing_retransformation
  
• Forecasting bias: https://arxiv.org/pdf/2208.12264

Example Bias Adjustment factors using Duan’s Transformation

Duan’s transformation Formula using log base 10: \[\hat{Y}_j = 10^{(\widehat{\log_{10}{Y}}_j)} \cdot \frac{1}{N}\sum_{i=1}^N 10^{e_i}\]
where \(\widehat{\log_{10}{Y}}_j\) is the model’s prediction on the logged scale, and \(e_i\) is the model residual on the logged scale (i.e. \(log_{10} Y - \widehat{\log_{10}{Y}}_j\)).

ols smearing adjustment: 1.032

rf smearing adjustment: 1.008

gbm shallow smearing adjustment: 1.049

gbm deep smearing adjustment: 1.02

Below is a comparison of model performance on our test set using three different modeling methodologies:

• Using the raw scale target variable for modeling
• Using the log transformed target for modeling, then taking the inverse
• Using the log transformed target for modeling, then taking the inverse * smearing adjustment

Fig 1: Raw Scale

Fig 2: Back-transformed Log Scale

Fig 3: Back-transformed Log Scale with Smearing

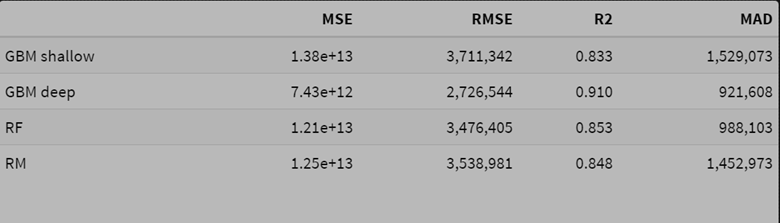
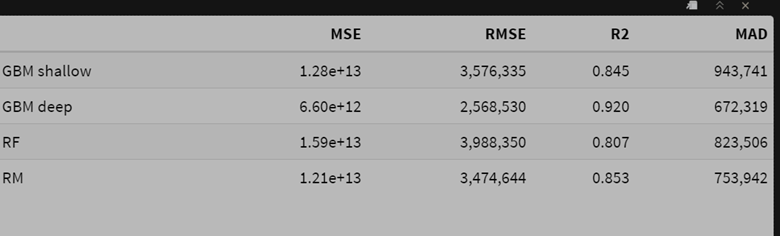
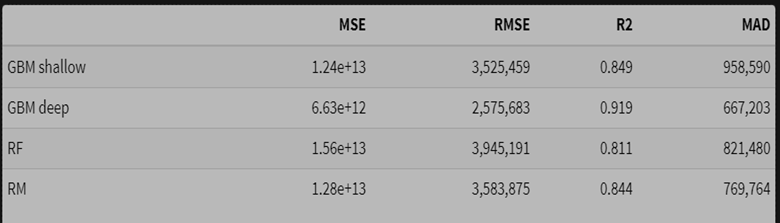
Observations:

• The random forest model performs best in terms of squared error on the raw scale.
• The smearing adjustment improves the random forest compared to the basic back-transformed log model.
  
• The deep GBM model’s MAD value improves slightly with smearing, with a very small deterioration in squared error.