18.4 Parsing and grammar

Parsing - The process by which a computer language takes a string and constructs an expression. Parsing is governed by a set of rules known as a grammar.
We are going to use lobstr::ast() to explore some of the details of R’s grammar, and then show how you can transform back and forth between expressions and strings.
Operator precedence - Conventions used by the programming language to resolve ambiguity.
Infix functions introduce two sources of ambiguity.
The first source of ambiguity arises from infix functions: what does 1 + 2 * 3 yield? Do you get 9 (i.e., (1 + 2) * 3), or 7 (i.e., 1 + (2 * 3))? In other words, which of the two possible parse trees below does R use?

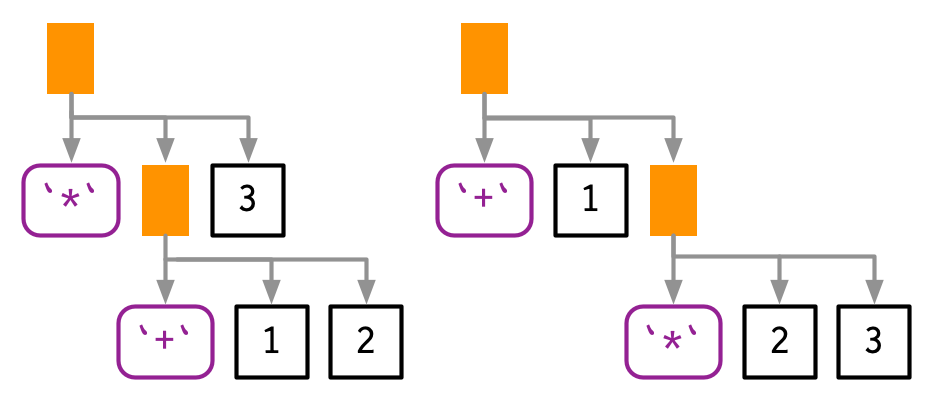
Programming languages use conventions called operator precedence to resolve this ambiguity. We can use ast() to see what R does:

lobstr::ast(1 + 2 * 3)
#> █─`+` 
#> ├─1 
#> └─█─`*` 
#>   ├─2 
#>   └─3

PEMDAS (or BEDMAS or BODMAS, depending on where in the world you grew up) is pretty clear on what to do. Other operator precedence isn’t as clear.
There’s one particularly surprising case in R:
- ! has a much lower precedence (i.e., it binds less tightly) than you might expect.
- This allows you to write useful operations like:

lobstr::ast(!x %in% y)
#> █─`!` 
#> └─█─`%in%` 
#>   ├─x 
#>   └─y

R has over 30 infix operators divided into 18 precedence groups.
While the details are described in ?Syntax, very few people have memorized the complete ordering.
If there’s any confusion, use parentheses!

# override PEMDAS
lobstr::ast((1 + 2) * 3)
#> █─`*` 
#> ├─█─`(` 
#> │ └─█─`+` 
#> │   ├─1 
#> │   └─2 
#> └─3

The second source of ambiguity is introduced by repeated usage of the same infix function.

1 + 2 + 3
#> [1] 6

# What does R do first?
(1 + 2) + 3
#> [1] 6

# or
1 + (2 + 3)
#> [1] 6

In this case it doesn’t matter. Other places it might, like in ggplot2.
In R, most operators are left-associative, i.e., the operations on the left are evaluated first:

lobstr::ast(1 + 2 + 3)
#> █─`+` 
#> ├─█─`+` 
#> │ ├─1 
#> │ └─2 
#> └─3

There are two exceptions to the left-associative rule:
1. exponentiation
2. assignment

lobstr::ast(2 ^ 2 ^ 3)
#> █─`^` 
#> ├─2 
#> └─█─`^` 
#>   ├─2 
#>   └─3

lobstr::ast(x <- y <- z)
#> █─`<-` 
#> ├─x 
#> └─█─`<-` 
#>   ├─y 
#>   └─z

Parsing - turning characters you’ve typed into an AST (i.e., from strings to expressions).
R usually takes care of parsing code for us.
But occasionally you have code stored as a string, and you want to parse it yourself.
You can do so using rlang::parse_expr():

x1 <- "y <- x + 10"
x1
#> [1] "y <- x + 10"
is.call(x1)
#> [1] FALSE

x2 <- rlang::parse_expr(x1)
x2
#> y <- x + 10
is.call(x2)
#> [1] TRUE

parse_expr() always returns a single expression.
If you have multiple expression separated by ; or ,, you’ll need to use rlang::parse_exprs() which is the plural version of rlang::parse_expr(). It returns a list of expressions:

x3 <- "a <- 1; a + 1"

rlang::parse_exprs(x3)
#> [[1]]
#> a <- 1
#> 
#> [[2]]
#> a + 1

If you find yourself parsing strings into expressions often, quasiquotation may be a safer approach.
- More about quasiquaotation in Chapter 19.
The inverse of parsing is deparsing.
Deparsing - given an expression, you want the string that would generate it.
Deparsing happens automatically when you print an expression.
You can get the string with rlang::expr_text():
Parsing and deparsing are not symmetric.
- Parsing creates the AST which means that we lose backticks around ordinary names, comments, and whitespace.

cat(expr_text(expr({
  # This is a comment
  x <-             `x` + 1
})))
#> {
#>     x <- x + 1
#> }