18.2 Abstract Syntax Tree (AST)
- Expressions are objects that capture the structure of code without evaluating it.
- Expressions are also called abstract syntax trees (ASTs) because the structure of code is hierarchical and can be naturally represented as a tree.
- Understanding this tree structure is crucial for inspecting and modifying expressions.
- Branches = Calls
- Leaves = Symbols and constants
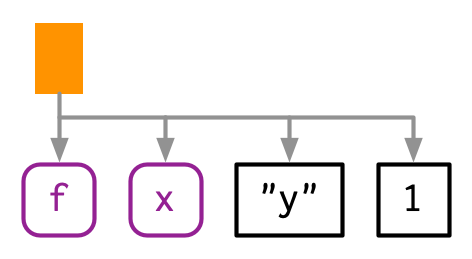
18.2.1 With lobstr::ast():
- Some functions might also contain more calls like the example below:
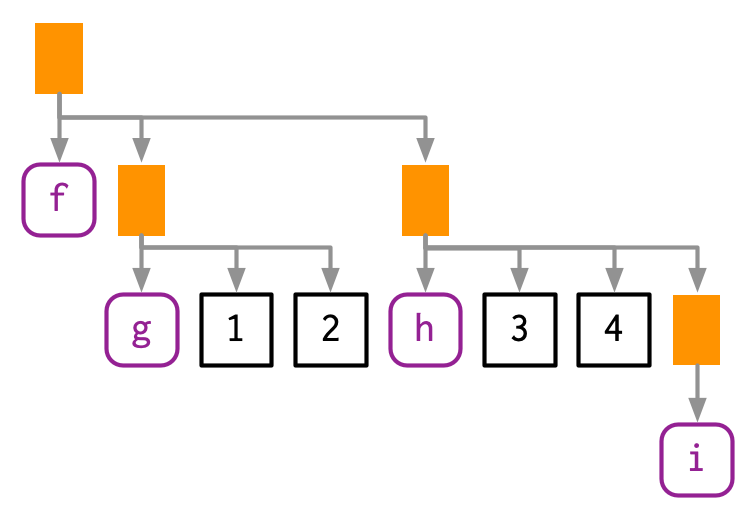
lobstr::ast(f(g(1, 2), h(3, 4, i())))
#> █─f
#> ├─█─g
#> │ ├─1
#> │ └─2
#> └─█─h
#> ├─3
#> ├─4
#> └─█─i- Read the hand-drawn diagrams from left-to-right (ignoring vertical position)
- Read the lobstr-drawn diagrams from top-to-bottom (ignoring horizontal position).
- The depth within the tree is determined by the nesting of function calls.
- Depth also determines evaluation order, as evaluation generally proceeds from deepest-to-shallowest, but this is not guaranteed because of lazy evaluation.
18.2.2 Infix calls
Every call in R can be written in tree form because any call can be written in prefix form.
An infix operator is a function where the function name is placed between its arguments. Prefix form is when then function name comes before the arguments, which are enclosed in parentheses. [Note that the name infix comes from the words prefix and suffix.]
- A characteristic of the language is that infix functions can always be written as prefix functions; therefore, all function calls can be represented using an AST.
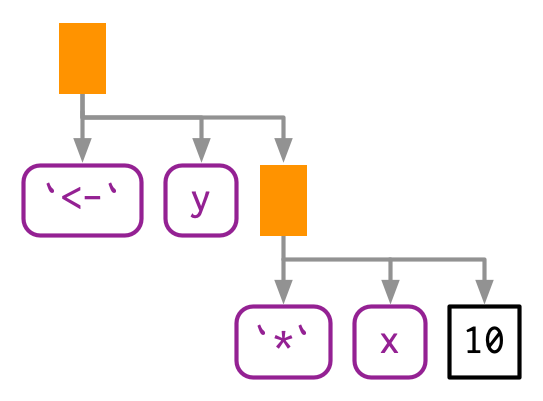
- There is no difference between the ASTs for the infix version vs the prefix version, and if you generate an expression with prefix calls, R will still print it in infix form: