5.8 Supervised Algorithm #2: Logistic Regression and Regularization

# fit logistic regression model
# method and family defines the type of regression
# in this case these arguments mean that we are doing logistic
# regression
lrFit = train(subtype ~ PDPN,  
               data=training, trControl=trainControl("none"),
               method="glm", family="binomial")

# create data to plot the sigmoid curve
newdat <- data.frame(PDPN=seq(min(training$PDPN),
                               max(training$PDPN),len=100))

# predict probabilities for the simulated data
newdat$subtype = predict(lrFit, newdata=newdat, type="prob")[,1]

# plot the sigmoid curve and the training data
plot(ifelse(subtype=="CIMP",1,0) ~ PDPN, 
     data=training, col="red4",
     ylab="subtype as 0 or 1", xlab="PDPN expression")
lines(subtype ~ PDPN, newdat, col="green4", lwd=2)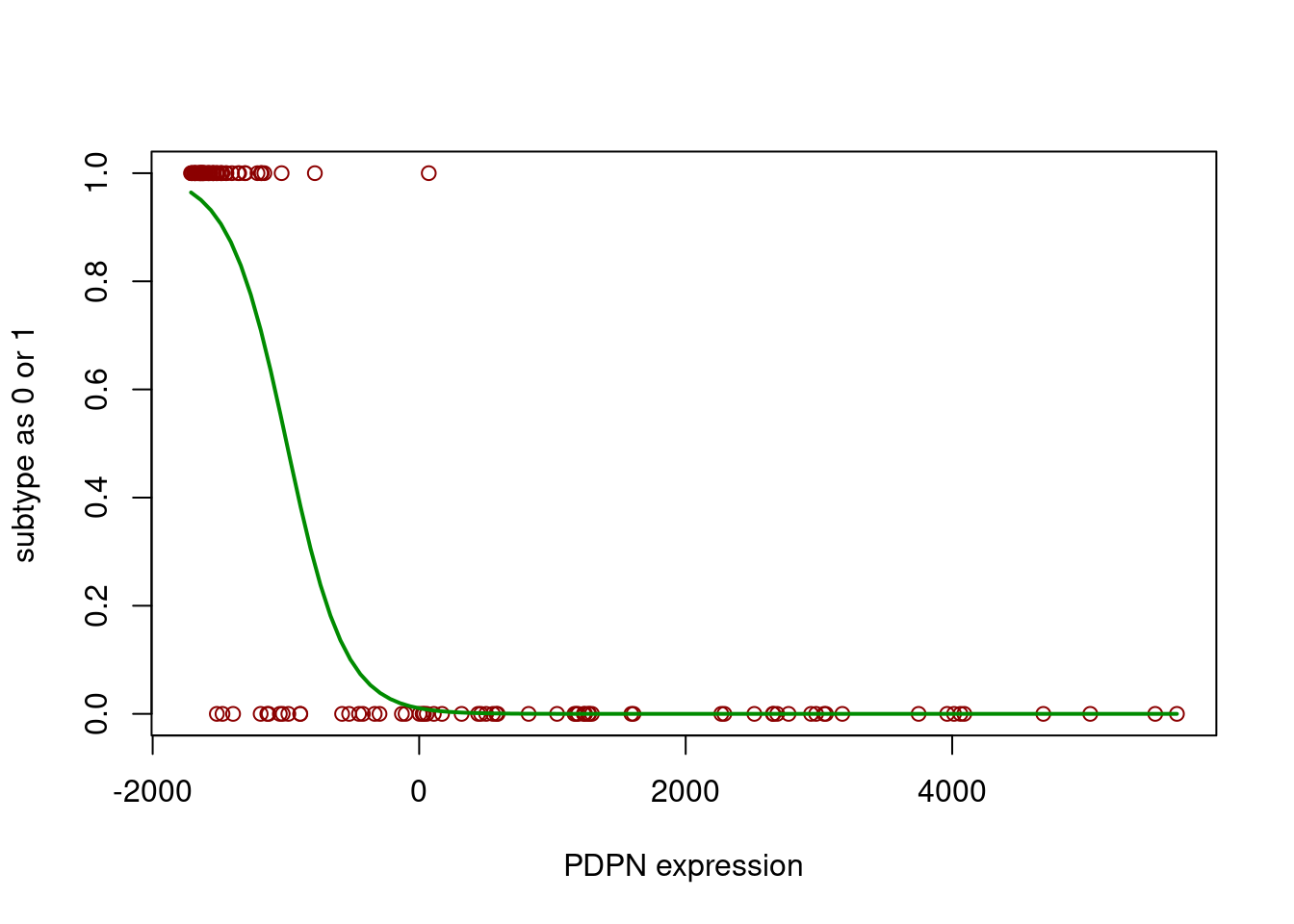

# training accuracy 
class.res=predict(lrFit,training[,-1])
confusionMatrix(training[,1],class.res)$overall[1]

##  Accuracy 
## 0.9230769

# test accuracy 
class.res=predict(lrFit,testing[,-1])
confusionMatrix(testing[,1],class.res)$overall[1]

##  Accuracy 
## 0.9259259

What if we didn’t train the model?

lrFit2 = train(subtype ~ .,  
                data=training, 
                # no model tuning with sampling
                trControl=trainControl("none"),
                method="glm", family="binomial")

# training accuracy 
class.res=predict(lrFit2,training[,-1])
confusionMatrix(training[,1],class.res)$overall[1]

## Accuracy 
##        1

# test accuracy 
class.res=predict(lrFit2,testing[,-1])
confusionMatrix(testing[,1],class.res)$overall[1]

##  Accuracy 
## 0.5185185

Decrease model variance by adding regularization. This limits the flexibility of the model.

L2 norm = Sqrt of sum of squared vector values –> coefficients in regression closer to zero.

Let’s try this!

set.seed(17)
library(glmnet)

## Loaded glmnet 4.1-8

# this method controls everything about training
# we will just set up 10-fold cross validation
trctrl <- trainControl(method = "cv",number=10)

# we will now train elastic net model
# it will try
enetFit <- train(subtype~., data = training, 
                 method = "glmnet",
                 trControl=trctrl,
                 # alpha and lambda paramters to try
                 tuneGrid = data.frame(alpha=0.5,
                                       lambda=seq(0.1,0.7,0.05)))

# best alpha and lambda values by cross-validation accuracy
enetFit$bestTune

##   alpha lambda
## 3   0.5    0.2

# test accuracy 
class.res=predict(enetFit,testing[,-1])
confusionMatrix(testing[,1],class.res)$overall[1]

##  Accuracy 
## 0.9074074

# most important variables
plot(varImp(enetFit),top=10)