15.4 The rgeoda package

library(rgeoda)
Geoda_w <- queen_weights(pol_pres15)
summary(Geoda_w)

##                      name               value
## 1 number of observations:                2495
## 2          is symmetric:                 TRUE
## 3               sparsity: 0.00228786229774178
## 4        # min neighbors:                   1
## 5        # max neighbors:                  13
## 6       # mean neighbors:    5.70821643286573
## 7     # median neighbors:                   6
## 8           has isolates:               FALSE

?queen_weights

Local Multivariate Geary Statistics

?local_multigeary

library(parallel)
lisa <- local_multigeary(Geoda_w, 
    pol_pres15[c("I_turnout", "II_turnout")], 
    cpu_threads = max(detectCores() - 1, 1),
    permutations = 99999, 
    seed = 1)

all.equal(card(nb_q), 
          lisa_num_nbrs(lisa), 
          check.attributes = FALSE)

## [1] TRUE

Let’s use the Local Geary’s measure to compute local adaptation of Geary’s C statistic of spatial autocorrelation.

The Local Geary uses squared differences to measure dissimilarity unlike the Local Moran. Low values of the Local Geary indicate positive spatial autocorrelation and large refers to negative spatial autocorrelation.

?localC_perm returns a pseudo p-value

lw_q_W <- nb_q |> 
        nb2listw(style = "W")

locMvC_p <- pol_pres15 |> 
        st_drop_geometry() |> 
        subset(select = c(I_turnout, II_turnout)) |>
        localC_perm(lw_q_W, nsim=9999, iseed=1) 

all.equal(lisa_values(lisa), 
          c(locMvC_p),
          check.attributes = FALSE)

## [1] TRUE

apply(attr(locMvC_p, "pseudo-p")[,c("Pr(z != E(Ci)) Sim", 
                                "Pr(folded) Sim")], 2, range)

##      Pr(z != E(Ci)) Sim Pr(folded) Sim
## [1,]             0.0002         0.0001
## [2,]             0.9984         0.4992

pol_pres15$hs_MvCa <- locMvC_p |> 
  hotspot(Prname = "Pr(folded) Sim",
                    cutoff = 0.0025)

mvc <- factor(lisa_clusters(lisa), levels=0:2,
              labels = lisa_labels(lisa)[1:3])

is.na(mvc) <- p.adjust(lisa_pvalues(lisa), "fdr") >= 0.0025

pol_pres15$geoda_mvc <- droplevels(mvc)

addmargins(table(spdep = addNA(pol_pres15$hs_MvCa),
                 rgeoda = addNA(pol_pres15$geoda_mvc)))

##           rgeoda
## spdep      Positive <NA>  Sum
##   Positive      255    4  259
##   <NA>           67 2169 2236
##   Sum           322 2173 2495

library(tmap)

m5 <- tm_shape(pol_pres15) +
    tm_fill("hs_MvCa", 
            palette = RColorBrewer::brewer.pal(4, "Set3")[c(4, 1)],
            colorNA = "grey95", 
            textNA = "Not \"interesting\"",
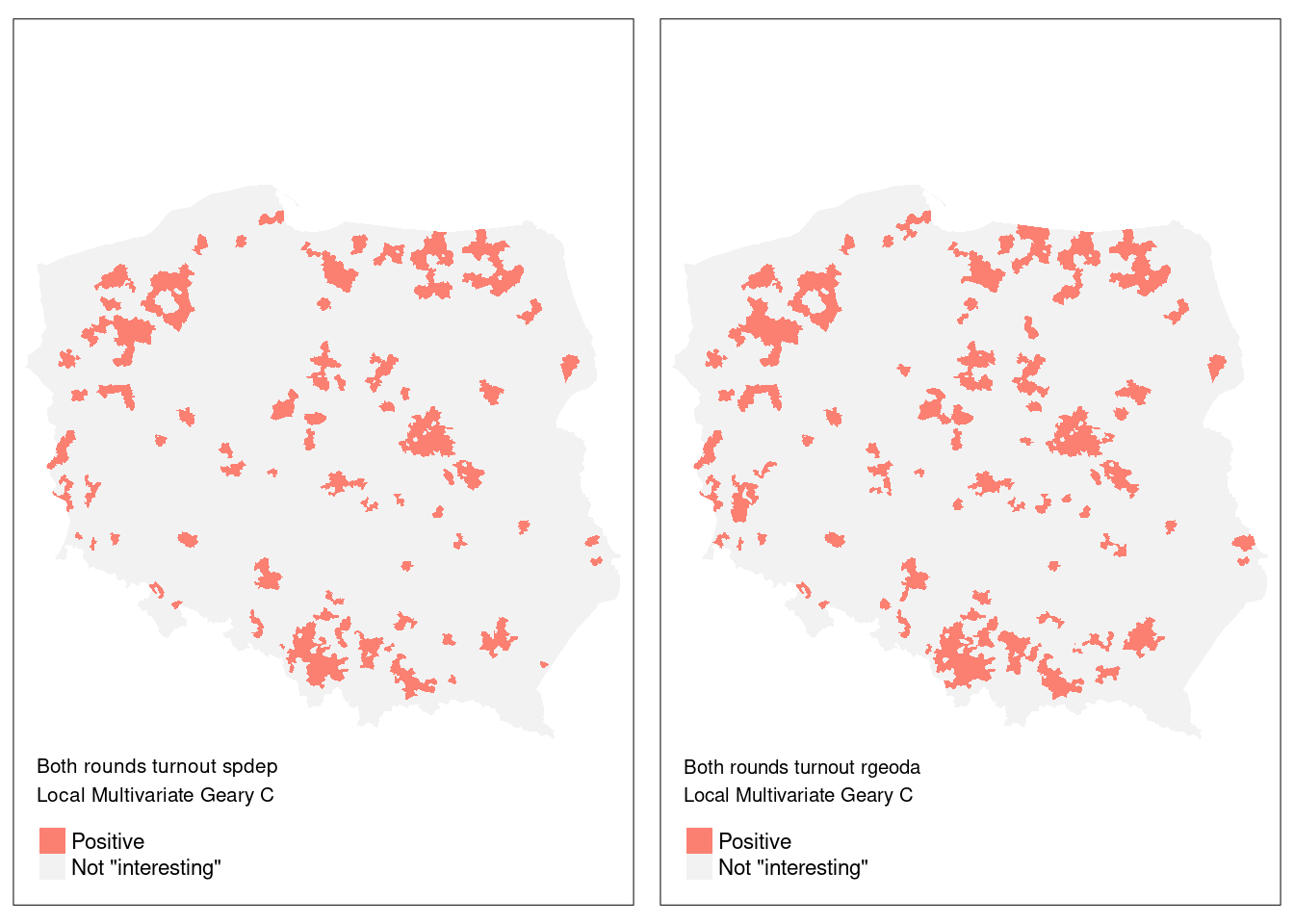
  title = "Both rounds turnout spdep\nLocal Multivariate Geary C")

m6 <- tm_shape(pol_pres15) +
    tm_fill("geoda_mvc", 
        palette = RColorBrewer::brewer.pal(4, "Set3")[c(4, 1)],
        colorNA = "grey95", 
        textNA = "Not \"interesting\"",
  title="Both rounds turnout rgeoda\nLocal Multivariate Geary C")

tmap_arrange(m5, m6, nrow=1)