Dimensions, attributes, and support

• Depending on the data that we are dealing with (discrete or continuous), we may have the following data structures:
  • time series, depicted as time lines for functions of time
    
  • image or raster data for two-dimensional spatial data
    
  • time sequences of images for dynamic spatial data (spatio-temporal array or data cube)

Here, a variable Z depends on x,y, and t. The variables from the range (x,y,t) are the cube dimensions.

$$Z = f(x,y,t)$$

$$\{ Z_1, Z_2, ..., Z_p \} = f(x,y,t)$$

And if we have multiple time dimensions then we represent each with $D_x$. For example, when we are splitting time in years, day-of-year, hour-of-day.

$$\{ Z_1, Z_2, ..., Z_p \} = f(D_1, D_2, ... , D_n)$$

We deal with datasets with one or more space dimensions and zero or more time dimensions as data cubes:

• simple features

• time series for sets of features

• raster data

• multi-spectral raster data (images)

• time series of multi-spectral raster data (video)

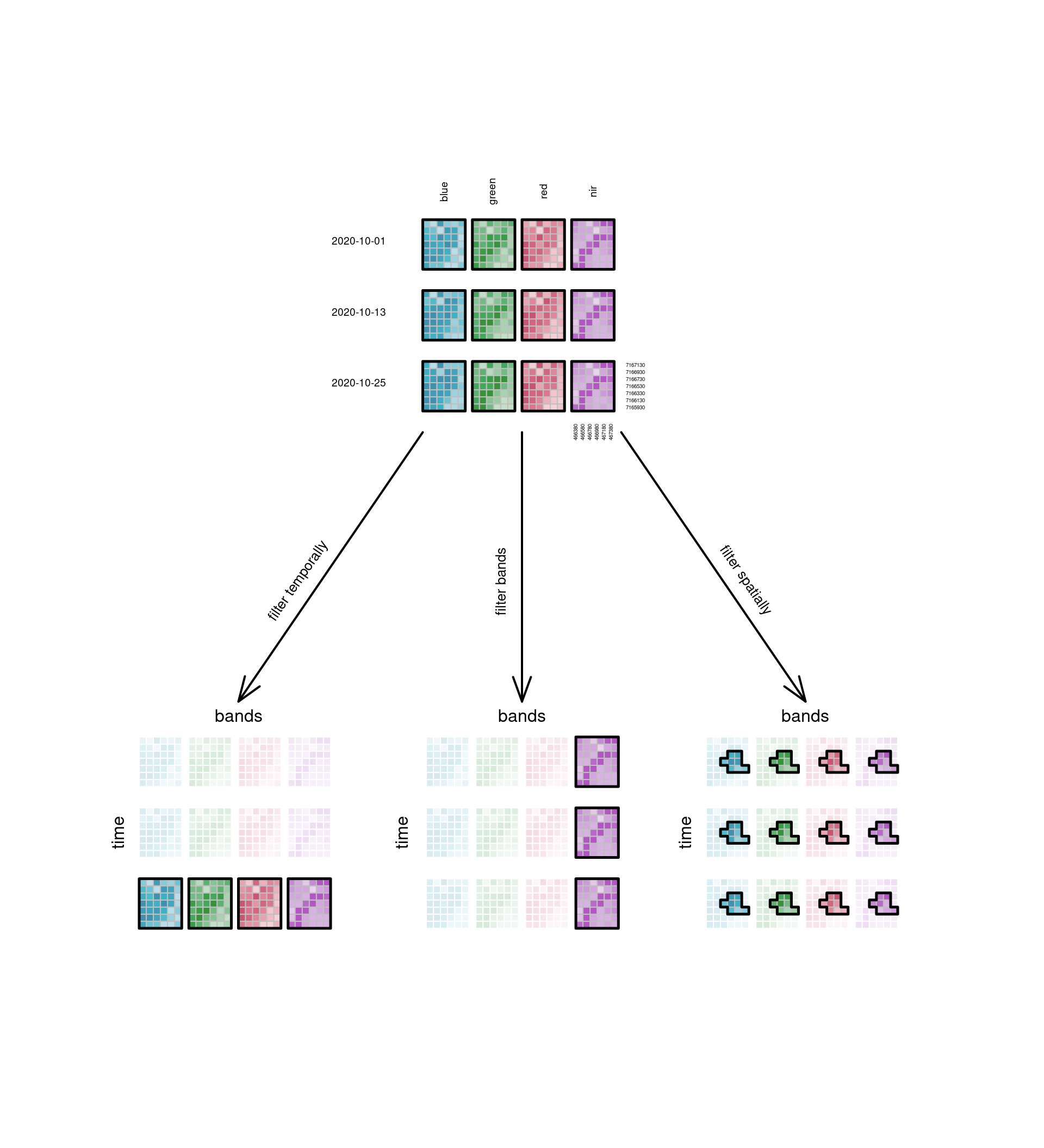
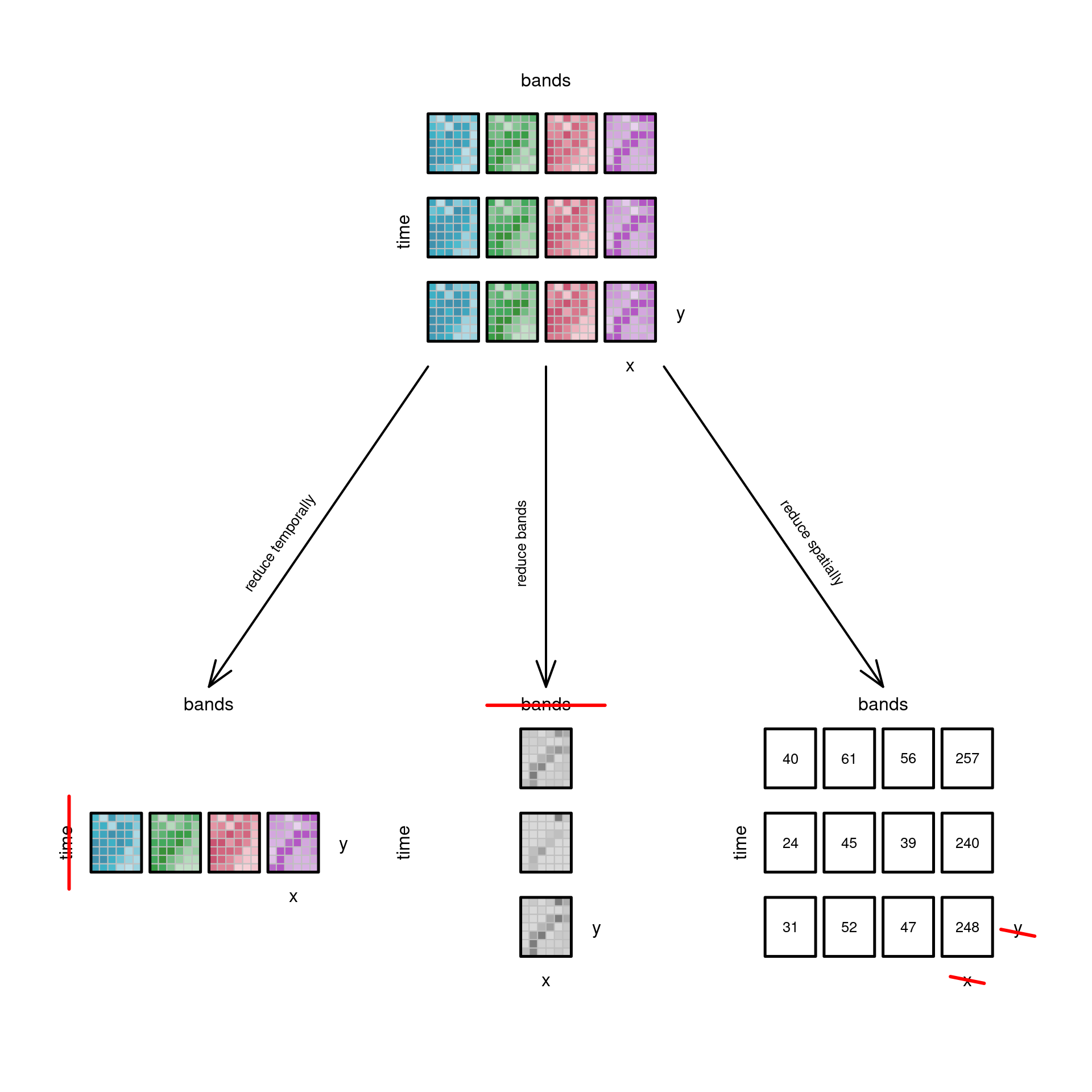
  Operations on data cubes

Slicing a cube: filter

• Data cubes can be sliced into sub-cubes by fixing a dimension at a particular value.

Applying functions to dimensions

• Functions such as abs, sin, or sqrt is applied to all values in the cube.
  
• Summarising functions such as mean to the entire cube and returns a single value/s.

Reducing dimensions

• When applying a function like mean the cube reduces its dimensionality to zero.
  
• The following example shows estimating NDVI across time, bands, or averaging all pixels on each raster.