10.7 Exercise 1

Use a random forest model to predict SID values (e.g. using package randomForest), and plot the random forest predictions against observations, along with the line.

library(randomForest) |> suppressPackageStartupMessages()

r = randomForest(SID ~ NWB, nc1)

nc1$rf = predict(r)

nc2 <- nc1%>%
  dplyr::select(SID,rf)

nc2%>%head

## Simple feature collection with 6 features and 2 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -81.74107 ymin: 36.07282 xmax: -75.77316 ymax: 36.58965
## Geodetic CRS:  NAD27
## # A tibble: 6 × 3
##        SID       rf                                                         geom
##      <dbl>    <dbl>                                           <MULTIPOLYGON [°]>
## 1 0.000917 0.000666 (((-81.47276 36.23436, -81.54084 36.27251, -81.56198 36.273…
## 2 0        0.000518 (((-81.23989 36.36536, -81.24069 36.37942, -81.26284 36.405…
## 3 0.00157  0.00179  (((-80.45634 36.24256, -80.47639 36.25473, -80.53688 36.256…
## 4 0.00197  0.00110  (((-76.00897 36.3196, -76.01735 36.33773, -76.03288 36.3359…
## 5 0.00633  0.00442  (((-77.21767 36.24098, -77.23461 36.2146, -77.29861 36.2115…
## 6 0.00482  0.00479  (((-76.74506 36.23392, -76.98069 36.23024, -76.99475 36.235…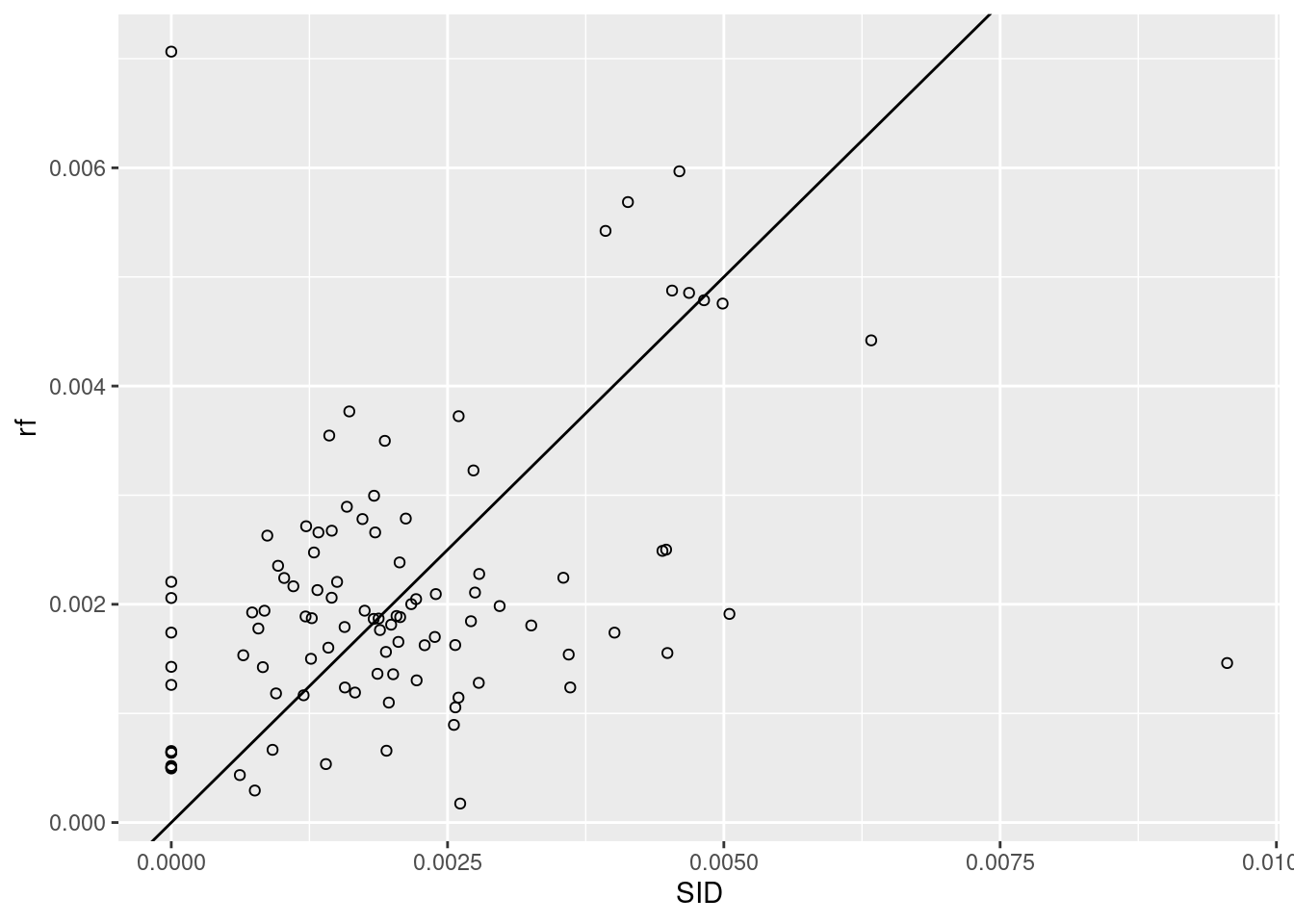

nc2 %>%
  ggplot(aes(SID,rf))+
  geom_point(shape=21,stroke=0.5)+
  geom_abline()

10.7.1 Exercise 2

Create a new dataset by randomly sampling 1000 points from the nc dataset, and rerun the linear regression model of section 10.2 on this dataset. What has changed?

pts = st_sample(nc, 1000)
nc3 = st_intersection(nc1, pts)

## Warning: attribute variables are assumed to be spatially constant throughout
## all geometries

fit |> summary()

## 
## Call:
## lm(formula = SID ~ NWB, data = nc1)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0033253 -0.0007411 -0.0000691  0.0005479  0.0062218 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.0006773  0.0002327   2.910  0.00447 ** 
## NWB         0.0043785  0.0006204   7.058 2.44e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.001288 on 98 degrees of freedom
## Multiple R-squared:  0.337,  Adjusted R-squared:  0.3302 
## F-statistic: 49.82 on 1 and 98 DF,  p-value: 2.438e-10

fit2 <- lm(SID ~ NWB, nc3) 

fit2|> summary()

## 
## Call:
## lm(formula = SID ~ NWB, data = nc3)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0033493 -0.0007691 -0.0000141  0.0005032  0.0061979 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.140e-04  7.126e-05   10.02   <2e-16 ***
## NWB         4.358e-03  1.846e-04   23.60   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.001158 on 998 degrees of freedom
## Multiple R-squared:  0.3582, Adjusted R-squared:  0.3576 
## F-statistic:   557 on 1 and 998 DF,  p-value: < 2.2e-16

the standard error has decreased with a factor 3 (sqrt(10))

lm(SID ~ NWB, nc1) |>
  predict(nc1, interval = "prediction") -> pr1
lm(SID ~ NWB, nc3) |>
  predict(nc1, interval = "prediction") -> pr2
mean(pr1[,"upr"] - pr1[,"lwr"])

## [1] 0.005161177

# [1] 0.005161177
mean(pr2[,"upr"] - pr2[,"lwr"])

## [1] 0.004550376

# [1] 0.004992217

lm(SID ~ NWB, nc1) |>
  predict(nc1, interval = "confidence") -> pr1
lm(SID ~ NWB, nc3) |>
  predict(nc1, interval = "confidence") -> pr2
mean(pr1[,"upr"] - pr1[,"lwr"])

## [1] 0.0007025904

# [1] 0.0007025904
mean(pr2[,"upr"] - pr2[,"lwr"])

## [1] 0.00020215

# [1] 0.000221525

10.7.2 Exercise 3

Do the water-land classification using class::knn.

tif <- system.file("tif/L7_ETMs.tif", package = "stars")

library(stars)
# r <- read_stars(tif)
(r <- read_stars(tif))

## stars object with 3 dimensions and 1 attribute
## attribute(s):
##              Min. 1st Qu. Median     Mean 3rd Qu. Max.
## L7_ETMs.tif     1      54     69 68.91242      86  255
## dimension(s):
##      from  to  offset delta                     refsys point x/y
## x       1 349  288776  28.5 SIRGAS 2000 / UTM zone 25S FALSE [x]
## y       1 352 9120761 -28.5 SIRGAS 2000 / UTM zone 25S FALSE [y]
## band    1   6      NA    NA                         NA    NA

st_bbox(r)

##      xmin      ymin      xmax      ymax 
##  288776.3 9110728.8  298722.8 9120760.8

st_bbox(r) |> 
  st_as_sfc()

## Geometry set for 1 feature 
## Geometry type: POLYGON
## Dimension:     XY
## Bounding box:  xmin: 288776.3 ymin: 9110729 xmax: 298722.8 ymax: 9120761
## Projected CRS: SIRGAS 2000 / UTM zone 25S

## POLYGON ((288776.3 9110729, 298722.8 9110729, 2...

set.seed(115517)
pts2 <- st_bbox(r) |> 
  st_as_sfc() |> 
  st_sample(20)

(e <- st_extract(r, pts2))

## stars object with 2 dimensions and 1 attribute
## attribute(s):
##              Min. 1st Qu. Median     Mean 3rd Qu. Max.
## L7_ETMs.tif    12   41.75     63 60.95833    80.5  145
## dimension(s):
##          from to                     refsys point
## geometry    1 20 SIRGAS 2000 / UTM zone 25S  TRUE
## band        1  6                         NA    NA
##                                                         values
## geometry POINT (293002.2 9115516),...,POINT (290941.1 9114128)
## band                                                      NULL

r%>%class

## [1] "stars"

r%>%dim

##    x    y band 
##  349  352    6

st_as_sf(e)

## Simple feature collection with 20 features and 6 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 289053.6 ymin: 9110888 xmax: 298629.5 ymax: 9120451
## Projected CRS: SIRGAS 2000 / UTM zone 25S
## First 10 features:
##    L7_ETMs.tif.V1 L7_ETMs.tif.V2 L7_ETMs.tif.V3 L7_ETMs.tif.V4 L7_ETMs.tif.V5
## 1              69             59             53             75             78
## 2              71             60             59             23             18
## 3              63             52             39             87             71
## 4              66             54             41             87             84
## 5              84             70             73             58            126
## 6              59             44             31             67             63
## 7              58             42             31             67             55
## 8             102             93             65             13             15
## 9              83             71             80             69            127
## 10             61             46             36             76             63
##    L7_ETMs.tif.V6                 geometry
## 1              45 POINT (293002.2 9115516)
## 2              13 POINT (290053.1 9110930)
## 3              33 POINT (292911.6 9119069)
## 4              42 POINT (292503.2 9116861)
## 5             102 POINT (291435.7 9113502)
## 6              30 POINT (294899.2 9116963)
## 7              27 POINT (291231.8 9118336)
## 8              13 POINT (298629.5 9112151)
## 9             110 POINT (295431.9 9119798)
## 10             33   POINT (292282 9118130)

e_df <- st_as_sf(e) |> 
  st_coordinates() %>%
  as_tibble() %>%
  mutate(label=c(1:20),
         group=ifelse(label%in%c(8, 14, 15, 18, 19),"land","water"))

e_df%>%head

## # A tibble: 6 × 4
##         X        Y label group
##     <dbl>    <dbl> <int> <chr>
## 1 293002. 9115516.     1 water
## 2 290053. 9110930.     2 water
## 3 292912. 9119069.     3 water
## 4 292503. 9116861.     4 water
## 5 291436. 9113502.     5 water
## 6 294899. 9116963.     6 water

ggplot()+
  stars::geom_stars(data=r)+
  geom_text(data=e_df,
            mapping=aes(x=X,y=Y,
                        label=label,
                        group=group,
                        color=group),
            check_overlap = T,
            inherit.aes = F)+
  scale_color_manual(values=c("red","yellow"))+
  coord_equal()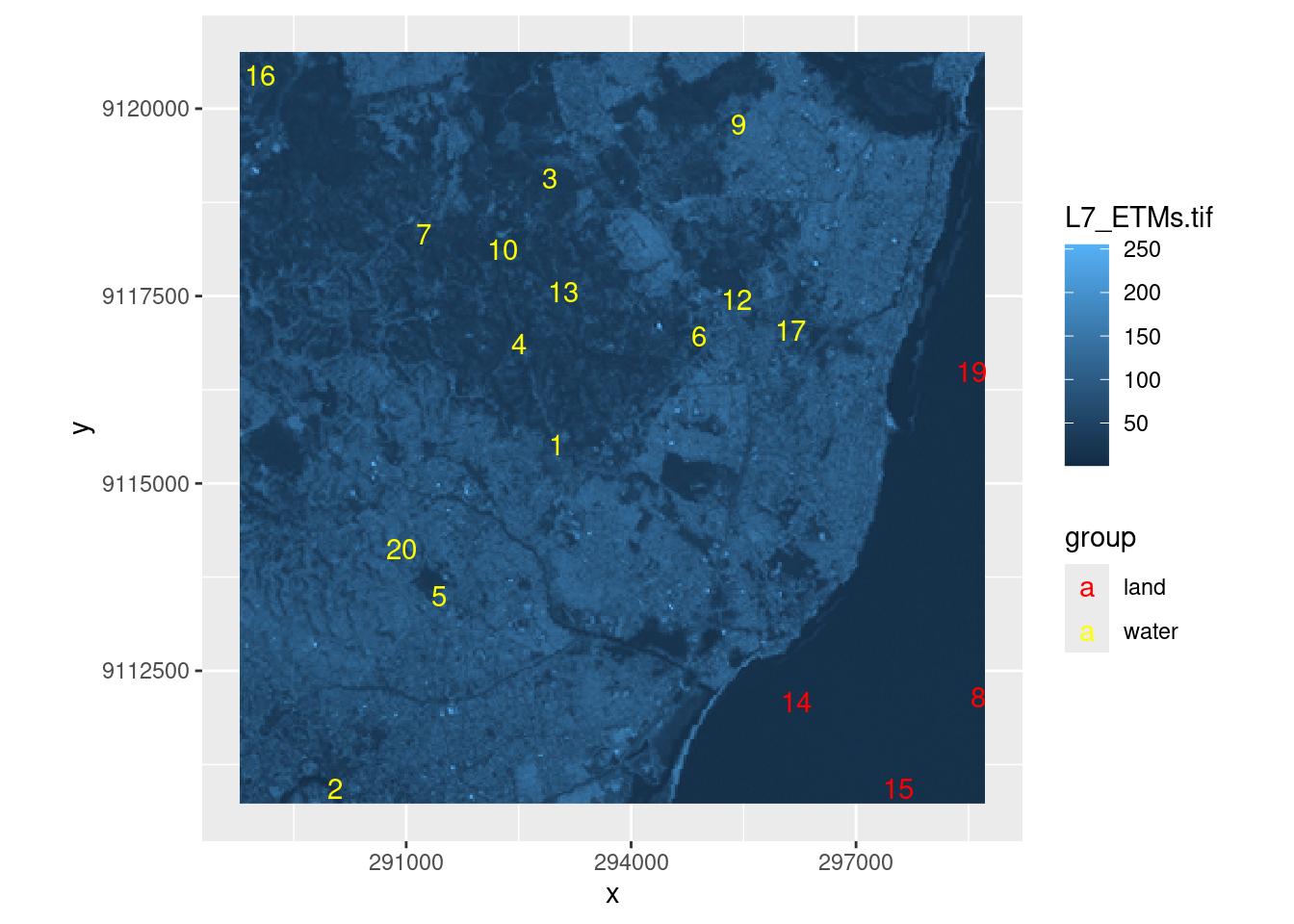

rs <- split(r)
rs

## stars object with 2 dimensions and 6 attributes
## attribute(s):
##     Min. 1st Qu. Median     Mean 3rd Qu. Max.
## X1    47      67     78 79.14772      89  255
## X2    32      55     66 67.57465      79  255
## X3    21      49     63 64.35886      77  255
## X4     9      52     63 59.23541      75  255
## X5     1      63     89 83.18266     112  255
## X6     1      32     60 59.97521      88  255
## dimension(s):
##   from  to  offset delta                     refsys point x/y
## x    1 349  288776  28.5 SIRGAS 2000 / UTM zone 25S FALSE [x]
## y    1 352 9120761 -28.5 SIRGAS 2000 / UTM zone 25S FALSE [y]

trn <- rs %>%
  st_extract(pts2)

trn$cls <- rep("land", 20)
trn$cls[c(8, 14, 15, 18, 19)] <- "water"

library(class)
tr <- as.data.frame(trn) |> dplyr::select(X1, X2, X3, X4, X5, X6) 
test <- as.data.frame(rs) |> dplyr::select(X1, X2, X3, X4, X5, X6)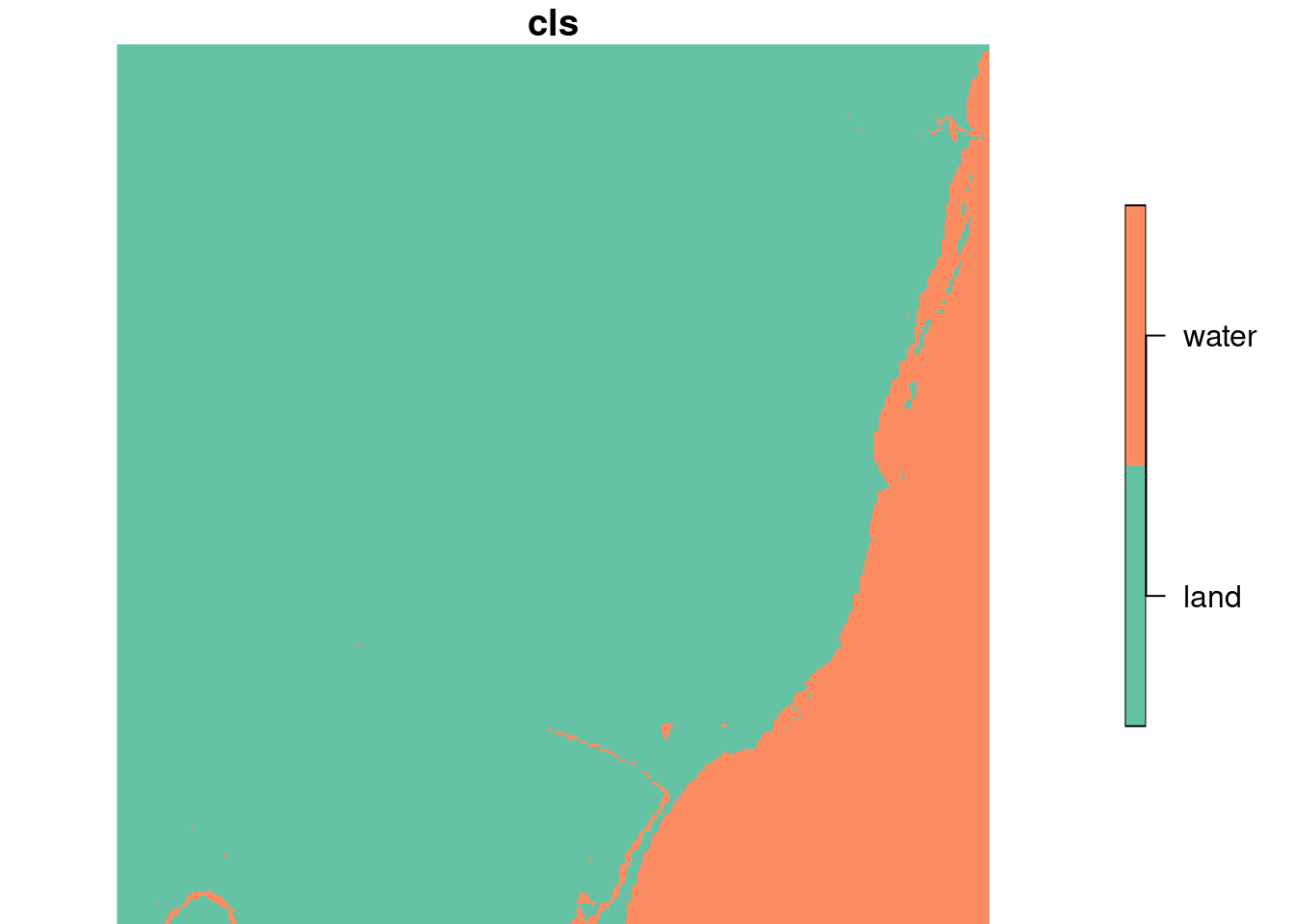 

rs$cls = knn(tr, test, trn$cl, k = 5)
plot(rs["cls"])

10.7.3 Exercise 4

For the linear model using nc and for the knn example of the previous exercise, add a first and a second order linear model in the spatial coordinates and compare the results (use st_centroid to obtain polygon centroids, and st_coordinates to extract the x and y coordinates in matrix form).

nc1

## Simple feature collection with 100 features and 17 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: -84.32385 ymin: 33.88199 xmax: -75.45698 ymax: 36.58965
## Geodetic CRS:  NAD27
## # A tibble: 100 × 18
##     AREA PERIMETER CNTY_ CNTY_ID NAME  FIPS  FIPSNO CRESS_ID BIR74 SID74 NWBIR74
##  * <dbl>     <dbl> <dbl>   <dbl> <chr> <chr>  <dbl>    <int> <dbl> <dbl>   <dbl>
##  1 0.114      1.44  1825    1825 Ashe  37009  37009        5  1091     1      10
##  2 0.061      1.23  1827    1827 Alle… 37005  37005        3   487     0      10
##  3 0.143      1.63  1828    1828 Surry 37171  37171       86  3188     5     208
##  4 0.07       2.97  1831    1831 Curr… 37053  37053       27   508     1     123
##  5 0.153      2.21  1832    1832 Nort… 37131  37131       66  1421     9    1066
##  6 0.097      1.67  1833    1833 Hert… 37091  37091       46  1452     7     954
##  7 0.062      1.55  1834    1834 Camd… 37029  37029       15   286     0     115
##  8 0.091      1.28  1835    1835 Gates 37073  37073       37   420     0     254
##  9 0.118      1.42  1836    1836 Warr… 37185  37185       93   968     4     748
## 10 0.124      1.43  1837    1837 Stok… 37169  37169       85  1612     1     160
## # ℹ 90 more rows
## # ℹ 7 more variables: BIR79 <dbl>, SID79 <dbl>, NWBIR79 <dbl>,
## #   geom <MULTIPOLYGON [°]>, SID <dbl>, NWB <dbl>, rf <dbl>

cc <- st_centroid(nc1) |> 
  st_coordinates() 

## Warning: st_centroid assumes attributes are constant over geometries

cc

##                X        Y
##   [1,] -81.49823 36.43140
##   [2,] -81.12513 36.49111
##   [3,] -80.68573 36.41252
##   [4,] -76.02719 36.40714
##   [5,] -77.41046 36.42236
##   [6,] -76.99472 36.36142
##   [7,] -76.23402 36.40122
##   [8,] -76.70446 36.44428
##   [9,] -78.11042 36.39693
##  [10,] -80.23429 36.40042
##  [11,] -79.33478 36.39346
##  [12,] -79.77039 36.39610
##  [13,] -78.65648 36.29993
##  [14,] -78.97685 36.38870
##  [15,] -78.41129 36.36224
##  [16,] -77.65599 36.25302
##  [17,] -76.31443 36.31231
##  [18,] -81.15971 36.20158
##  [19,] -81.69125 36.22481
##  [20,] -76.45458 36.20486
##  [21,] -76.61642 36.14886
##  [22,] -81.92145 36.07194
##  [23,] -80.66413 36.15481
##  [24,] -78.28707 36.07760
##  [25,] -80.25335 36.12571
##  [26,] -79.78279 36.07305
##  [27,] -79.39793 36.03757
##  [28,] -76.98470 36.06189
##  [29,] -79.12178 36.05355
##  [30,] -78.87809 36.02862
##  [31,] -77.98691 35.96228
##  [32,] -82.16321 36.00591
##  [33,] -77.59821 35.90717
##  [34,] -81.54356 35.94703
##  [35,] -82.30763 35.89215
##  [36,] -77.10745 35.83637
##  [37,] -78.65299 35.78443
##  [38,] -82.70541 35.85323
##  [39,] -80.87108 35.80259
##  [40,] -80.54155 35.92495
##  [41,] -81.17403 35.91575
##  [42,] -80.20823 35.78986
##  [43,] -81.70198 35.74484
##  [44,] -76.58303 35.82508
##  [45,] -76.21986 35.80954
##  [46,] -82.04495 35.67528
##  [47,] -79.80374 35.70551
##  [48,] -79.25672 35.69645
##  [49,] -77.92280 35.69918
##  [50,] -80.51921 35.63691
##  [51,] -77.37784 35.58906
##  [52,] -81.21380 35.65816
##  [53,] -82.52831 35.60684
##  [54,] -78.36673 35.51338
##  [55,] -82.98086 35.55136
##  [56,] -75.80950 35.73533
##  [57,] -76.87093 35.49589
##  [58,] -83.48992 35.48069
##  [59,] -77.67887 35.48228
##  [60,] -79.17379 35.47106
##  [61,] -81.91783 35.39871
##  [62,] -78.00728 35.35727
##  [63,] -78.87102 35.36660
##  [64,] -81.54942 35.32956
##  [65,] -81.22074 35.48086
##  [66,] -83.13929 35.28244
##  [67,] -79.47828 35.30615
##  [68,] -80.82937 35.24481
##  [69,] -80.55085 35.38494
##  [70,] -79.90276 35.32716
##  [71,] -80.24928 35.31388
##  [72,] -82.47627 35.33467
##  [73,] -83.82962 35.34507
##  [74,] -77.64556 35.23278
##  [75,] -82.79526 35.19968
##  [76,] -81.17520 35.29245
##  [77,] -82.17027 35.27570
##  [78,] -83.42226 35.14516
##  [79,] -78.36970 34.98647
##  [80,] -76.76886 35.13564
##  [81,] -84.05986 35.13111
##  [82,] -78.82647 35.04375
##  [83,] -77.35617 35.01856
##  [84,] -80.53145 34.98630
##  [85,] -80.10405 34.97520
##  [86,] -79.23592 35.01163
##  [87,] -76.24694 35.53213
##  [88,] -77.93356 34.93235
##  [89,] -79.74228 35.00140
##  [90,] -83.74725 35.05384
##  [91,] -77.10388 35.13065
##  [92,] -79.47719 34.83945
##  [93,] -77.44295 34.73908
##  [94,] -79.10106 34.63869
##  [95,] -76.69587 34.81997
##  [96,] -78.55994 34.60928
##  [97,] -77.91626 34.52688
##  [98,] -78.65478 34.26335
##  [99,] -77.89580 34.26162
## [100,] -78.25090 34.07671

# geometries
nc4 <- bind_cols(nc1, cc) |> 
  transmute(X=X, Y=Y, SID=SID, NWB=NWB) 

(lm0 <- lm(SID ~ NWB, nc1)) |> summary()

## 
## Call:
## lm(formula = SID ~ NWB, data = nc1)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0033253 -0.0007411 -0.0000691  0.0005479  0.0062218 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.0006773  0.0002327   2.910  0.00447 ** 
## NWB         0.0043785  0.0006204   7.058 2.44e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.001288 on 98 degrees of freedom
## Multiple R-squared:  0.337,  Adjusted R-squared:  0.3302 
## F-statistic: 49.82 on 1 and 98 DF,  p-value: 2.438e-10

(lm1 <- lm(SID ~ NWB + X + Y, nc4)) |> summary()

## 
## Call:
## lm(formula = SID ~ NWB + X + Y, data = nc4)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0027669 -0.0007998 -0.0001568  0.0006015  0.0053235 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.248e-03  1.050e-02  -0.119  0.90564    
## NWB          5.950e-03  7.983e-04   7.454 3.99e-11 ***
## X           -2.266e-04  7.794e-05  -2.907  0.00453 ** 
## Y           -4.655e-04  2.167e-04  -2.148  0.03424 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.001213 on 96 degrees of freedom
## Multiple R-squared:  0.424,  Adjusted R-squared:  0.406 
## F-statistic: 23.56 on 3 and 96 DF,  p-value: 1.645e-11

(lm2 <- lm(SID ~ NWB+X+Y+ I(X^2) + I(Y^2)+ X*Y, nc4)) |> summary()

## 
## Call:
## lm(formula = SID ~ NWB + X + Y + I(X^2) + I(Y^2) + X * Y, data = nc4)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0027759 -0.0007526 -0.0001441  0.0006399  0.0053102 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.703e-01  7.119e-01   0.661    0.511    
## NWB          5.978e-03  9.463e-04   6.317 9.08e-09 ***
## X           -2.632e-04  1.016e-02  -0.026    0.979    
## Y           -2.719e-02  2.576e-02  -1.055    0.294    
## I(X^2)      -1.064e-05  3.387e-05  -0.314    0.754    
## I(Y^2)       3.240e-04  3.445e-04   0.941    0.349    
## X:Y         -4.714e-05  1.688e-04  -0.279    0.781    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.001221 on 93 degrees of freedom
## Multiple R-squared:  0.4339, Adjusted R-squared:  0.3974 
## F-statistic: 11.88 on 6 and 93 DF,  p-value: 7.383e-10

nc1$prediction_0 <- lm0 |> predict(nc4)
nc1$prediction_1 <- lm1 |> predict(nc4)
nc1$prediction_2 <- lm2 |> predict(nc4)

nc5 <- nc1 %>%
  dplyr::select(prediction_0,prediction_1,prediction_2) |>
  #pivot_longer(cols = c("pr0","pr1","pr2"))%>%
  st_as_stars() |> 
  merge() 

nc5 

## stars object with 2 dimensions and 1 attribute
## attribute(s):
##                                          Min.    1st Qu.      Median
## prediction_0.prediction_1.p...  -0.0005071205 0.00127737 0.002034891
##                                        Mean     3rd Qu.       Max.
## prediction_0.prediction_1.p...  0.002045596 0.002776815 0.00517751
## dimension(s):
##            from  to refsys point
## geom          1 100  NAD27 FALSE
## attributes    1   3     NA    NA
##                                                                   values
## geom       MULTIPOLYGON (((-81.47276...,...,MULTIPOLYGON (((-78.65572...
## attributes                      prediction_0, prediction_1, prediction_2

ggplot()+
  geom_stars(data=nc5)+
  facet_wrap(~attributes,ncol = 1) +
  scale_fill_viridis_c()+
  labs(fill="")+
  theme_void()+
  theme(legend.position = "bottom",
        legend.text = element_text(size=3))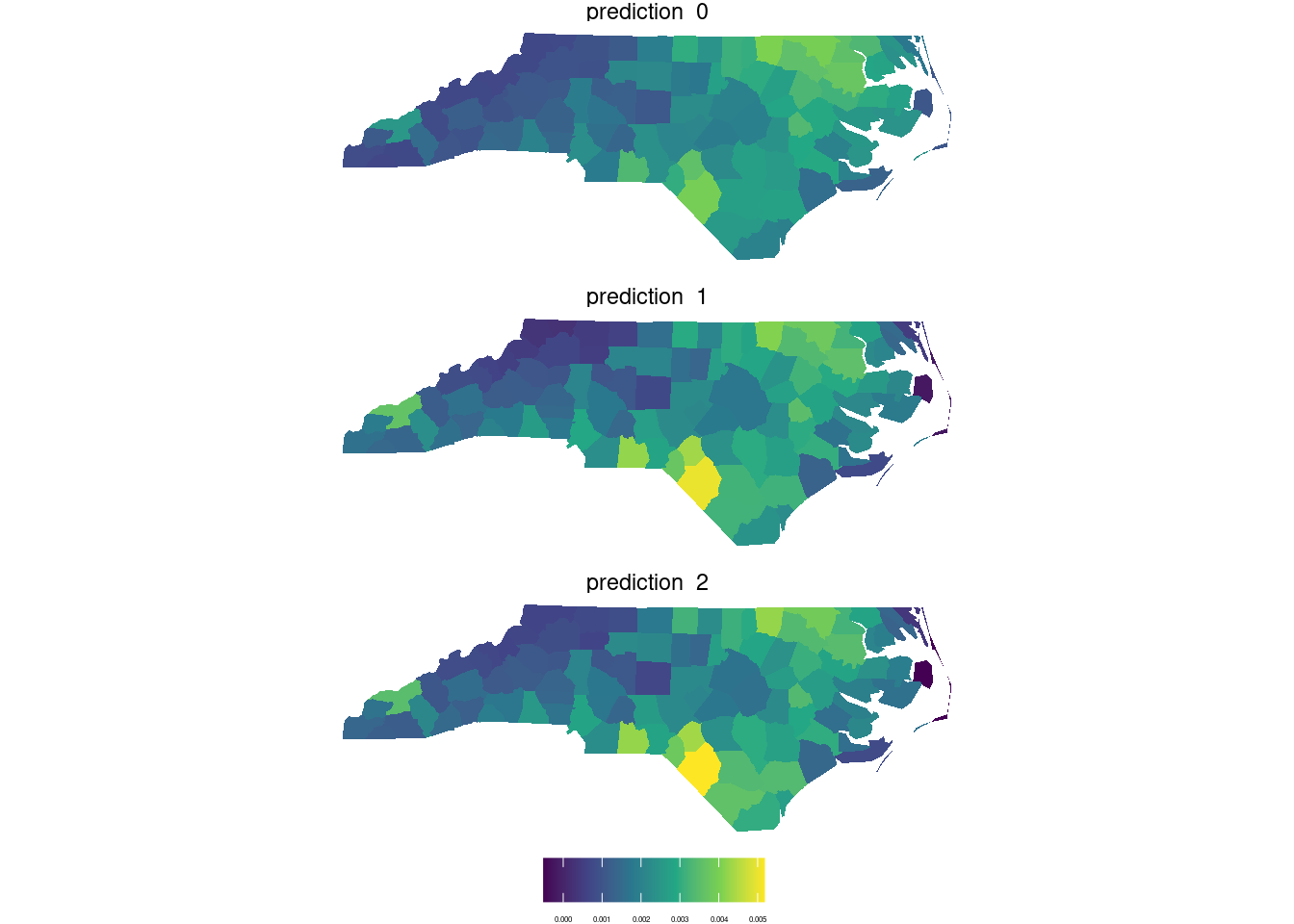

tr1 <- cbind(as.data.frame(trn), 
             st_coordinates(trn)) |> 
  dplyr::select(X, Y, X1, X2, X3, X4, X5, X6) 

test1 <- as.data.frame(rs) |> 
  transmute(X=x, Y=y, X1, X2, X3, X4, X5, X6)

rs$cls1 = knn(tr1, test1, trn$cl, k = 5)

rs

## stars object with 2 dimensions and 8 attributes
## attribute(s):
##       X1               X2               X3               X4         
##  Min.   : 47.00   Min.   : 32.00   Min.   : 21.00   Min.   :  9.00  
##  1st Qu.: 67.00   1st Qu.: 55.00   1st Qu.: 49.00   1st Qu.: 52.00  
##  Median : 78.00   Median : 66.00   Median : 63.00   Median : 63.00  
##  Mean   : 79.15   Mean   : 67.57   Mean   : 64.36   Mean   : 59.24  
##  3rd Qu.: 89.00   3rd Qu.: 79.00   3rd Qu.: 77.00   3rd Qu.: 75.00  
##  Max.   :255.00   Max.   :255.00   Max.   :255.00   Max.   :255.00  
##       X5               X6             cls           cls1        
##  Min.   :  1.00   Min.   :  1.00   land :102726   land :102318  
##  1st Qu.: 63.00   1st Qu.: 32.00   water: 20122   water: 20530  
##  Median : 89.00   Median : 60.00                                
##  Mean   : 83.18   Mean   : 59.98                                
##  3rd Qu.:112.00   3rd Qu.: 88.00                                
##  Max.   :255.00   Max.   :255.00                                
## dimension(s):
##   from  to  offset delta                     refsys point x/y
## x    1 349  288776  28.5 SIRGAS 2000 / UTM zone 25S FALSE [x]
## y    1 352 9120761 -28.5 SIRGAS 2000 / UTM zone 25S FALSE [y]

tr2 <- cbind(as.data.frame(trn), st_coordinates(trn)) |> 
  transmute(X, Y, X2=X^2, Y2=Y^2, XY=X*Y, X1, X2, X3, X4, X5, X6)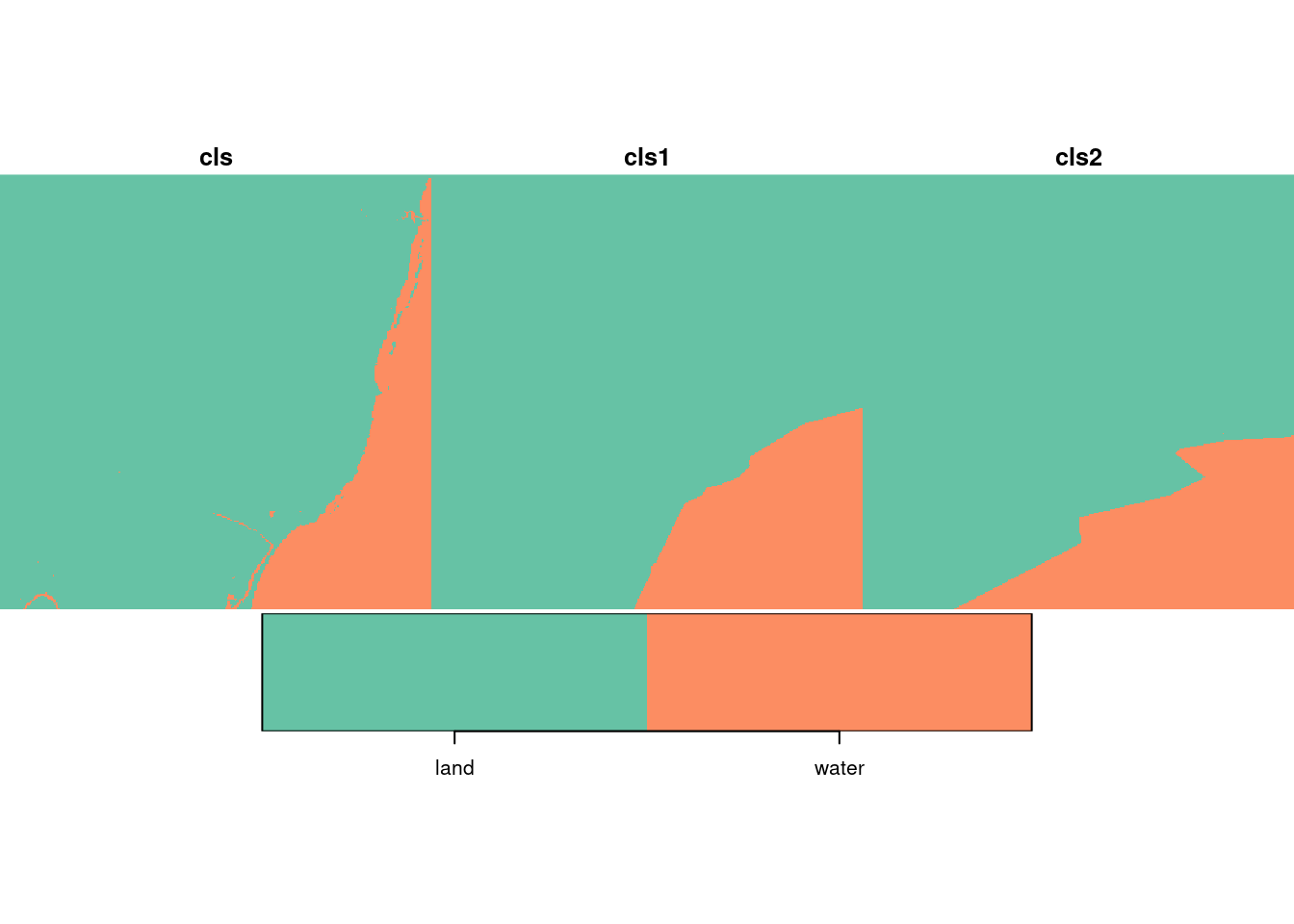

test2 <- as.data.frame(rs) |> 
  transmute(X=x, Y=y, X2=X^2, Y2=Y^2, XY=X*Y, X1, X2, X3, X4, X5, X6)

rs$cls2 = knn(tr2, test2, trn$cl, k = 5)

rs[c("cls", "cls1", "cls2")] |> merge() |> plot()

Soultions: https://edzer.github.io/sdsr_exercises/