14.11 Higher-Order Neighbors

If we wish to create an object showing to neighbours, where \(i\) is a neighbour of \(j\), and \(j\) in turn is a neighbour of \(k\), so taking two steps on the neighbour graph, we can use nblag (automatically removes \(i\) to \(i\) self-neighbours)

nb_q |> nblag(2) -> nb_q2

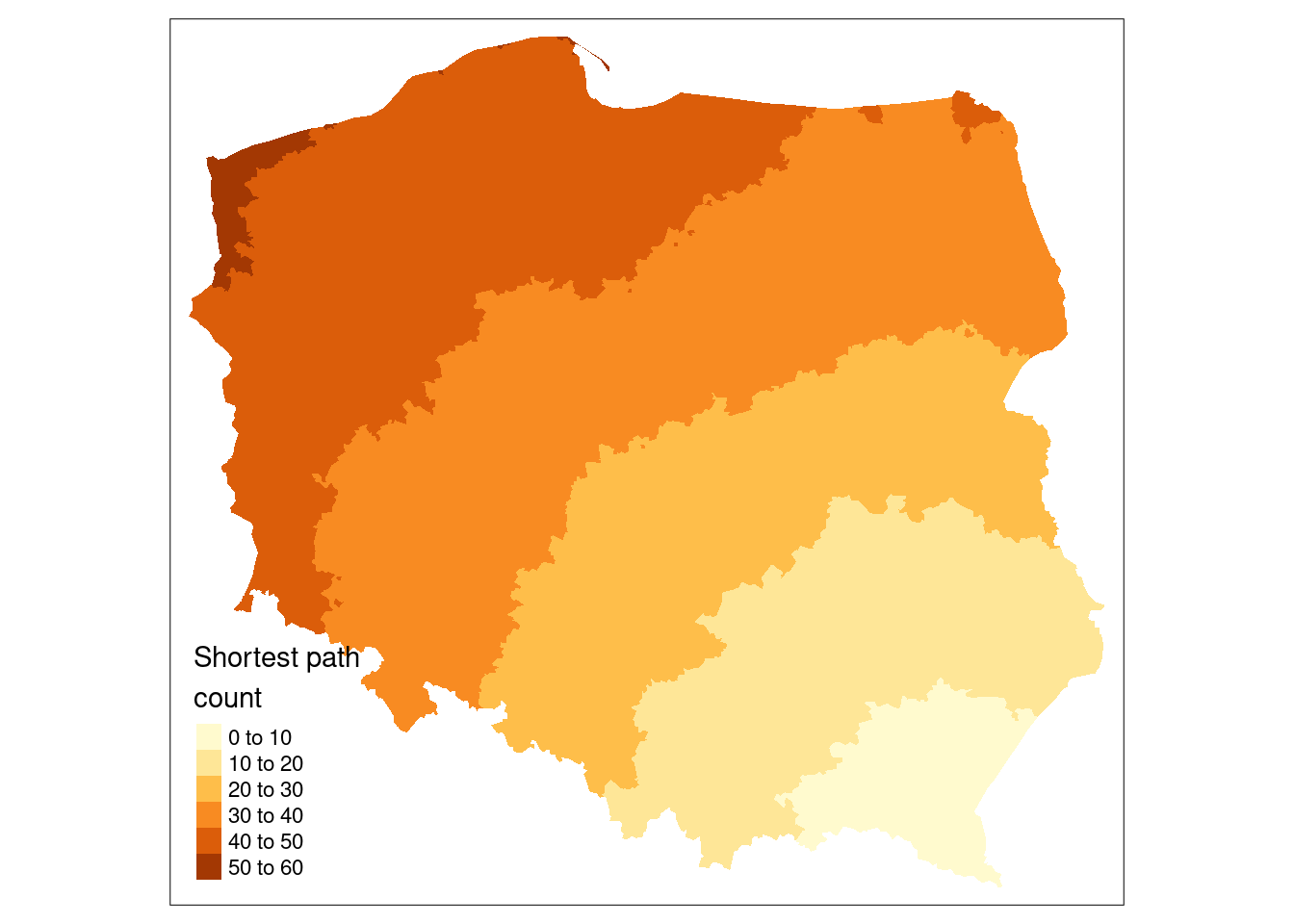
Returning to the graph representation of the same neighbour object, we can ask how many steps might be needed to traverse the graph?

igraph::diameter(g1) #where g1 is a graph object

## [1] 52

We step out from each observation across the graph to establish the number of steps needed to reach each other observation by the shortest path (creating an \(n \times n\) matrix sps), once again finding the same maximum count.

g1 |> shortest.paths() -> sps

## Warning: `shortest.paths()` was deprecated in igraph 2.0.0.
## ℹ Please use `distances()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

sps |> apply(2, max) -> spmax

spmax |> max()

## [1] 52

The municipality with the maximum count is called Lutowiska, close to the Ukrainian border in the far south east of the country.

mr <- which.max(spmax)
pol_pres15$name0[mr]

## [1] "Lutowiska"

pol_pres15$sps1 <- sps[,mr]
tm_shape(pol_pres15) +
          tm_fill("sps1", title = "Shortest path\ncount")