Using fake data simulation to understand residual plots

Why do we plot residuals vs fitted values rather then observed values?

scores <- 
  "data/gradesW4315.dat" %>% 
  read.table(header = TRUE) %>% 
  as_tibble()

scores

## # A tibble: 52 × 9
##      hw1   hw2   hw3   hw4 midterm   hw5   hw6   hw7 final
##    <int> <int> <int> <int>   <int> <int> <int> <int> <int>
##  1    95    88   100    95      80    96    99     0   103
##  2     0    74    74     0      53    83    97     0    79
##  3   100     0   105   100      91    96   100    96   122
##  4     0    90    76   100      63    91    95     0    78
##  5   100    96    99   100      91    93   100    92   135
##  6    90    83    95   100      73    89   100    90   117
##  7    95    98   100   100      59    98    98    94   135
##  8    80   100    97   100      69    94    98   101   123
##  9    95    90    98    90      78    95    99   100   109
## 10    90    94    95    98      91    94   100    89   126
## # ℹ 42 more rows

set.seed(733)
fit <- stan_glm(final ~ midterm, data = scores, refresh = 0)
fit

## stan_glm
##  family:       gaussian [identity]
##  formula:      final ~ midterm
##  observations: 52
##  predictors:   2
## ------
##             Median MAD_SD
## (Intercept) 64.2   17.7  
## midterm      0.7    0.2  
## 
## Auxiliary parameter(s):
##       Median MAD_SD
## sigma 14.9    1.6  
## 
## ------
## * For help interpreting the printed output see ?print.stanreg
## * For info on the priors used see ?prior_summary.stanreg

Predicted values and residuals.

v <- 
  scores %>% 
  mutate(
    pred = predict(fit),
    resid = residuals(fit)
  )

Residual vs. observed value.

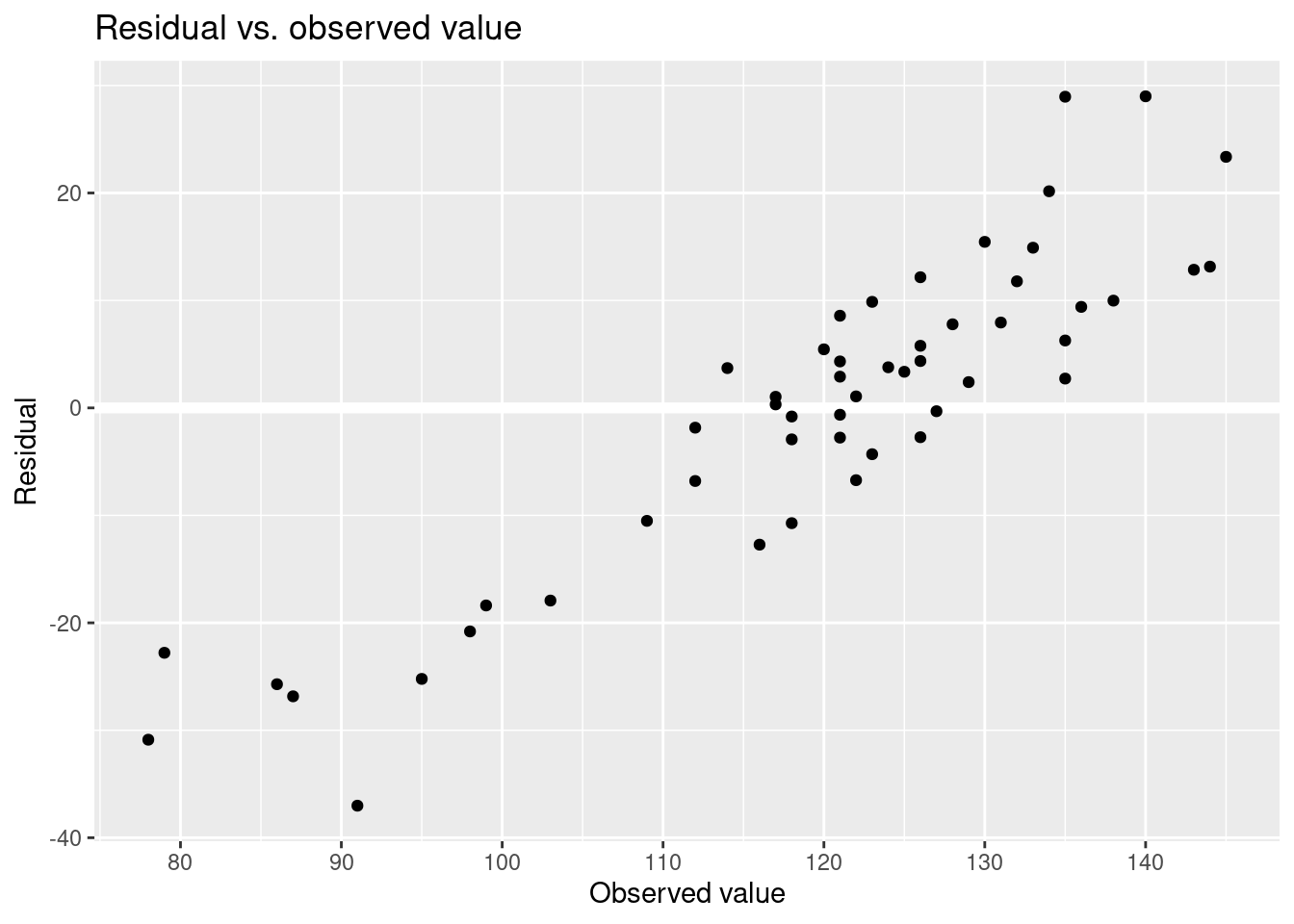
Residual vs. predicted value.

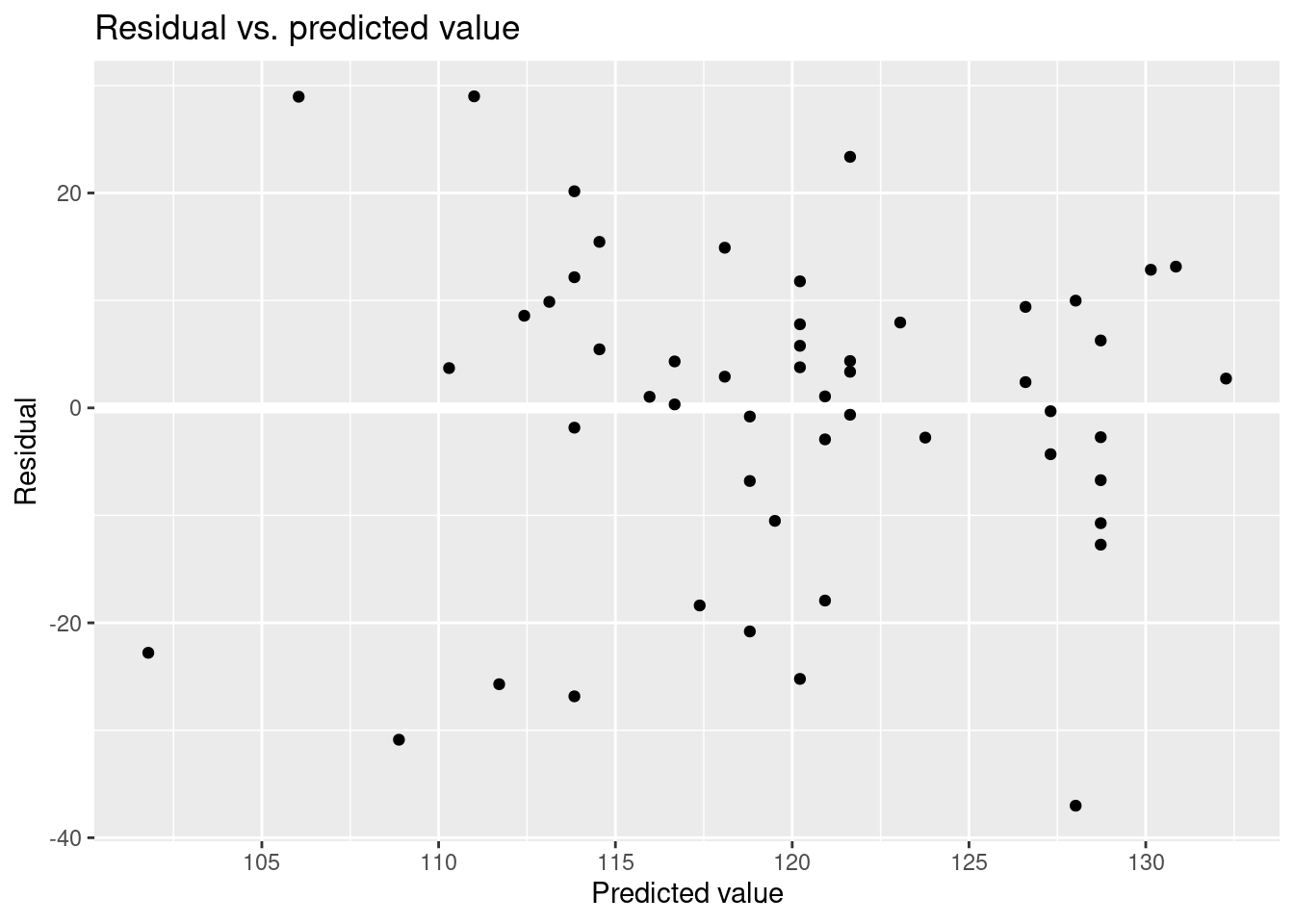
Understanding the choice using fake-data

set.seed(746)

intercept <- coef(fit)[["(Intercept)"]]
slope <- coef(fit)[["midterm"]]
sigma <- sigma(fit)

scores_sim <- 
  scores %>% 
  mutate(
    pred = intercept + slope * midterm,
    final_sim = pred + rnorm(n(), mean = 0, sd = sigma),
    resid = final_sim - pred
  )

Residual vs. observed value.

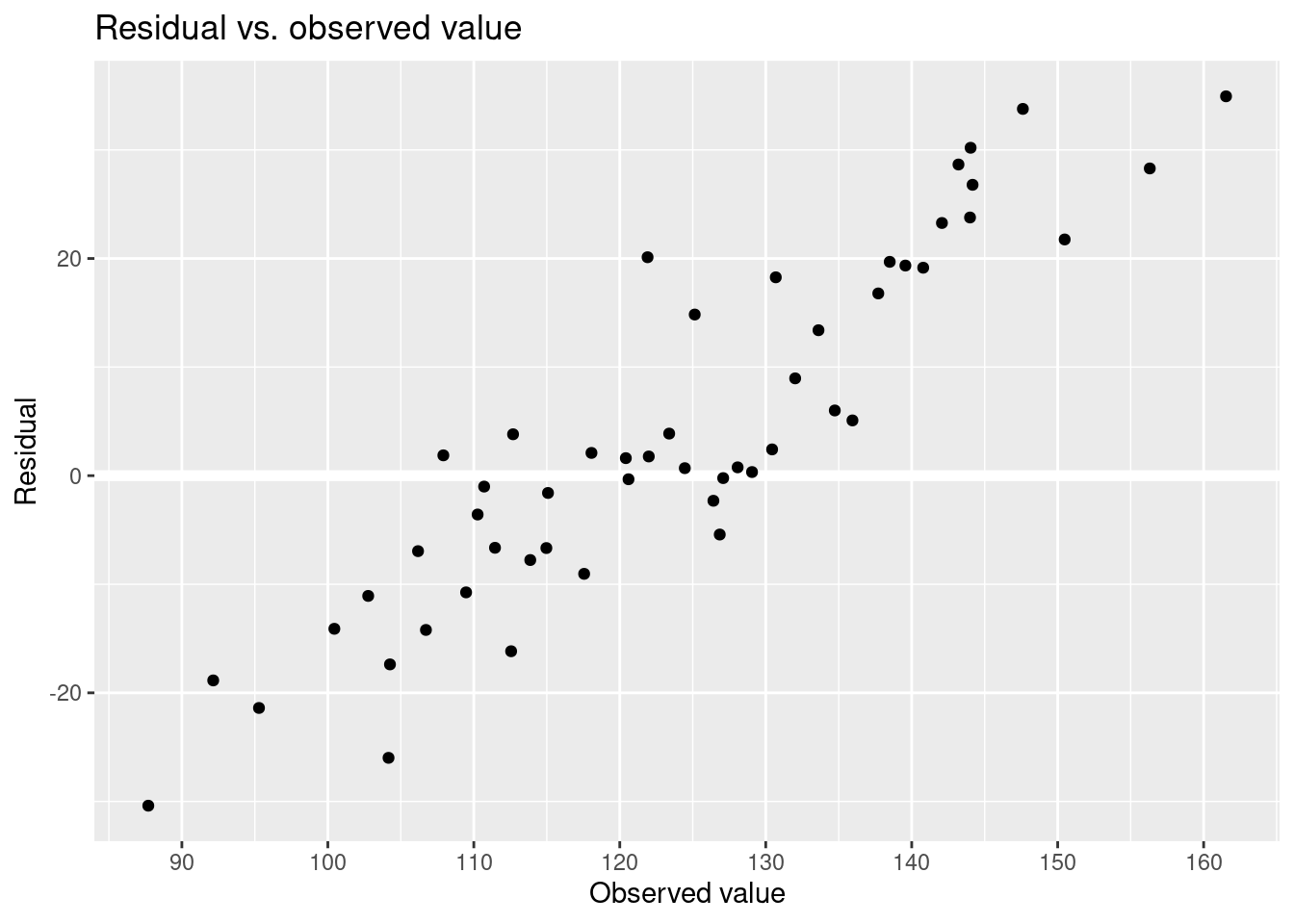
Residual vs. predicted value.

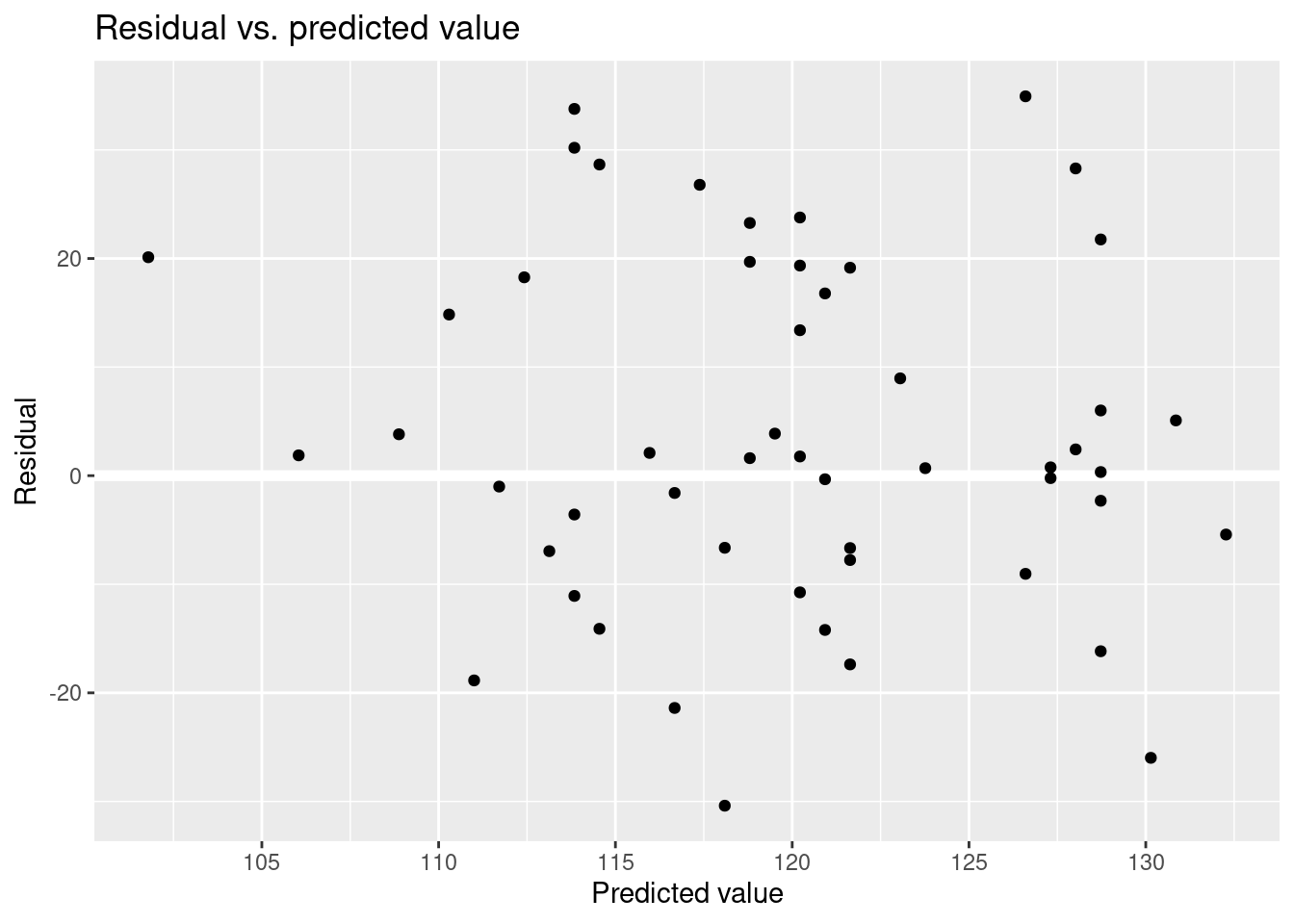
These are the type of plots you would see even if the model were correct.