11.6 Residual standard deviation \(\sigma\) and explained variance \(R^2\)
\(\sigma\) = residual standard deviation.
\(R^2\) = fraction of variance explained by the model:
\[ R^2 = 1 - \left(\sigma^2/s_y^2\right) \]
- For least squares, can compute \(R^2\) directing from ‘explained variance’:
\[ R^2 = V_{i=1}^n \hat{y}_i/s_y^2 \]
Where the \(V\) operator capture the sample variance. I.e. this is the ratio of the variance in fitted outcome values to the variance in the unfitted outcome values.
11.6.1 Bayesian \(R^2\)
Bayesian inference is not least squares, so the two formulas given previously can disagree. (Influence of the prior.)
Bayesian inference includes additional uncertainty beyond the point estimate that should be included
This leads to an alternative definition of \(R^2\) for each posterior draw \(s\):
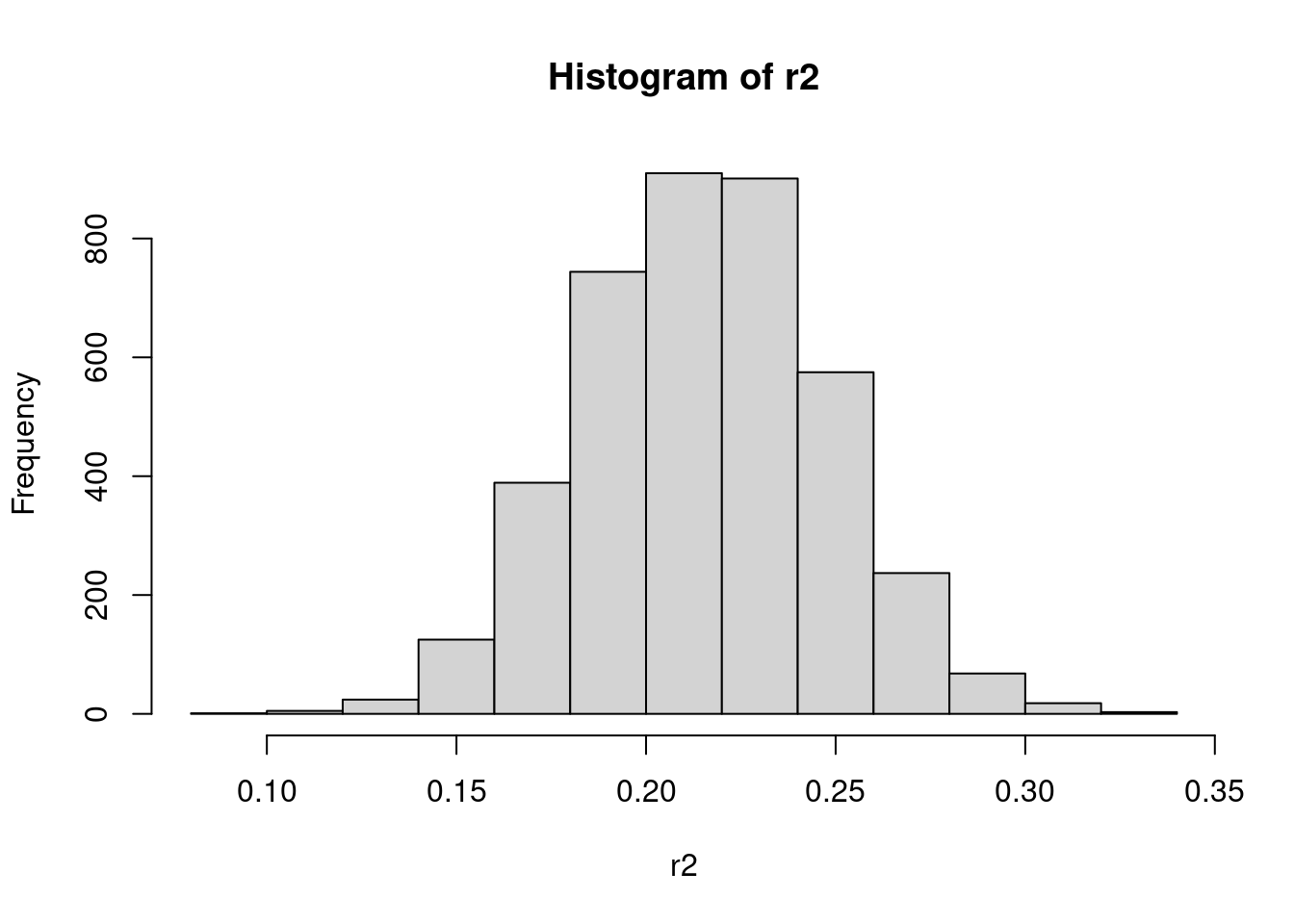
\[ \text{Bayesian } R_s^2= \frac{V_{i=1}^n \hat{y}_i^s}{V_{i=1}^n \hat{y}_i^s + \sigma_s^2} \]
This can computed in R using bayes_R2(fit). This will give draws of \(R^2\) which expresses also the uncertainty in \(R^2\).
For example for the model predicting child’s test score from given mothers score on IQ and mother’s high school status:
fit_iq <- stan_glm(kid_score ~ mom_hs + mom_iq, data = kidiq, refresh=0)
r2 <- bayes_R2(fit_iq)
hist(r2)